初中数学6.3 实数授课ppt课件

这是一份初中数学6.3 实数授课ppt课件，共22页。PPT课件主要包含了不存在，1按定义分，含开方开不尽的数，有规律但不循环的小数，含有π的数，负实数，正实数，正有理数，负有理数，2按性质分等内容，欢迎下载使用。

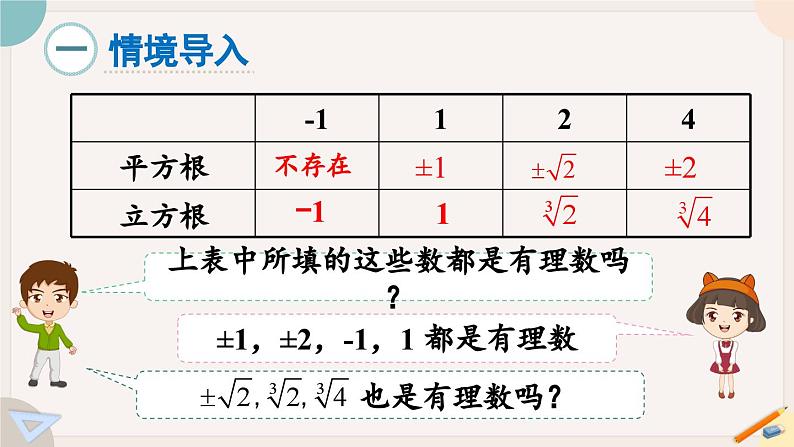
上表中所填的这些数都是有理数吗？
±1，±2，-1，1 都是有理数
事实上，任何一个有理数都可以写成有限小数或无限循环小数.
反过来，任何有限小数或无限循环小数也都是有理数.
你能举出一些无理数吗？
0.1010010001…〔两个1之间依次多1个0〕，
－168.3232232223…〔两个3之间依次多1个2〕.
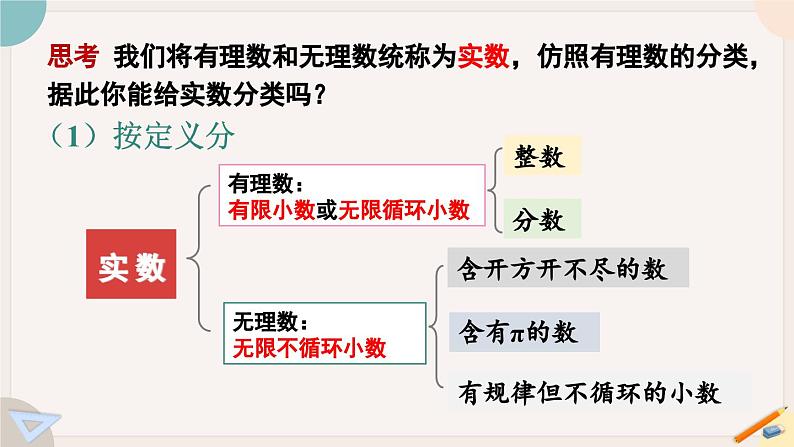
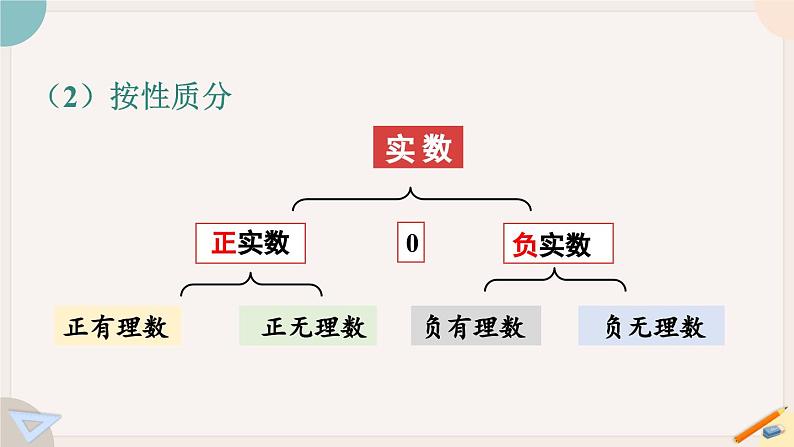
思考 我们将有理数和无理数统称为实数，仿照有理数的分类，据此你能给实数分类吗？
无理数：无限不循环小数
有理数：有限小数或无限循环小数
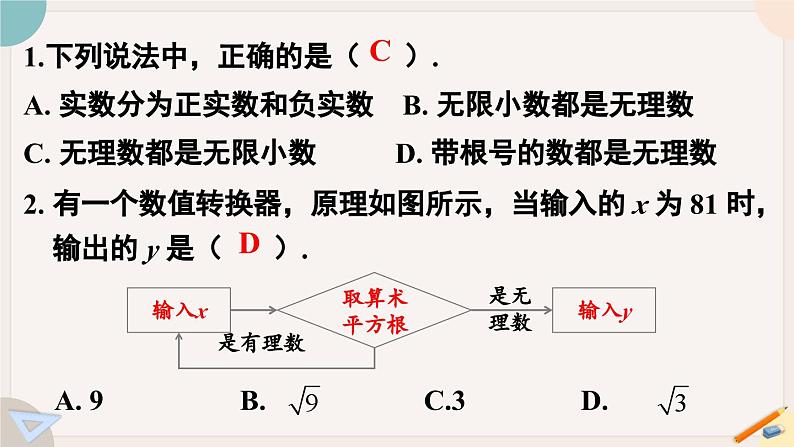
1.下列说法中，正确的是（ ）.A. 实数分为正实数和负实数 B. 无限小数都是无理数C. 无理数都是无限小数 D. 带根号的数都是无理数
2. 有一个数值转换器，原理如图所示，当输入的 x 为 81 时， 输出的 y 是（ ）.
A. 9 B. C.3 D.
问题1 每个有理数都可以用数轴上的点来表示，无理 数是否也能用数轴上的点表示出来呢？
探究 能不能在数轴上找的表示 π 的点呢？

（2）如果将所有有理数都标到数轴上，那么数轴能填满吗？
在数轴上表示的两个实数，右边的数总比左边的数大.
数轴上的点有些表示有理数，有些表示无理数.
每一个实数都可以用数轴上的一个点来表示；
反过来，数轴上的每一点都表示一个实数.
★ 实数和数轴上的点是一一对应的.
解：∵数轴上A，B两点表示的数分别为-1和 ，∴点B到点A的距离为1＋ ，则点C到点A的距离为1+ ，设点C表示的实数为x，则点A到点C的距离为-1-x，∴−1−x=1+ ，∴x=−2−
求数轴上的点表示的实数值
与有理数一样，实数也可以比较大小：
与有理数规定的大小一样，数轴上右边的点表示的实数比左边的点表示的实数大.
正数大于零，负数小于零，正数大于负数.
与有理数一样，在实数范围内：
在数轴上表示下列各点，比较它们的大小， 并用“<”连接它们.
1. 下列说法正确的是( ) A. a 一定是正实数 B. 是有理数 C. 是有理数 D. 数轴上任一点都对应一个有理数
2. 有一个数值转换器，原理如下，当输x=81时，输出 的y是( )
4. 把下列各数填入相应的括号内：
（1）有理数：{
5. 观察下图，每个小正方形的边长均为1.（1）图中阴影部分(正方形)的面积是多少？ 他的边长是多少？（2）阴影部分(正方形)的边长在哪两个整数之间？
解：(1) 阴影部分的面积为 33 - 4× ×1×2 = 9 - 4 = 5. 它的边长为 (2) 因为 5 在 4 与 9 之间，所以 在 2 与 3 之间. 即阴影部分的边长在 2 与 3 之间.
___________
有限小数或__________
1.从课后习题中选取；2.完成练习册本课时的习题。