初中人教版9.2 一元一次不等式课文ppt课件

这是一份初中人教版9.2 一元一次不等式课文ppt课件，共19页。PPT课件主要包含了实际问题，设未知数，列出方程，检验解的合理性，解方程，找等量关系，解得x≤12，去分母得，移项合并同类项得，找出不等关系等内容，欢迎下载使用。

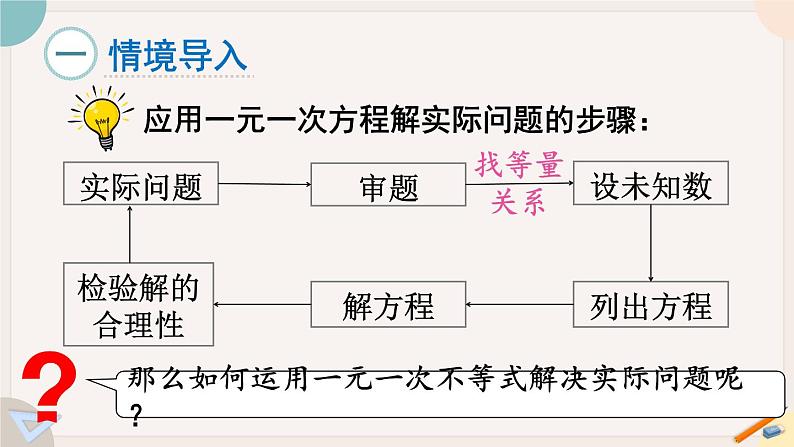
应用一元一次方程解实际问题的步骤：
那么如何运用一元一次不等式解决实际问题呢？
小华打算在星期天与同学去登山，计划上午7点出发，到达山顶后休息2h，下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h，回来时的平均速度是4km/h，他们最远能登上哪座山顶（图中数字表示出发点到山顶的路程）？
前面问题中涉及的数量关系是：
他们在山顶休息了2 h，上午7点到下午4点之间总共相隔9 h，即所用时间应小于或等于9 h.
因此要满足下午4点以前必须返回出发点，小华他们最远能登上D山顶.
（1）审：认真审题，分清已知量、未知量；（2）找：要抓住题中的关键字找出题中的不等关系；（3）设：设出适当的未知数；（4）列：根据题中的不等关系列出不等式；（5）解：解出所列不等式的解集；（6）答：检验是否符合题意，写出答案．
例 去年某市空气质量良好（二级以上）的天数与全 年天数（365）之比达到 60%，如果明年（365天） 这样的比值要超过 70%，那么明年空气质量良好的 天数要比去年至少增加多少？
一元一次不等式的实际应用
解：设明年比去年空气质量良好的天数增加了 x.
去年有 365×60% 天空气质量良好，则明年有（x+365×60%）天空气质量良好，则有：
由 x 应为正整数得：
答：明年空气质量良好的天数要比去年至少增加 37 天.
甲、乙两商场以同样价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90％收费；在乙商场累计购物超过50元后，超出50元的部分按95％收费．顾客到哪家商场购物花费少？
一元一次不等式解答费用问题
在甲商场购物超过100元后享受优惠，在乙商场购物超过50 元后享受优惠.因此，我们需要分三种情况讨论：（1）累计购物不超过50元；（2）累计购物超过50而不超过100元；（3）累计购物超过100元.
①若在甲超市花费少，则100+0.9(x-100)<50+0.95(x-50)， 得x>150 ．
②若在乙超市花费少，则100+0.9(x-100)>50+0.95(x-50)， 得x<150 ．
③若在甲乙超市花费一样，则100+0.9(x-100)=50+0.95(x-50)， 得x=150 ．
答：购物不超过50元和刚好是150元时，在两家商场购物没有 区别；超过50元而不到150元时在乙商场购物花费少；超 过150元后，在甲商场购物花费少．
（3）累计购物超过100元时
应用一元一次不等式解决实际问题的步骤：
1. 某商品原价500元，出售时标价为900元，要保持利 润不低于26%，则最低可打( ) A.六折 B. 七折 C. 八折 D. 九折
2. 某次知识竞赛共20道题，每一题答对得10分，答 错或不答都扣5分，小英得分不低于90分. 设她答 对了x道题，则根据题意可列出不等式为( ) A. 10x－5(20－x)≥90 B. 10x－5(20－x)＞90 C. 10x－(20－x)≥90 D. 10x－(20－x)＞90
3. 小明家的客厅长 5 m，宽 4 m. 现在想购买边长为 60 cm 的正方形地板砖把地面铺满，至少需要购买 多少块这样的地板砖？
4.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后，计划发生变化，准备提前2天完成修路任务，以后几天内平均每天至少要修路多少？
解：设以后几天内平均每天要修路x km，由题意得1.2+(10-2-2)x≥6. 解得 x≥0.8. 即以后几天内平均每天至少要修路0.8 km．
结果正误及是否符合题意
1.从课后习题中选取；2.完成练习册本课时的习题。