浙教版-2023年七年级上册数学举一反三系列 专题7.7 期中真题重组卷（考查范围：第1~4章）（学生版+教师版）

这是一份浙教版-2023年七年级上册数学举一反三系列 专题7.7 期中真题重组卷（考查范围：第1~4章）（学生版+教师版），文件包含专题77期中真题重组卷考查范围第14章教师版-2023年七年级上册数学举一反三系列浙教版docx、专题77期中真题重组卷考查范围第14章学生版-2023年七年级上册数学举一反三系列浙教版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

【浙教版】
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）（2022·河北唐山·八年级期中） 的立方根是 （ ）
A．2B．2C．8D．-8
【答案】A
【详解】先根据算术平方根的意义，求得=8，然后根据立方根的意义，求得其立方根为2.
故选A.
2．（3分）（2022·湖北·武汉市新洲区阳逻街第一初级中学七年级期中）下列说法：①符号相反的数互为相反数；②两个四次多项式的和一定是四次多项式；③若abc＞0，则的值为3或﹣1；④如果a大于b，那么a的倒数小于b的倒数；⑤若a3＋b3＝0，则a、b互为相反数．其中正确的个数有（ ）
A．4个B．3个C．2个D．1个
【答案】C
【分析】①根据相反数的定义即可判断；②举出反例可即可判断；③根据abc＞0分类讨论，计算出式子的值即可判断；④举出反例，即可判断；⑤根据题意，可以判断a、b的关系，即可判断．
【详解】解：只有符号不同的两个数互为相反数，故①错误；
两个四次多项式的和不一定是四次多项式，如x4+1与﹣x4﹣1的和为0，故②错误；
若abc＞0，则一正两负或三正，
当a、b、c为一正两负时，不妨设a＞0，b＜0，c＜0，则＝1+（﹣1）+（﹣1）＝﹣1；
当a、b、c为三正时，不妨设a＞0，b＞0，c＞0，则＝1+1+1＝3；故③正确；
如果a大于b，那么a的倒数不一定小于b的倒数，如a＝1，b＝﹣1，则a的倒数大于b的倒数，故④错误；
若a3+b3＝0，则a、b互为相反数，故⑤正确．
则正确的有2个．
故选：C．
【点睛】本题主要考查了整式的加减、相反数、绝对值、倒数等知识点，解答本题的关键是灵活运用相关定义和性质．
3．（3分）（2022·河南安阳·七年级期中）下列说法正确的是（ ）
A．精确到千分位B．精确到千分位
C．万精确到个位D．精确到百分位
【答案】A
【分析】根据近似数的精确度分别进行判断，即可得出答案．
【详解】解：A、精确到千分位，故本选项正确；
B、3.079×104精确到十位，故本选项错误；
C、38万精确到万位，故本选项错误；
D、精确到千分位，故本选项错误；
故选：A．
【点睛】本题考查了近似数：经过四舍五入得到的数叫近似数．
4．（3分）（2022·山东德州·七年级期中）若，，且的绝对值与相反数相等，则的值是（ ）
A．B．C．或D．2或6
【答案】C
【分析】求出a、b的值，进行计算即可．
【详解】解：∵，，
∴，，
∵的绝对值与相反数相等，
∴＜0，
∴，，
或，
故选：C．
【点睛】本题考查了绝对值的意义和有理数的计算，解题关键是理解绝对值的意义，确定a、b的值．
5．（3分）（2022·浙江·瑞安市塘下镇罗凤中学七年级期中）一列数， ， ，…… ，其中=﹣1， =， =，……， =，则×××…×=（ ）
A．1B．-1C．2017D．-2017
【答案】B
【详解】因为=﹣1,所以=,=,=,通过观察可得:,,,……的值按照﹣1,,三个数值为一周期循环,将2017除以3可得672余1,所以的值是第673个周期中第一个数值﹣1,因为每个周期三个数值的乘积为:
,所以×××…×=故选B.
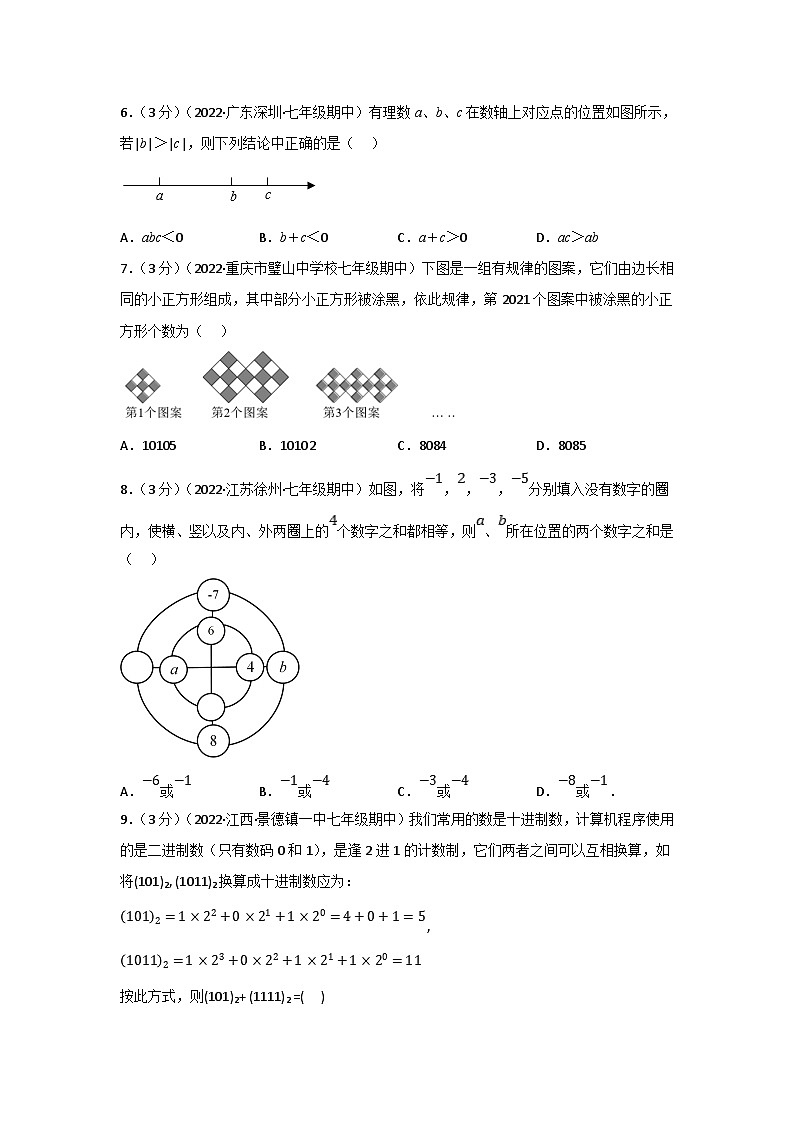
6．（3分）（2022·广东深圳·七年级期中）有理数a、b、c在数轴上对应点的位置如图所示，若|b|＞|c|，则下列结论中正确的是（ ）
A．abc＜0B．b＋c＜0C．a＋c＞0D．ac＞ab
【答案】B
【分析】根据题意，a和b是负数，但是c的正负不确定，根据有理数加减乘除运算法则讨论式子的正负．
【详解】解：∵，
∴数轴的原点应该在表示b的点和表示c的点的中点的右边，
∴c有可能是正数也有可能是负数，a和b是负数，
，但是的符号不能确定，故A错误；
若b和c都是负数，则，若b是负数，c是正数，且，则，故B正确；
若a和c都是负数，则，若a是正数，c是负数，且，则，故C错误；
若b是负数，c是正数，则，故D错误．
故选：B．
【点睛】本题考查数轴和有理数的加减乘除运算法则，解题的关键是通过有理数加减乘除运算法则判断式子的正负．
7．（3分）（2022·重庆市璧山中学校七年级期中）下图是一组有规律的图案，它们由边长相同的小正方形组成，其中部分小正方形被涂黑，依此规律，第2021个图案中被涂黑的小正方形个数为（ ）

A．10105B．10102C．8084D．8085
【答案】D
【分析】根据规律可以发现第n个图案中会有个被涂黑的小正方形．
【详解】解：第1个图案有个被涂黑的小正方形
第2个图案有个被涂黑的小正方形
第3个图案有个被涂黑的小正方形
第n个图案有个被涂黑的小正方形
所以，第2021个图案有个被涂黑的小正方形，
故选：D．
【点睛】本题考查了规律探究归纳，用代数式表示出变化规律是解题关键．
8．（3分）（2022·江苏徐州·七年级期中）如图，将，，，分别填入没有数字的圈内，使横、竖以及内、外两圈上的个数字之和都相等，则、所在位置的两个数字之和是（ ）
A．或B．或C．或D．或．
【答案】B
【分析】由于八个数的和是4，所以需满足两个圈的和是2，横、竖的和也是2，据此分步分析，列等式求解即可得到结论．
【详解】解：如图示：
设外圈上的数为，内圈上的数为，
根据题意可知，这8个数分别是、2、、4、、6、、8，
横、竖以及内外两圈上的 4 个数字之和都相等，，
内、外两圈上的 4 个数字的和是 2，横、竖的 4 个数字的和也是 2，
由，得，
由，，得，
由，，得，
则：当 时，，符合题意，此时；
当 时，，符合题意，此时，
故选：B．
【点睛】本题考查了有理数的加法，数字类题目的分析，分步分析解题的能力，读懂题意，能对题目进行分析，得到横竖两个圈的和都是2，是解决本题的关键．
9．（3分）（2022·江西·景德镇一中七年级期中）我们常用的数是十进制数，计算机程序使用的是二进制数（只有数码0和1），是逢2进1的计数制，它们两者之间可以互相换算，如将(101)2, (1011)2换算成十进制数应为：
,
按此方式，则(101)2+ (1111)2 =( )
A．(10000)2B．(10101)2C．(1011111)2D．(10100)2
【答案】D
【分析】根据例子可知：若二进制的数有n位，那么换成十进制，等于每一个数位上的数乘以2的（n-1）方，再相加即可，先把式子化成十进制数，然后再求和，把求和得到的数再转化成二进制数即可．
【详解】解： (101)2+ (1111)2 =5+15=20，
20=16+4==，
故选：D．
【点睛】本题主要考查有理数的混合运算，解题关键在于理解自我十进制，二进制互相转化的方法．
10．（3分）（2022·河北唐山·七年级期中）某水果店在甲批发市场以每箱a元的价格购进了20箱大枣，又在乙批发市场以每箱b元（bA．盈利了10a元B．亏损了10b元
C．盈利了元D．亏损了10（a-b）元
【答案】C
【分析】根据题意可以计算出售价与成本的差值，然后根据b＜a，即可解答本题．
【详解】解：∵
=30a+30b-20a-40b
=10a-10b
=10(a-b)，
又∵b∴a-b>0，
∴10(a-b)>0，
∴这家商店盈利了元，
故选：C．
【点睛】本题考查整式加减运算的应用，正负数的意义，解答本题的关键是明确题意，列出相应的代数式．
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）（2022·广东·珠海市湾仔中学七年级期中）2011年3月11日北京时间13时40分日本发生9.0级地震，造成人员伤亡和重大的经济损失；据媒体报道，截止3月17日，地震海啸灾害造成高达约1999亿美元的经济损失，用科学记数法表示1999亿美元为_____美元．
【答案】1.999×1011
【分析】绝对值大于1的数可以用科学记数法表示，一般形式为，为正整数，且比原数的整数位数少1，据此可以解答．
【详解】解：1999亿＝199900000000＝1.999×1011，
故答案为：1.999×1011．
【点睛】本题考查用科学记数法表示较大的数，熟练掌握科学记数法表示较大的数一般形式为，其中，是正整数，正确确定的值和的值是解题的关键．
12．（3分）（2022·广东广州·七年级期中）定义一种新运算：对任意有理数a，b都有，例如：，则(2021∇2)∇2=__________．
【答案】2021
【分析】读懂题意，根据新定义计算即可．
【详解】解：（3分）（2022∇2)∇2
=2021．
故答案为：2021．
【点睛】本题考查了数与式中的新定义，做题关键是读懂新定义，按照新定义计算．
13．（3分）（2022·浙江·金华市南苑中学七年级期中）已知7＋的整数部分是m，11-的小数部分是n，则m＋n＝______
【答案】
【分析】根据无理数的估算方法，先估算的大小，再确定7＋的整数部分和11-的小数部分，相加即可．
【详解】解：∵9<13<16，
∴3<<4，
∴10<7＋<11，7<11-<8，
则7＋的整数部分为10，11-的小数部分为11--7=4－，
∴m=10，n=4-，
∴m+n=10+4-=14-，
故答案为：14-．
【点睛】本题主要考查了无理数的估算，熟练掌握算术平方根的定义是解题的关键．
14．（3分）（2022·黑龙江·肇源县第五中学期中）一个两位数十位上的数字和个位上的数字交换位置后得到的新数与原数的和一定是 _________的倍数．
【答案】11
【分析】设原数的个位数字为y，十位数字为x，则原数为10x＋y，则新数为10y＋x，
表示出原数和新数，相加后合并同类项，提取公因式后可得答案．
【详解】解：设原数的个位数字为y，十位数字为x，则原数为10x＋y，则新数为10y＋x，
∵（10y＋x）＋（10x＋y）
＝10y＋x＋10x＋y
＝11x＋11y
＝11（x＋y）
∴新数与原数的和一定是11的倍数，
故答案为：11
【点睛】本题考查了两位数的表示方法、合并同类项、提公因式法进行因式分解等知识，熟练掌握两位数的表示方法是关键．
15．（3分）（2022·黑龙江·哈尔滨市第十七中学校期中）已知数轴上A、B两点表示的数互为相反数，并且两点间的距离是18，在A、B之间有一点P，若P到A的距离是P到B的距离的，则P点表示的数是___________．
【答案】
【分析】直接利用相反数的意义得出A，B表示的数，再利用P到A的距离是P到B的距离的得出PA的长度，然后分情况求解即可．
【详解】解：∵数轴上A、B表示的数互为相反数，并且两点间的距离是18，
∴A表示−9，B表示9或A表示9，B表示−9，
∵在A、B之间有一点P，P到A的距离是P到B的距离的，
∴PA＝6，PB＝12，
∴当A表示−9时，点P表示的数是－9＋6＝－3，
当A表示9时，点P表示的数是9－6＝3，
故答案为：．
【点睛】此题主要考查了数轴以及相反数的意义，正确得出点A，B的位置是解题关键．
16．（3分）（2022·黑龙江齐齐哈尔·七年级期中）数轴上表示整数的点称为整点．某数轴的单位长度是1cm，若在这个数轴上随意画出一条长为2021cm的线段AB，则盖住的整点的个数是______．
【答案】2022或2021##2021或2022
【分析】以线段AB的端点与数轴上的整点是否重合进行讨论可得结论．
【详解】解：∵数轴的单位长度是1cm，AB=2021cm，
∴若点A与一整点重合，则B点也与一整点重合，两点之间有2021个整点．
∴线段AB共盖住了2022个整点．
若点A不与整点重合，则点B也不与整点重合，两点之间有2021个整点．
综上，线段AB盖住的整点的个数为2022或2021个．
故答案为2022或2021．
【点睛】本题主要考查了数轴的应用．对于多解问题要注意分类讨论．
三．解答题（共9小题，满分72分）
17．（6分）（2022·江苏·无锡市华庄中学七年级期中）计算
(1)；
(2)；
(3)；
(4)．
【答案】(1)1
(2)
(3)
(4)32
【分析】（1）根据有理数加减计算法则求解即可；
（2）首先计算乘方、绝对值，然后计算乘法，最后计算减法，求出算式的值即可；
（3）根据乘法分配律，求出算式的值即可；
（4）首先计算乘方和中括号里面的乘方、除法和加法，然后计算中括号外面的减法，求出算式的值即可．
（1）
解：原式

；
（2）
解：原式
（3）
解：原式
；
（4）
解：原式
．
【点睛】本题主要考查了有理数的加减计算，有理数乘法分配律，含乘方的有理数混合计算，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．另外，注意乘法运算定律的应用．另外，注意乘法运算定律的应用．
18．（6分）（2022·广西·河池市宜州区教育局教学研究室七年级期中）已知2a-1的平方根为±3，3a＋b的算术平方根为4，求5a＋2b的立方根．
【答案】3
【分析】由题意可知，2a-1＝9，3a＋b＝16，求出a，b的值，最后代入计算即可．
【详解】解：∵2a-1的平方根为±3，
∴2a-1＝9，
∴a＝5，
∵3a＋b的算术平方根为4，
∴3a＋b＝16，即15＋b＝16，
∴b＝1，
∴5a＋2b＝25＋2＝27，
∴5a＋2b的立方根为3．
【点睛】本题考查了平方根和算术平方根以及立方根的定义，熟练掌握其定义是解决问题的关键．
19．（6分）（2022·湖南永州·七年级期中）已知代数式
(1)若，
①求；
②当时，求的值；
(2)若（a为常数），且A与B的和不含项，求整式的值．
【答案】(1)①；②8
(2)19
【分析】（1）根据整式的加减运算化简求值即可；
（2）根据整式的加减运算顺序即可求解；
（3）根据和中不含x2项即是此项的系数为0即可求解．
（1）① ，②由①知，当时，；
（2）， ，∵A与B的和不含项，， 即， ．
【点睛】本题考查了整式的加减，解答本题的关键是掌握多项式加减的运算法则，合并同类项的法则．
20．（8分）（2022·天津市红桥区教师发展中心七年级期中）某粮食中转站仓库在9月1日至9月10日的时间内运进、运出粮食情况如下（运进记作“+”，运出记作“－”；单位：吨）：+1050，-500，+2300，-80，-150，-320，+600，-360，+500，-210，且已知在9月1日前，仓库无粮食．
(1)求9月10日仓库内共有粮食多少吨？
(2)求哪一天仓库内的粮食最多，最多是多少？
(3)若每吨粮食的运费（包括运进、运出）10元，从9月1日至9月10日仓库共需付运费多少元？
【答案】(1)2830
(2)9月9日仓库内的粮食最多，最多是3040吨
(3)60700
【分析】（1）将记录的数字相加即可得到结果；
（2）求出1日到10日的粮食数，得出仓库内的粮食最多的天数，求出最多的数量即可；
（3）求出记录数字的绝对值之和，乘以10即可得到结果．
（1）
解：+1050-500+2300-80-150-320+600-360+500-210=2830（吨），
答：9月10日仓库内共有粮食2830吨；
（2）
解：9月1日仓库内的粮食为1050吨，
9月2日仓库内的粮食为：1050-500=550（吨），
9月3日仓库内的粮食为：550+2300=2850（吨），
9月4日仓库内的粮食为：2850-80=2770（吨），
9月5日仓库内的粮食为：2770-150=2620（吨），
9月6日仓库内的粮食为：2620-320=2300（吨），
9月7日仓库内的粮食为：2300+600=2900（吨），
9月8日仓库内的粮食为：2900-360=2540（吨），
9月9日仓库内的粮食为：2540+500=3040（吨），
9月10日仓库内的粮食为：3040-210=2830（吨），
答：9月9日仓库内的粮食最多，最多是3040吨；
（3）
解：运进1050+2300+600+500=4450（吨），
运出|-500-80-150-320-360-210|=1620（吨），
10×（4450+1620）=10×6070=60700（元），
答：从9月1日到9月10日仓库共需付运费60700元．
【点睛】此题考查了正数与负数以及有理数的混合运算的应用，弄清题意是解本题的关键．
21．（8分）（2022·河北·原竞秀学校七年级期中）小明家最近刚购置了一套商品房，如图是这套商品房的平面图（阴影部分）（单位：m）．
(1)这套房子的总面积可以用式子表示为______；
(2)若，，并且房价为每平方米0.5万元，则购买这套房子共需要多少万元？
【答案】(1)
(2)59
【分析】（1）将四个长方形的面积求和即可获得答案；
（2）将x、y的值代入代数式即可求得这套房子的总面积，然后乘以0.5即为房子的总价．
（1）
解：这套房子的总面积用式子表示为．
故答案为：；
（2）
若，，并且房价为每平方米0.5万元，
则万元，
即购买这套房子共需要59万元．
【点睛】本题主要考查了列代数式和代数式求值，理解题意，正确列出代数式是解题关键．
22．（9分）（2022·河北唐山·七年级期中）某学校为了全面提高学生的综合素养，组织了音乐，朗诵，舞蹈，美术共四个社团，学生积极参加（每个学生限报一项），参加社团的学生共有（6x-2y）人，其中音乐社团有x人参加，朗诵社团的人数比音乐社团的人数的两倍少y人，舞蹈社团的人数比朗诵社团人数一半多2人．
(1)求参加朗诵社团有多少人；（用含x，y的式子表示）
(2)求朗诵社团比舞蹈社团多多少人？（用含x，y的式子表示）
(3)若，，求美术社团的人数．
【答案】(1)参加朗诵社团有（2x-y）人
(2)朗诵社团比舞蹈社团多人
(3)美术社团的人数为106人
【分析】（1）根据朗诵社团与音乐社团的人数的等量关系可得答案；
（2）根据舞蹈社团与朗诵社团的人数的等量关系，求出参加舞蹈社团的人数，再根据整式的减法法则可得答案；
（3）先根据整式的加减运算法则，用x、y表示出参加美术社团的人数，再将x、y的值代入计算即可．
（1）
解：∵音乐社团有x人参加，朗诵社团的人数比音乐社团的人数的两倍少y人，
∴参加朗诵社团有（2x-y）人；
（2）
∵舞蹈社团的人数比朗诵社团人数一半多2人，
∴舞蹈社团的人数为=人，
∴，
∴朗诵社团比舞蹈社团多人；
（3）
∵参加美术社团的人数为人，
∴当，时，
，
∴参加美术社团的人数为106人．
【点睛】本题考查整式的加减、列代数式，明确等量关系，掌握运算法则是解题的关键．
23．（9分）（2022·河南洛阳·七年级期中）先阅读内容，然后解答问题：
因为：
所以：＝
＝1﹣
＝1﹣
问题：（1）请你猜想（化为两个数的差）：＝ ；＝ ；
（2）若a、b为有理数，且|a﹣1|+（ab﹣2）2＝0，求+…+的值．
【答案】（1），；（2）.
【分析】（1）根据题目中式子的特点可以写出猜想；
（2）根据|a-1|+（ab-2）2=0，可以取得a、b的值，代入然后由规律对数进行拆分，从而可以求得所求式子的值．
【详解】解：（1），
，
故答案为：，；
（2）∵|a﹣1|+（ab﹣2）2＝0，
∴a﹣1＝0，ab﹣2＝0，
解得，a＝1，b＝2，
∴
=
＝1﹣
＝1﹣
＝．
【点睛】本题考查数字的变化类、非负数的性质、有理数的混合运算，解答本题的关键是明确题意，求出所求式子的值．
24．（10分）（2022·湖北武汉·七年级期中）把正整数1，2，3，…，2021排成如图所示的7列，规定从上到下依次为第1行，第2行，第3行，…，从左到右依次为第1列至第7列．
(1)数2021在第 行，第 列．
(2)按如图所示的方法，用正方形方框框住相邻的四个数，设被框住的四个数中，最小的一个数为x，那么：
①被框住的四个数的和等于 ；（用含x的代数式表示）
②被框住的四个数的和是否可以等于816或2816？若能，则求出x的值；若不能，则说明理由．
(3)（直接填空）设从第1列至第7列各列所有数的和依次记为S1，S2，S3，…，S7，那么
①S1，S2，S3，…，S7这7个数中，最大数与最小数的差等于 ．
②从S1，S2，S3，…，S7中挑选三个数，写出一个等式表达所选三个数之间的等量关系，你写出的等式是 （写出一个即可）．
【答案】(1)289，5
(2)①4x+16；②被框住的四个数的和可以等于816，此时x＝200，而不能等于2816，理由见解析
(3)①1733；②S1+S3＝2S2（答案不唯一），
【分析】（ 1）求出2021÷7的商和余数即可求解；
（2 ）①根据另3个数与最小的数相隔1，7，8，可得相应的代数式，相加可得这4个数的和；
②把816或2816代入（ 2）①得到的四个数的和中的代数式，计算可得x的值；
（ 3）①易得2021个数共有288行数另有5个数，则最大的数为S5，最小的数为S6，让202 S5减去S6即为最大数与最小数之差；
②根据差补法即可得其中两个数的和等于另一个数的2倍．
（1）
∵2021÷7＝288……5，
∴数2021在第289行第5列．
故答案为：289，5；
（2）
①设被框的四个数中，最小的一个数为x，那么其余三个数为x+1，x+7，x+8，
则被框的四个数的和为：x+x+1+x+7+x+8＝4x+16．
故答案为：4x+16；
②被框住的四个数的和可以等于816，此时x＝200，也可以等于2816，此时x=700，理由如下：
当4x+16＝816时，解得x＝200，
当4x+16＝2816时，解得x＝700．
∵200不是7的倍数，700是7的倍数，而最小值不能在第7列，
∴被框住的四个数的和可以等于816，此时x＝200，而不能等于700；
（3）
①∵，
，
，
，
∴，
，
∴，，
∵，
∴，
∴这7个数中最大数与最小数的差值为
．
故最大数与最小数的差等于1733．
故答案为：1733；
②S1+S3＝1289+3289+27(1+2+3+…+288)
=(1+3)289+27(1+2+3+…+288)
=2[2289+7(1+2+3+…+288)]
=2S2，
故答案为：S1+S3＝2S2，（答案不唯一）．
【点睛】本题考查了利用探究正整数排列规律列代数式式，解决问题的关键是探究正整数排列的变化是规律，按得到的规律列代数式，解答问题．
25．（10分）（2022·陕西·西安市西航二中七年级期中）已知：b是最小的正整数，且a、b满足（c﹣5）2+|a+b|＝0，请回答问题：
(1)请直接写出a、b、c的值，a＝______，b＝______，c＝______．
(2)数轴上a、b、c三个数所对应的分别为A、B、C，点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点A、B、C同时开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动．
①经过2秒后，求出点A与点C之间的距离AC．
②经过t秒后，请问：BC﹣AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．
【答案】(1)﹣1，1，5
(2)①14；②BC﹣AB的值是不随着时间t的变化而改变，其值为2
【分析】（1）根据b是最小的正整数求出b，再用绝对值和平方的非负性求出a、b的值．
（2）①用点C表示的数减去点A表示的数即可表示出AC的长．
②先表示出BC、AB，就可以得出BC-AB的值的情况．
（1）
∵b是最小的正整数，
∴b＝1．
∵，
∴，
∴a＝﹣1，b＝1，c＝5．
故答案为：﹣1，1，5；
（2）
设点A、B、C运动的时间为t秒，
由题意得：移动后点A表示的数为：﹣1﹣t，点B表示的数为：1+t，点C表示的数为：5+3t；
①AC＝5+3t﹣（﹣1﹣t）＝4t+6，
当t＝2时，AC＝8+6＝14，
故点A与点C之间的距离AC是14个单位；
②由题意，得
BC＝（5+3t）﹣（1+t）＝4+2t，AB＝（1+t）﹣（﹣1﹣t）＝2+2t，
∴BC﹣AB＝4+2t﹣（2+2t）＝2．
∴BC﹣AB的值是不随着时间t的变化而改变，其值为2．
【点睛】本题考查了数轴的应用，数轴上任意两点的距离，代数式表示数的运用，非负数的性质，解题的关键是知道数轴上任意两点间的距离公式．