2023年浙江省嘉兴市南湖区中考二模数学试题

这是一份2023年浙江省嘉兴市南湖区中考二模数学试题，共8页。
1． 全卷满分120分，考试时间120分钟． 试题卷共6页，有三大题，共24小题．
2． 全卷答案必须做在答题纸卷I、卷II的相应位置上，做在试题卷上无效．
卷I（选择题）
一、选择题（本题有10小题，每小题3分，共30分． 请选出各题中唯一的正确选项，不选、多选、错选，均不给分）
1. 若向东走米记为，则表示（ ）
A. 向西走2米B. 向东走2米C. 向西走米D. 向北走2米
2. 年卡塔尔世界杯决赛有近亿人观看，数据亿用科学记数法表示，结果为（ ）
A. B. C. D.
3. 计算的结果是（ ）
A B. C. D.
4. 神奇的自然界处处蕴含着数学知识，动物学家发现蝴蝶身长与双翅张开后的长度之比约为． 这个数据体现了数学中的（ ）

A. 平移B. 轴对称C. 旋转D. 黄金分割
5. 如图是一个“凹”字形几何体，它的左视图是（ ）

A. B. C. D.
6. 已知是实数，且，下列说法一定正确的是（ ）
A. 若，则B. 若，则
C. 若，则D. 若，则
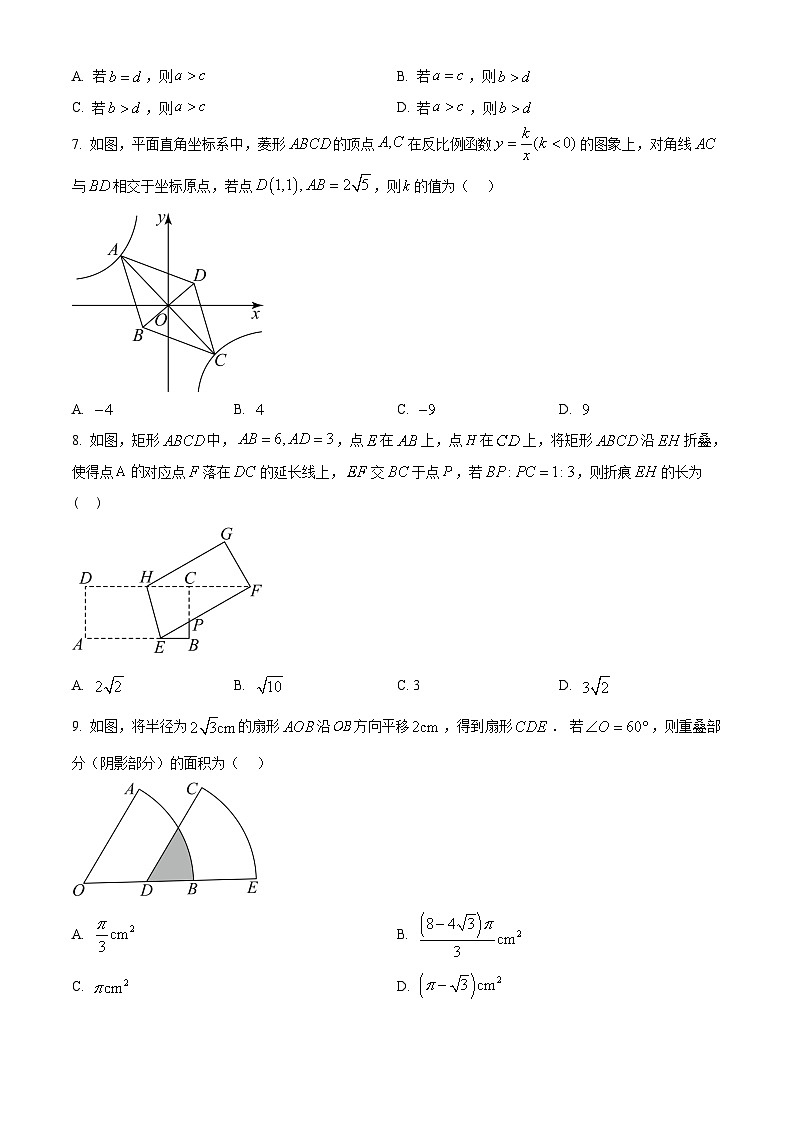
7. 如图，平面直角坐标系中，菱形的顶点在反比例函数的图象上，对角线与相交于坐标原点，若点，则的值为（ ）

A. B. C. D.
8. 如图，矩形中，，点在上，点在上，将矩形沿折叠，使得点对应点落在的延长线上，交于点，若，则折痕的长为( )

A. B. C. 3D.
9. 如图，将半径为的扇形沿方向平移，得到扇形． 若，则重叠部分（阴影部分）的面积为（ ）

A. B.
C. D.
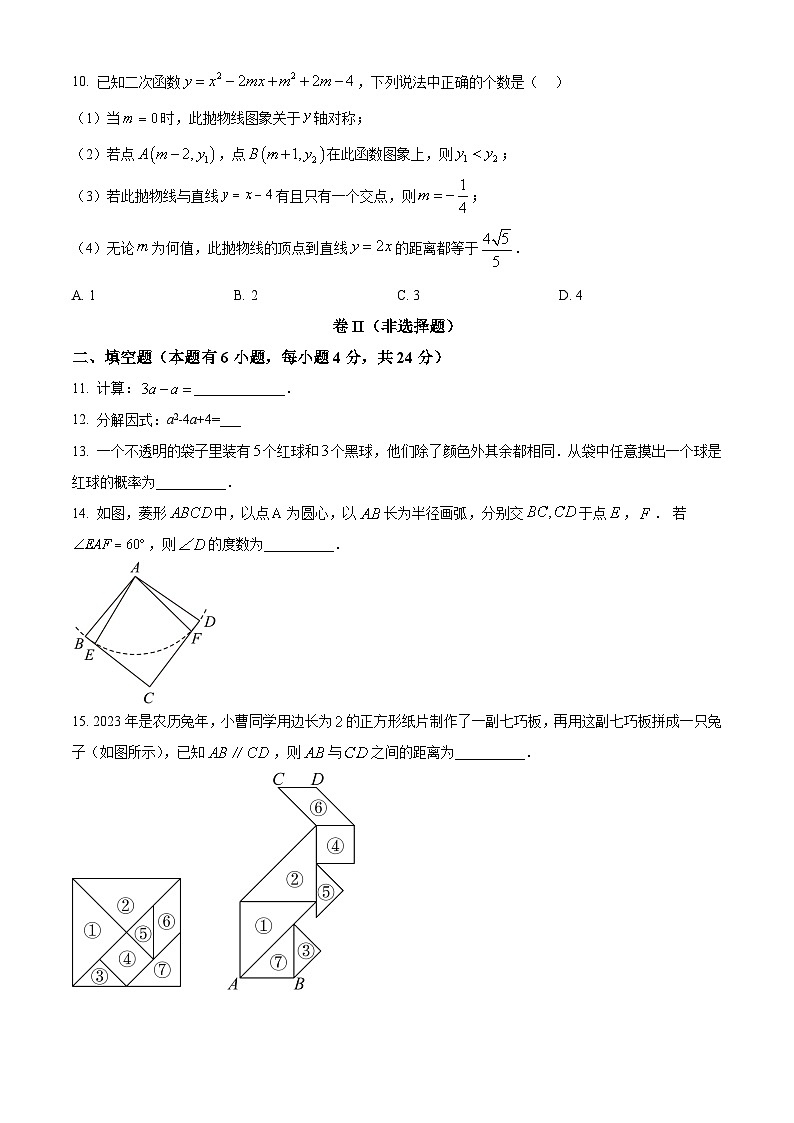
10. 已知二次函数，下列说法中正确的个数是（ ）
（1）当时，此抛物线图象关于轴对称；
（2）若点，点在此函数图象上，则；
（3）若此抛物线与直线有且只有一个交点，则；
（4）无论为何值，此抛物线的顶点到直线的距离都等于．
A. 1B. 2C. 3D. 4
卷II（非选择题）
二、填空题（本题有6小题，每小题4分，共24分）
11. 计算：_____________．
12. 分解因式：a2-4a+4=___
13. 一个不透明的袋子里装有个红球和个黑球，他们除了颜色外其余都相同．从袋中任意摸出一个球是红球的概率为__________．
14. 如图，菱形中，以点为圆心，以长为半径画弧，分别交于点，． 若，则的度数为__________．

15. 2023年是农历兔年，小曹同学用边长为的正方形纸片制作了一副七巧板，再用这副七巧板拼成一只兔子（如图所示），已知，则与之间的距离为__________．

16. 在中，，点分别是的中点，点是上的一个动点，连结，作交于点，连结． 点从点向点运动的过程中，的最小值为__________．

三、解答题（本题有8小题，第17-19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）
友情提示：做解答题，别忘了写出必要的过程；作图（包括添加辅助线）最后必须用黑色字迹的签字笔或钢笔将线条描黑．
17. （1）计算：．
（2）解方程：
18. 化简：，以下是小曹同学的解答过程． 思考并完成以下任务．
解：原式 ①
②
③
任务：
（1）小曹的解答过程是从第几步开始出错的，请指出错误的原因；
（2）请尝试写出正确的化简过程．
19. 如图是的正方形网格，请仅用无刻度的直尺按要求完成作图．

（1）在图1中的格点上找一点，使得；
（2）在图2中过点作一条直线，使点到直线的距离相等．
20. 综合与实践
【情境】在数学活动课上，周老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．
【发现】同学们随机收集香柚树、桔子树的树叶各10片，通过测量得到这些树叶的长和宽的数据后，分别计算长宽比，整理数据如下：
分析数据如下：
探究】
（1）上述表格中__________，__________；
（2）①小钱同学说：“从树叶长宽比的方差来看，我认为香柚树叶的形状差别大．”
②小曹同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现桔子树叶的长约为宽的两倍． ”
上面两位同学的说法中，合理的是__________；（填序号）
（3）现有一片长，宽的树叶，请判断这片树叶更可能来自于香柚树、桔子树中的哪种树？并给出你的理由．

21. 观察下列等式
第一个：；
第二个：
第三个：；
……
（1）尝试：__________；
（2）猜想：请用含（，且为整数）的代数式表示第个等式；
（3）验证：请你运用学过的知识证明你的猜想．
22. 为了预防近视，要求学生写字姿势应保持“一尺、一拳、一寸”，即眼睛与书本距离约为一尺（约），胸前与课桌距离约为一拳，握笔的手指与笔尖距离约为一寸． 如图，为桌面，某同学眼睛看作业本的俯角为为身体离书桌距离，眼睛到桌面的距离．

（1）通过计算，请判断这位同学的眼睛与作业本的距离是否符合要求；
（2）为确保符合要求，需将作业本沿方向移动．当眼睛看作业本的俯角为时，求作业本移动的距离．（，． 结果精确到0.1）
23. 某商家计划在抖音直播平台上直播销售当地特产，将其中一种特产在网上进行试销售．
该商家在试销售期间调查发现，每天销售量y（万件）与销售单价x（元/件）的数据如表：
（1）根据所给数据判断函数类型，并求y关于x的函数表达式；
（2）总成本P（万元）与销售量y（万件）之间存在如图所示的变化趋势，当时可看成一条线段，当时可看成抛物线
①销售量不超过万件时，利润为万元，求此时的售价为多少元/件？
②当售价为多少元时，利润最大，最大值是多少万元？（利润＝销售总额－总成本）
24. 在等边中，，点是的中点，点分别是边上一点(不与点重合)．

（1）如图1，当点为中点，点为中点时，求的长度；
（2）如图2，将线段绕着点顺时针旋转得到线段，连接，当三点在同一条直线上时，求的长度；
（3）如图3，将线段绕着点顺时针旋转得到线段，延长交线段于点，探索三条线段之间的关系．
数据 序号
类别
香柚树叶的长宽比
桔子树叶的长宽比
平均数
中位数
众数
方差
香柚树叶长宽比
桔子树叶的长宽比
x（元/件）
…
10
12
14
16
…
y（万件）
…
14
12
10
8
…