人教A版2024年高一数学寒假提高讲义 第14课 平面向量章末复习（2份打包，原卷版+教师版）

这是一份人教A版2024年高一数学寒假提高讲义 第14课 平面向量章末复习（2份打包，原卷版+教师版），文件包含人教A版2024年高一数学寒假提高讲义第14课平面向量章末复习原卷版doc、人教A版2024年高一数学寒假提高讲义第14课平面向量章末复习教师版doc等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

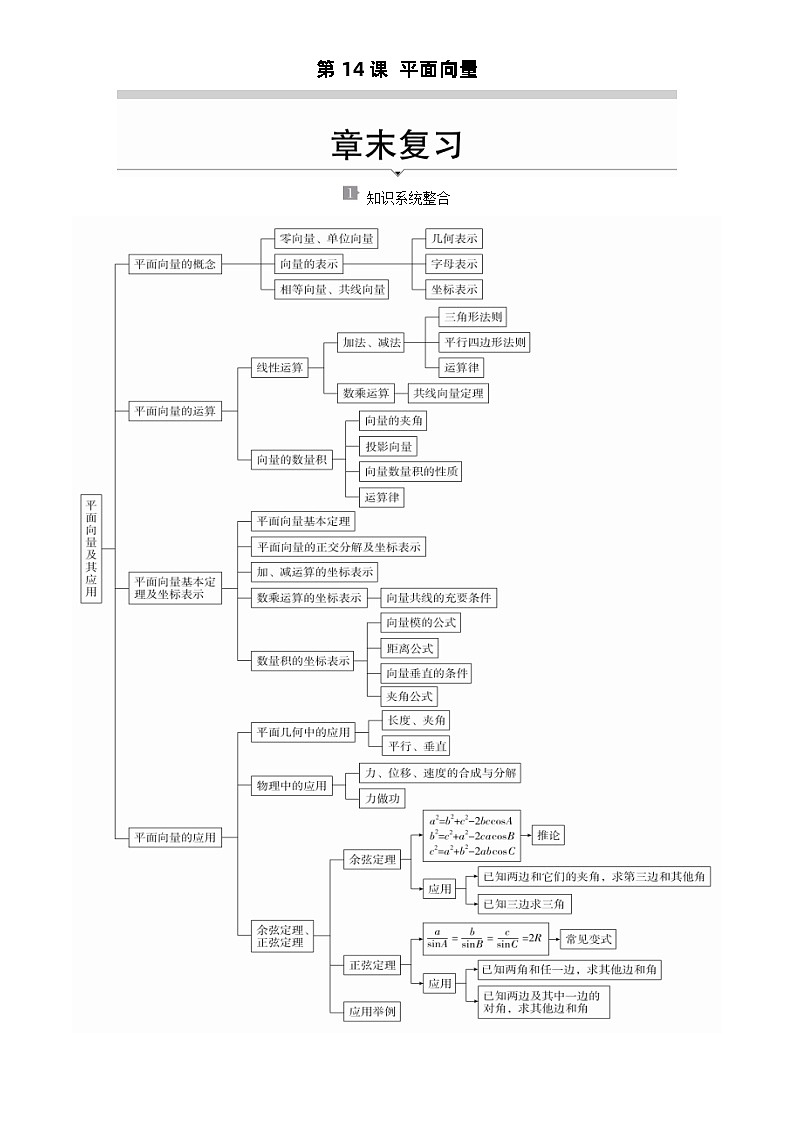
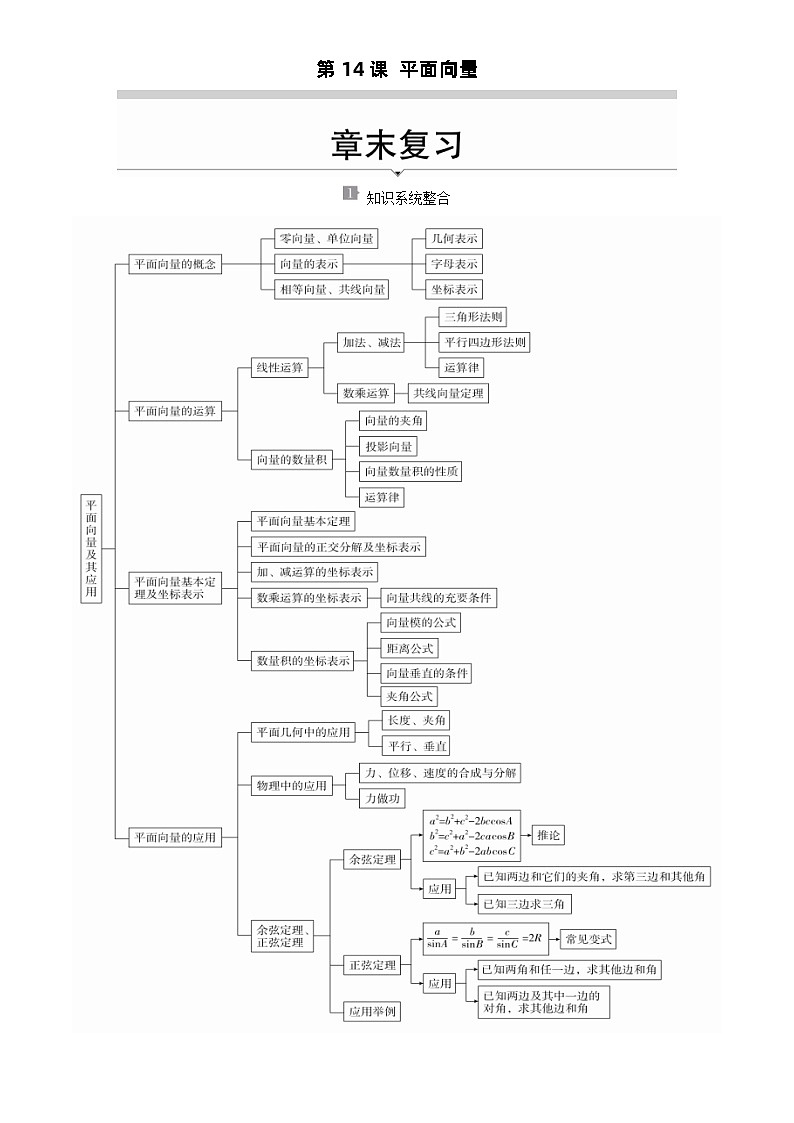
知识系统整合
规律方法
1.本章我们学习的向量具有大小和方向两个要素.用有向线段表示向量时，与有向线段的起点位置没有关系，同向且等长的有向线段都表示同一向量.数学中的向量指的是自由向量，根据需要可以进行平移.
2.共线向量条件和平面向量基本定理，揭示了共线向量和平面向量的基本结构，它们是进一步研究向量正交分解和用坐标表示向量的基础.
3.向量的数量积是一个数，当两个向量的夹角是锐角或零角时，它们的数量积为正数；当两个向量的夹角为钝角或180°角时，它们的数量积为负数；当两个向量的夹角是90°时，它们的数量积等于0.零向量与任何向量的数量积等于0.
通过向量的数量积，可以计算向量的长度(模)、平面内两点间的距离、两个向量的夹角，判断相应的两条直线是否垂直.
4.平面向量的应用中，用平面向量解决平面几何问题，要注意“三部曲”；用向量解决物理问题，体现了数学建模的要求，要根据题意结合物理意义作出图形，转化为数学问题，再通过向量运算使问题解决.
5.正、余弦定理将三角形边和角的关系进行量化，为我们解三角形或求三角形的面积提供了依据，而三角形中的问题常与向量、函数、方程及平面几何相结合，通常可以利用正、余弦定理完成证明，求值问题.
(1)解三角形与向量的交汇问题，可以结合向量的平行、垂直、夹角、模等知识转化求解.
(2)解三角形与其他知识交汇问题，可以运用三角形的基础知识，正、余弦定理、三角形的面积公式与三角恒等变换，通过等价转化构造方程及函数求解.
6.学习本章要注意类比，如向量的运算法则及运算律可与实数相应的运算法则及运算律进行横向类比.
7.向量是数形结合的载体.在本章学习中，一方面通过数形结合来研究向量的概念和运算；另一方面，我们又以向量为工具，运用数形结合的思想解决数学问题和物理的相关问题.同时，向量的坐标表示为我们用代数方法研究几何问题提供了可能，丰富了我们研究问题的范围和手段.
思想培优
向量的线性运算
向量的线性运算包含向量及其坐标运算的加法、减法、数乘，向量的加法遵循三角形法则和平行四边形法则，减法可以转化为加法进行运算，向量的加法满足交换律、结合律，数乘向量满足分配律，向量的线性运算也叫向量的初等运算，它们的运算法则在形式上很像实数加减法与乘法满足的运算法则，但在具体含义上是不同的.不过由于它们在形式上相类似，因此，实数运算中的去括号、移项、合并同类项等变形手段在向量的线性运算中都可以使用.如果e1，e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1，λ2，使a＝λ1e1＋λ2e2.
[典例1] 已知线段AB的端点为A(x,5)，B(﹣2，y)，直线AB上的点C(1,1)，且|Aeq \(C,\s\up6(→))|＝2|Beq \(C,\s\up6(→))|，求x，y的值.
向量的数量积运算
向量的数量积运算是本章的核心，由于向量数量积的运算及其性质涵盖向量的长度、角度以及不等式等，因此它的应用也最为广泛.利用向量的数量积可以求长度、也可判断直线与直线之间的关系(相交的夹角以及垂直)，还可以通过向量的坐标运算将代数中的有关函数、不等式等知识融合在一起.
[典例2] 平面内有向量eq \(OA,\s\up6(→))＝(1,7)，eq \(OB,\s\up6(→))＝(5,1)，eq \(OP,\s\up6(→))＝(2,1)，点M为直线OP上的一动点.
(1)当eq \(MA,\s\up6(→))·eq \(MB,\s\up6(→))取最小值时，求eq \(OM,\s\up6(→))的坐标；
(2)在(1)的条件下，求cs∠AMB的值.
向量的应用
向量的应用是多方面的，但由于我们所学的知识范围较窄，因此我们目前的应用主要限于平面几何以及用来探讨函数、三角函数的性质等方面，当然还有在物理方面的应用.
[典例3] 在△ABC中，eq \(AB,\s\up6(→))·eq \(AC,\s\up6(→))＝0，|eq \(AB,\s\up6(→))|＝12，|eq \(BC,\s\up6(→))|＝15，l为线段BC的垂直平分线，l与BC交于点D，E为l上异于D的任意一点.
(1)求eq \(AD,\s\up6(→))·eq \(CB,\s\up6(→))的值；
(2)判断eq \(AE,\s\up6(→))·eq \(CB,\s\up6(→))的值是否为一个常数，并说明理由.
[典例4]平面向量a＝(eq \r(3)，﹣1)，b＝(eq \f(1,2)，eq \f(\r(3),2))，若存在不同时为0的实数k和t，使x＝a＋(t2﹣3)b，y＝﹣ka＋tb，且x⊥y，试求函数关系式k＝f(t).
[典例5] 已知△ABC中，A(2,4)，B(﹣1，﹣2)，C(4,3)，BC边上的高为AD.
(1)求证：AB⊥AC；
(2)求点D和向量eq \(AD,\s\up6(→))的坐标；
(3)设∠ABC＝θ，求csθ；
(4)求证：AD2＝BD·CD.
[典例6] 在△ABC中，角A，B，C的对边分别为a，b，c，已知向量m＝(a＋c，b)与向量n＝(a﹣c，b﹣a)互相垂直.
(1)求角C；
(2)求sinA＋sinB的取值范围.
数形结合思想
向量本身既有大小，又有方向，可以用几何法表示，而向量又有良好的运算性质——坐标运算，可把向量与数联系起来，这样向量具备了“数”与“形”的两方面特征.两条直线平行、垂直，三点共线等几何问题，可通过向量的坐标运算这种代数手段实现证明，还可利用向量的数量积处理线段的长度、角度等问题.
[典例7] 已知向量a与b不共线，且|a|＝|b|≠0，则下列结论正确的是( )
A.向量a＋b与a﹣b垂直 B.向量a﹣b与a垂直
C.向量a＋b与a垂直 D.向量a＋b与a﹣b共线
[典例8] 已知向量eq \(OB,\s\up6(→))＝(2,0)，向量eq \(OC,\s\up6(→))＝(2,2)，向量eq \(CA,\s\up6(→))＝(eq \r(2)csα，eq \r(2)sinα)，则向量eq \(OA,\s\up6(→))与向量eq \(OB,\s\up6(→))的夹角的取值范围为( )
A.[0，eq \f(π,4)] B.[eq \f(π,4)，eq \f(5π,12)] C.[eq \f(5π,12)，eq \f(π,2)] D.[eq \f(π,12)，eq \f(5π,12)]
[典例9] 如图，A，B是海面上位于东西方向相距5(3＋eq \r(3))海里的两个观测点.现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20eq \r(3)海里的C点的救援船立即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？
单元巩固练习卷
一、单选题
1.下列各组平面向量中，可以作为基底的是（ ）
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A. SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三点共线 B. SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三点共线
C. SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三点共线 D. SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三点共线
3.如果向量 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，那么 SKIPIF 1 < 0 ( )
A.6 B.5 C.4 D.3
4.设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是两个不共线的平面向量，已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A.2 B.-2 C.6 D.-6
5.在 SKIPIF 1 < 0 中，下列各式正确的是（ ）
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
6.在矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在对角线 SKIPIF 1 < 0 上，点 SKIPIF 1 < 0 在边 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A. SKIPIF 1 < 0 B.4 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
7.已知 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的一个内角，向量 SKIPIF 1 < 0 .若 SKIPIF 1 < 0 ，则角 SKIPIF 1 < 0 ( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
8.海伦公式是利用三角形的三条边的边长 SKIPIF 1 < 0 直接求三角形面积S的公式，表达式为： SKIPIF 1 < 0 ；它的特点是形式漂亮，便于记忆.中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”，虽然它与海伦公式形式上有所不同，但它与海伦公式完全等价，因此海伦公式又译作海伦－秦九韶公式.现在有周长为 SKIPIF 1 < 0 的 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则用以上给出的公式求得 SKIPIF 1 < 0 的面积为（ ）
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D.12
二、多选题
9.已知两点 SKIPIF 1 < 0 ，与 SKIPIF 1 < 0 平行，且方向相反的向量 SKIPIF 1 < 0 可能是（ ）
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
10.已知向量 SKIPIF 1 < 0 (2，1)， SKIPIF 1 < 0 (1，﹣1)， SKIPIF 1 < 0 (m﹣2，﹣n)，其中m，n均为正数，且( SKIPIF 1 < 0 )∥ SKIPIF 1 < 0 ，下列说法正确的是（ ）
A.a与b的夹角为钝角 B.向量a在b方向上的投影为 SKIPIF 1 < 0
C.2m＋n＝4 D.mn的最大值为2
11.对于三角形ABC，有如下判断，其中正确的判断是（ ）
A.若sin2A＋sin2B＜sin2C，则三角形ABC是钝角三角形
B.若A＞B，则sin A＞sin B
C.若a＝8，c＝10，B＝60°，则符合条件的三角形ABC有两个
D.若三角形ABC为斜三角形，则 SKIPIF 1 < 0
12.在 SKIPIF 1 < 0 中，a，b，c分别为角A，B，C的对边，已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则（ ）
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
三、填空题
13.已知向量 SKIPIF 1 < 0 .若 SKIPIF 1 < 0 与 SKIPIF 1 < 0 共线，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 方向上的投影为 ________.
14.已知平面向量 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的夹角为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为________.
15.在山顶铁塔上 SKIPIF 1 < 0 处测得地面上一点 SKIPIF 1 < 0 的俯角 SKIPIF 1 < 0 ，在塔底 SKIPIF 1 < 0 处测得点 SKIPIF 1 < 0 的俯角 SKIPIF 1 < 0 ，已知铁塔 SKIPIF 1 < 0 部分高 SKIPIF 1 < 0 米，山高 SKIPIF 1 < 0 _______.
16.在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，点M为 SKIPIF 1 < 0 三边上的动点，PQ是 SKIPIF 1 < 0 外接圆的直径，则 SKIPIF 1 < 0 的取值范围是_______________________
四、解答题
17.已知向量 SKIPIF 1 < 0 （csx， SKIPIF 1 < 0 csx）， SKIPIF 1 < 0 （csx，sinx）.
（1）若 SKIPIF 1 < 0 ∥ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求x的值；
（2）若f（x） SKIPIF 1 < 0 • SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求f（x）的最大值及相应x的值.
18.已知 SKIPIF 1 < 0 是平面内两个不共线的非零向量， SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 ，且A，E，C三点共线.
（1）求实数λ的值；
（2）若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的坐标；
（3）已知 SKIPIF 1 < 0 ，在（2）的条件下，若 SKIPIF 1 < 0 四点按逆时针顺序构成平行四边形，求点A的坐标.
19. SKIPIF 1 < 0 的角A，B，C的对边分别为a，b，c，已知 SKIPIF 1 < 0 .
（1）求角A；
（2）从三个条件：① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 中任选一个作为已知条件，求 SKIPIF 1 < 0 周长的取值范围.
20.在 SKIPIF 1 < 0 中，角 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的对边分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，已知 SKIPIF 1 < 0 .
（1）若 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值；
（2）设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值.
21.如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
（1）求 SKIPIF 1 < 0 的长；
（2）求 SKIPIF 1 < 0 的值.
22.在 SKIPIF 1 < 0 中，内角 SKIPIF 1 < 0 的对边分别为 SKIPIF 1 < 0 ，设平面向量 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0
（Ⅰ）求 SKIPIF 1 < 0 ；
（Ⅱ）若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 中边上的高 SKIPIF 1 < 0 .