



- 专题10 随机事件与求概率之六大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题11 反比例函数的图象和性质之八大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题12 反比例函数与几何图形、实际应用的综合问题之五大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编(人教版) 试卷 1 次下载
- 专题13 图形相似、相似三角形与位似作图及性质之十大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
- 专题14 锐角三角形函数及应用之六大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编(人教版) 试卷 0 次下载
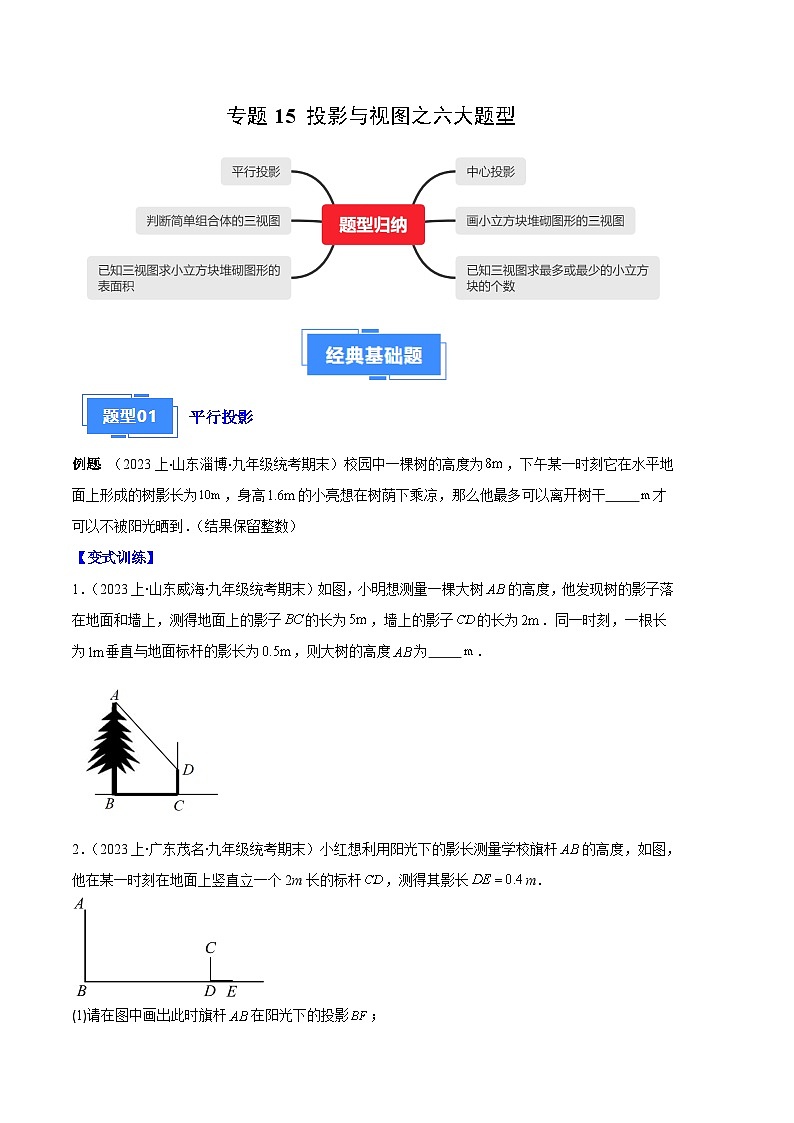
专题15 投影与视图之六大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编(人教版)
展开平行投影
例题:(2023上·山东淄博·九年级统考期末)校园中一棵树的高度为,下午某一时刻它在水平地面上形成的树影长为,身高的小亮想在树荫下乘凉,那么他最多可以离开树干 才可以不被阳光晒到.(结果保留整数)
【答案】8
【分析】在同一时刻时,树的高度与影长与人的高度与影长成正比列比例式,求出此时人的影长,计算出最多离树干的长度.
【详解】解:设小亮在这个时刻水平地面上形成的影长为,根据题意得:
,
解得:,
即小亮在这个时刻水平地面上形成的影长为,
,
∴他最多可以离开树干才可以不被阳光晒到.
故答案为:8
【点睛】本题考查了平行投影,一个不透明的物体由平行光线形成的投影是平行投影,在平行投影中,同一时刻,物高和影长成正比.
【变式训练】
1.(2023上·山东威海·九年级统考期末)如图,小明想测量一棵大树的高度,他发现树的影子落在地面和墙上,测得地面上的影子的长为,墙上的影子的长为.同一时刻,一根长为垂直与地面标杆的影长为,则大树的高度为 .
【答案】12
【分析】设地面影长对应的树高为,根据同时同地物高与影长成正比列出比例式求出,然后加上墙上的影长即为树的高度.
【详解】解:设地面影长对应的树高为,
由题意得,,
解得,
墙上的影子长为,
树的高度为.
故答案为:12.
【点睛】本题考查利用投影求物高.熟练掌握同时同地物高与影长成正比是解题的关键.
2.(2023上·广东茂名·九年级统考期末)小红想利用阳光下的影长测量学校旗杆的高度,如图,他在某一时刻在地面上竖直立一个2m长的标杆,测得其影长m.
(1)请在图中画出此时旗杆在阳光下的投影;
(2)如果m,求旗杆的高.
【答案】(1)见解析
(2)旗杆的高为.
【分析】(1)根据太阳光是平行光,画出图即可;
(2)根据太阳光是平行光,可得,可证明,再根据对应边成比例即可得出答案.
【详解】(1)解:连接,过A点作交于,则为所求,如图;
(2)∵,
∴,
而,
∴,
∴,即,
∴m.
答:旗杆的高为m.
【点睛】本题考查投影作图,相似三角形的判断和性质,理解太阳光是平行光,并证明出三角形相似是解题的关键.
中心投影
例题:(2023上·四川雅安·九年级统考期末)如图,李强从距离路灯底部O为20米的点A处沿方向行走10米到达点C处,李强在A处时,他在路灯下的影子为线段.
(1)已知路灯杆垂直于路面,请在图中画出路灯P的位置和李强走到点C处时在路灯下的影子;
(2)若路灯的高度是8米,李强的身高是1.6米,求李强在点C处的影子的长度.
【答案】(1)见解析
(2)李强在点C处的影子的长度为 2.5米
【分析】(1)连接并延长,与过点O且垂直于路面的直线相交于点P,点P即为路灯的位置,连接并延长交路面于点N,即为李强走到点C处时在路灯下的影子;
(2)易得,利用相似三角形对应边成比例列式求出即可.
【详解】(1)解:如图,路灯P,影子即为所求;
(2)解:由题意得:,米,米,则米,
设米.
∵,
∴,
∴,即,
∴,
答:李强在点C处的影子的长度为2.5米.
【点睛】本题考查了中心投影以及相似三角形的应用,解题的关键是掌握如何确定点光源以及相似三角形的判定和性质.
【变式训练】
1.(2023上·江苏南京·九年级统考期末)如图,道路l的正上方挂有一盏路灯M,把路灯M看成一个点光源,路灯M到道路l的距离为,晚上,一名身高为的小女孩沿着道路l散步,从A处径直向前走到达C处.已知小女孩在A处影子的长为,在C处影子的长为,求小女孩的身高.
【答案】
【分析】根据相似三角形的判定和性质得出,,再由等量代换得出,求解确定,然后代入原式中求解即可.
【详解】解:根据题意得,
∴,
∴,,
∵,
∴,即,
∵,
∴,
代入求解得:,
∴,
∵,
∴,
解得:,
∴小女孩的身高为.
【点睛】题目主要考查相似三角形的判定和性质即应用举例,理解题意,熟练掌握相似三角形的判定和性质是解题关键.
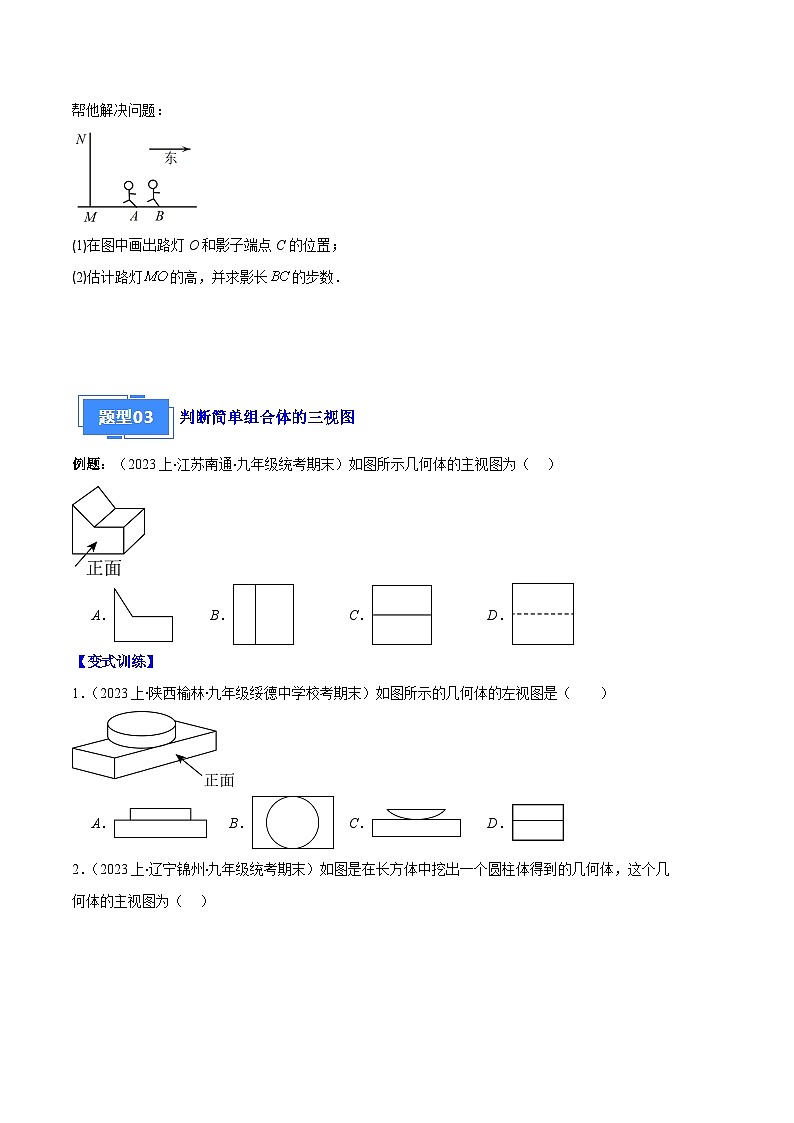
2.(2023上·江苏盐城·九年级统考期末)元宵节晚上,小王与爸爸妈妈看灯会,他想了解路边路灯的大致高度.具体做法如下:如图,先从路灯灯柱MN底部M向东走25步到A处,发现自己的影子端点落在B处,作标记后,继续沿刚才自己的影子走5步恰好到达点B处,此时影子的端点在C处,已知小王和灯柱的底端在同一水平线上,且小王每步的间距相同.若小王的身高是,请帮他解决问题:
(1)在图中画出路灯O和影子端点C的位置;
(2)估计路灯的高,并求影长的步数.
【答案】(1)见解析
(2),步
【分析】(1)根据中心投影的定义画出图形即可;
(2)由得,代入数值可求出,由得,代入数值可求出的长.
【详解】(1)如图所示,
(2)∵,
∴,
∴,
∴
∴.
∵,
∴
∴,
∴,
∴步.
【点睛】本题考查作图-应用与设计作图,中心投影,相似三角形的判定与性质的应用,解题的关键是掌握中心投影的性质.
判断简单组合体的三视图
例题:(2023上·江苏南通·九年级统考期末)如图所示几何体的主视图为( )
A. B. C. D.
【答案】A
【分析】根据三视图的特点,主视图是从正面看到立体图形的视角,即立体图形正面的线条组成的平面图形,即可求解.
【详解】解:、是主视图,符合题意;
、是俯视图,不符合题意;
、不是三视图,不符合题意;
、是左视图,不符合题意;
故选:.
【点睛】本题主要考查立体图形的三视图,掌握各视图的定义及特点是解题的关键.
【变式训练】
1.(2023上·陕西榆林·九年级绥德中学校考期末)如图所示的几何体的左视图是( )
A. B. C. D.
【答案】D
【分析】根据左视图就是从物体的左边进行观察,得出左视图即可.
【详解】解:在三视图中,此几何体从左边看是两个长方形,上面是一个小长方形,下面是个大长方形,
故选:D.
【点睛】本题主要考查了三视图的画法中左视图画法,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
2.(2023上·辽宁锦州·九年级统考期末)如图是在长方体中挖出一个圆柱体得到的几何体,这个几何体的主视图为( )
A. B. C. D.
【答案】A
【分析】根据从正面看可得主视图,看不见的用虚线表示解答即可;
【详解】从正面看是个长方形,看不到里面的圆柱,故是虚线
故选A.
【点睛】本题考查了三视图的知识,掌握主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图是解题的关键.
画小立方块堆砌图形的三视图
例题:(2023上·江苏南京·七年级统考期末)如图是一个由7个正方体组成的立体图形.画出该立体图形的主视图、左视图和俯视图.
【答案】见解析
【分析】根据三视图的意义,画出图形,即可求解.
【详解】解:如图:
【点睛】本题主要考查了几何体的三视图,熟练掌握三视图是观测者从三个不同位置观察同一个几何体,画出的平面图形;(1)主视图:从物体前面向后面正投影得到的投影图,它反映了空间几何体的高度和长度;(2)左视图:从物体左面向右面正投影得到的投影图,它反映了空间几何体的高度和宽度;(3)俯视图:从物体上面向下面正投影得到的投影图,它反应了空间几何体的长度和宽度是解题的关键.
【变式训练】
1.(2022上·河南洛阳·七年级统考阶段练习)如图是由8个相同的小正方体组成的几何体,请画出这一几何体的三视图.
【答案】见解析
【分析】根据主视图、左视图、俯视图的定义即可得到结果.
【详解】∵从正面看如下图所示:
∴三视图如下图所示:
【点睛】本题考查了画小立方块堆砌图形的三视图,熟练掌握三视图的画法是解题关键.
2.(2022上·陕西汉中·七年级统考期末)如图是由9个正方体堆成的几何体,画出这一几何体的三视图.
【答案】见解析
【分析】根据三视图的作法作图即可.
【详解】解:如图所示.
【点睛】本题考查三视图的作法,熟练掌握三视图的作法是解题的关键.
已知三视图求小立方块堆砌图形的表面积
例题:(2023上·河南南阳·七年级统考期末)如图是由若干个边长为1的立方体搭成的几何体从上面看到的平面图形,小正方形中的数字表示该位置立方体的个数.
(1)请画出该几何体正视图和左视图.
(2)该几何体的表面积为______.
【答案】(1)见解析
(2)26
【分析】(1)根据俯视图知,分两排,前排左边上下3个;后排左边一个,右边上下两个,由此可画出正视图与左视图;
(2)直接计算即可.
【详解】(1)解:所画的正视图与左视图如下:
(2)解:
故答案为:26.
【点睛】本题考查了三视图,根据俯视图画出正视图与三视图,计算表面积,具备一定的空间想象力是解题的基础.
【变式训练】
1.(2023上·辽宁阜新·七年级阜新实验中学校考期末)在水平的桌面上,由若干个完全相同棱长为的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图、左视图和俯视图;
(2)若给该几何体露在外面的喷上红漆(不含几何体的底面),则需要喷漆的面积是______?
【答案】(1)见解析
(2)3200
【分析】(1)根据物体形状即可画出主视图、左视图和俯视图;
(2)利用几何体的形状求出其表面积即可,注意不含底面.
【详解】(1)解:这个几何体的主视图、左视图和俯视图,如图:
(2)解∶
答:需要喷漆的面积是.
【点睛】本题考查了三视图的画法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意看到的用实线表示,看不到的用虚线表示.注意涂色面积指组成几何体的外表面积.
已知三视图求最多或最少的小立方块的个数
例题:(2023上·河南新乡·七年级统考期末)按要求画图并解答:
(1)如图几何体由大小相同的7块小立方体搭成,请在如图的方格中画出该几何体的三视图.
(2)如果在这个几何体上再添加一些相同的小立方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加__________个小正方体.
【答案】(1)见解析
(2)2
【分析】(1)根据简单组合体的三视图的画法,画出几何体的三视图即可;
(2)保持俯视图和主视图不变,可往第一列前面的第二个小正方形上添加2个小正方体,即可求解.
【详解】(1)解:如图所示,
(2)保持俯视图和主视图不变,可往第一列前面的第二个小正方形上添加2个小正方体,
故答案为2.
【点睛】此题主要考查了三视图,正确掌握不同视图的观察角度是解题关键.
【变式训练】
1.(2023上·江苏宿迁·七年级统考期末)如图是由一些棱长都为1的小正方体组合成的简单几何体.
(1)画出该几何体的主视图、左视图和俯视图;
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加 块小正方体.
【答案】(1)见解析
(2)3
【分析】(1)根据三视图的定义画出图形即可.
(2)根据题目条件解决问题即可.
【详解】(1)如图所示:
(2)在这个几何体上再添加一些小正方体,并保持俯视图和左视图不变,可以在中间列上添加一个,最右边一列上加两个,最多可以再添加3个小正方体,
故答案为:3.
【点睛】此题主要考查了画三视图,关键是在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
2.(2022上·四川成都·七年级校考期中)如图,在平整的地面上,用10个棱长都为的小正方体堆成一个几何体.
(1)画出这个几何体的三视图;
(2)求这个几何体的表面积;
(3)如果现在你还有一些棱长都为的小正方体,要求保持俯视图和左视图都不变,最多可以再添加 个小正方体.
【答案】(1)见解析
(2)
(3)5
【分析】(1)根据三视图的定义画出图形即可;
(2)判断出表面正方形的个数,可得结论;
(3)利用俯视图,左视图解决问题即可.
【详解】(1)解:三视图如图所示:
(2)解:这个几何体的表面积为:;
(3)解:要求保持俯视图和左视图都不变,最多可以再添加(个)正方形.
故答案为:5.
【点睛】本题主要考查作图-三视图,几何体的表面积等知识,解题的关键是理解三视图的定义,属于中考常考题型.
一、单选题
1.(2022上·河南平顶山·九年级统考期末)在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A. B. C. D.
【答案】D
【分析】平行投影特点:在同一时刻,不同物体的影子同向,且不同物体的物高和影长成比例.
【详解】解:A.影子的方向不相同,故本选项错误;
B. 影子的方向不相同,故本选项错误;
C.相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,故本选项错误;
D. 影子平行,且较高的树的影子长度大于较低的树的影子,故本选项正确;
故选:D.
【点睛】本题考查了平行投影特点,难度不大,注意结合选项判断.
2.(2023上·山西太原·九年级期末)如图是一个空心圆柱,关于它的主视图和俯视图正确的是( )
A.B.C.D.
【答案】B
【分析】根据从正面看和从上面看得到的图形,进行判断即可.
【详解】解:该几何体的主视图和俯视图为:
故选B.
【点睛】本题考查三视图.熟练掌握三视图的画法,是解题的关键.注意存在看不见的用虚线表示.
3.(2023上·山西晋中·九年级统考期末)如图,三角板在手电筒光源的照射下形成了投影,三角板与其投影是位似图形,其相似比是,若三角板的面积是,则其投影的面积是( )
A.B.C.D.
【答案】D
【分析】利用位似图形的面积比等于相似比的平方进行计算即可;
【详解】解:设投影的面积为cm,,cm,
故选:D.
【点睛】本题考查位似图形的面积关系,解题关键掌握位似图形的面积比等于相似比的平方.
4.(2023上·山东淄博·九年级统考期末)如图,是由一些大小相同的小正方体搭成的几何体的主视图和左视图,则搭成该几何体的小正方体的个数最少是( )
A.3B.4C.5D.6
【答案】C
【分析】做出相应的俯视图,标出搭成该几何体的小正方体的个数最少时的数字即可.
【详解】由题中所给出的主视图知小正方体共两列,且左侧一列有一层,右侧一列有两层;
由左视图可知小正方体共两列,左,右都是两层.各层最最少如俯视图,
或
所以图中的小正方体最少5个小正方体.
故选:C.
【点睛】本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
5.(2023上·河北保定·九年级统考期末)某学习小组测量旗杆高度,并做出示意图:为旗杆,为旗杆的影子,为一位小组成员,为该成员的影子,在同一时刻测得米,米,米,则旗杆的高度为( )
A.9米B.12米C.15米D.18米
【答案】B
【分析】由太阳光为平行光可知,进而证明,利用相似三角形对应边成比例,即可列式求解.
【详解】解:由题意知,
,
又,
,
,即,
,
即旗杆的高度为12米.
故选B.
【点睛】本题主要考查相似三角形的判定与性质、平行投影、平行线的性质,解题的关键是掌握相似三角形的判定方法.
二、填空题
6.(2023上·江苏盐城·七年级统考期末)一个长方体的主视图和左视图如图所示(单位:),其体积是 .
【答案】
【分析】主视图是一个长,高的长方形,左视图是一个宽,高的长方形,可知是一个长方体,根据长方体的体积计算公式即可求解.
【详解】解:根据题意可知,长方体的长,宽,高的长方形,
∴体积为,
故答案为:.
【点睛】本题主要考查几何体的三视图,体积的计算,理解三视图的特点,体积的计算公式是解题的关键.
7.(2023上·山西晋中·九年级统考期末)宋代诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”手影戏是一种独特的艺术形式,它的表演全部靠手部动作投影的改变,幻化形成各种不同的形象.“手影戏”中的手影属于 .(填写“平行投影”或“中心投影”)
【答案】中心投影
【分析】根据中心投影和平行投影的定义即可判断.
【详解】解:由图可知,“手影戏”中的投影是光由一点向外散射形成的投影,属于中心投影,
故答案为:中心投影.
【点睛】本题考查中心投影和平行投影的识别,解题的关键是掌握两者的定义:中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影.
8.(2023上·陕西咸阳·九年级统考期末)如图,小树在路灯O的照射下形成树影.若树高,树影,树与路灯的水平距离,点P、B、C在同一直线上,,,则路灯的高度OP为 .
【答案】/
【分析】利用相似三角形的性质求解即可.
【详解】解:由题意得,
∴,
∴,即,
∴,
故答案为:.
【点睛】本题考查中心投影,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识.
9.(2023上·山东泰安·九年级校考期末)如图,是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是 个.
【答案】4
【分析】根据俯视图可知底层个数,由主视图、左视图可知上层正方体的个数及位置即可得答案.
【详解】解:由俯视图可知,这个几何体的底层有3个小正方体,
结合主视图、左视图可知上层后排右侧有1个正方体,
所以组成该几何体的小正方体的个数是4个,
故答案为:4.
【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
10.(2023上·湖南邵阳·九年级统考期末)如图,小明晚上由路A下的B处走到C处时,测得影子的长为1米,继续往前走3米到达E处时,测得影子的长为2米,已知小明的身高是米,那么路灯的高度等于 米.
【答案】
【分析】根据题意可知:,当小明在处时,,即,当小明在处时,,即,由,可得,设,,可得,可得,再根据,可得:,问题随之得解.
【详解】解:如图,根据题意可知:,
∵,
当小明在处时,,
即,
当小明在处时,,
即,
∵身高不变,即,
∴,即,
∵米,米,米,米,
设,,
∴,即,即,
解得:(经检验,此根是原方程的解),
即根据,可得:,
解得,,(经检验,此根是原方程的解),
即路灯A的高度米.
故答案为:.
【点睛】本题综合考查了中心投影的特点和规律以及相似三角形性质的运用.解题的关键是利用中心投影的特点可知在这两组相似三角形中有一组公共边,利用其作为相等关系求出所需要的线段,再求公共边的长度.
三、作图题
11.(2022上·陕西汉中·七年级统考期末)如图是由一些棱长为1的相同的小正方体组合成的简单几何体.
(1)请在相应方格纸中分别画出该几何体的视图;
(2)这个几何体的表面积是_________.
【答案】(1)见解析
(2)38
【分析】(1)根据简单组合体的三视图的画法,画出从正面、上面、左面看该组合体所看到的图形即可;
(2)根据表面积的计算方法求解即可.
【详解】(1)如图所示:
;
(2).
故答案为:38.
【点睛】此题考查了三视图,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.
12.(2022上·江苏盐城·七年级统考期末)在平整的地面上,有若干个完全相同的棱长为1的小正方体堆成的一个几何体,如图所示.
(1)请画出这个几何体的三视图.
(2)若现在你手头还有一些相同的小正方体,如果保持主视图和左视图不变,最多可以再添加_____个小正方体.
(3)如果需要给原来这个几何体表面喷上蓝漆(接触地面部分不喷漆),则喷漆面积是多少?
【答案】(1)见解析
(2)6
(3)29cm2
【分析】(1)根据三视图的画法,画出从正面、左面、上面看到的形状即可;
(2)主视图和左视图不变,构成图形即可解决问题;
(3)求出这个几何体的表面积即可解决问题.
【详解】(1)这个几何体有8个立方体构成,三视图如图所示;
(2)最多可以加六个小正方体,具体放的方式,通过俯视图来展示,如下图:
故答案为:6;
(3)根据8个小正方体摆放的位置可以发现,从左看与从右看看到的面一样多为6个,从前看和从后看看到的面也一样多为6个,俯视图看到的面是5个,
∴需要喷漆的面的个数为:,
故喷漆面积为29.
【点睛】本题考查了三视图的画法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意看到的用实线表示,看不到的用虚线表示.注意涂色面积指组成几何体的外表面积.
13.(2023上·山东淄博·九年级统考期末)顾老师布置了周末实践性作业如下,利用影子测量路灯灯泡的高.
身高为米的小明为了完成老师布置的作业,他设计了如下方案,如图所示,他先从路灯底部(A处)向东走20步到B处,发现自己的影子端点在C处,继续沿刚才自己的影子走5步到C处,此时影子的端点在D处(假设公路是东西方向笔直的公路).根据小明设计的方案,请解决下列问题:
(1)请在图中画出路灯,
(2)估计路灯灯泡的高度并求影长.
【答案】(1)见解析
(2)路灯高8米,影长为步
【分析】(1)分别连接并延长,相交于点E,过点E作于点A,即为所求;
(2)根据可得,则,即可求出,根据,即可求出.
【详解】(1)解:如图所示:
(2)根据题意可得:步,步,,
∵,
∴,
∴,
∴,即,
解得:,
,即,
解得:,
综上:路灯高8米,影长为步.
【点睛】本题主要考查了中心投影,相似三角形的判定和性质,解题的关键是熟练掌握中心投影的性质和确定点光源的方法,以及相似三角形对应边成比例的性质.
14.(2023上·陕西汉中·九年级统考期末)如图,为一盏路灯的灯杆,已知该路灯的灯泡P位于灯杆上,地面上竖立着一个矩形单杠,已知单杠右侧杆在路灯灯泡P的照射下的影子末端位于点E处,已知O、B、C、E在一条直线上,且,,.
(1)请在图中找出路灯灯泡P的位置,并画出单杠左侧杆在灯泡P的照射下的影子;
(2)经测量米,米,单杠的高度米,请你计算路灯灯泡距地面的高度.
【答案】(1)见解析
(2)米
【分析】(1)连接并延长交于点P,连接并延长交于F,点P和即为所求;
(2)先求出米,证明,得到,即,则米.
【详解】(1)解:如图所示,点P和即为所求;
(2)解:∵米,米,
∴米,
∵,,即,
∴,
∴,即,
∴米,
∴路灯灯泡距地面的高度为米.
【点睛】本题主要考查了相似三角形的应用举例,熟知相似三角形的性质与判定条件是解题的关键.
15.(2023上·河北邯郸·九年级校考期末)某数学兴趣小组的名同学利用课余时间想要测量学校里两棵树的高度,在同一时刻的阳光下,他们合作完成了以下工作:
(1)测得一根长为米的竹竿的影长为米,甲树的影长为米(如图1).
(2)测量的乙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图2),测得落在地面上的影长为米,一级台阶高为米,落在第一级台阶的影子长为米,
①甲树的高度为______米,
②图3为图2的示意图,请利用图3求出乙树的高度.
【答案】(1)
(2)米
【分析】(1)根据同一时间竹竿的高度与影长之比等于树的长度与树的影长之比即可求得;
(2)根据相似三角形的判定和性质即可得出结论.
【详解】(1)解:设甲树的高度为米
根据题意得:
解得:
故答案为:
(2)解:连接并延长交的延长线于,延长交于,连接,
∵米,米,米
∴(米)
∴
∴
∴(米)
∴(米)
答:乙树的高度为米.
【点睛】本题考查了相似三角形的应用,根据相似三角形列出比例式是解题的关键.
16.(2023上·山西太原·九年级山西大附中校考期末)小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将木杆水平放置,此时木杆在水平地面上的影子为线段.
①若木杆的长为,则其影子的长为___________;
②在同一时刻同一地点,将另一根木杆直立于地面,请画出表示此时木杆在地面上影子的线段:
(2)如图2,夜晚在路灯下,小桃将木杆水平放置,此时木杆在水平地面上的影子为线段.
①请在图中画出表示路灯灯泡位置的点;
②若木杆的长为,经测量木杆距离地面,其影子的长为,则路灯距离地面的高度为___________.
【答案】(1)①;②见解析;
(2)①见解析;②
【分析】(1)①根据题意证得四边形为平行四边形,从而求得结论;
②根据平行投影的特点作图:过木杆的顶点作太阳光线的平行线;
(2)①分别过影子的端点及其线段的相应的端点作射线,两条射线的交点即为光源的位置;
②根据,可证得,利用相似三角形对应高的比等于相似比即可求得结论.
【详解】(1)①根据题意:,,
∴四边形为平行四边形,
∴;
②如图所示,线段即为所求;
(2)①如图所示,点即为所求;
②过点作分别交、于点、
∵
∴
,,
解得:,
路灯距离地面的高度为米.
【点睛】本题考查平行投影问题以及相似三角形的判定和性质,平行光线得到的影子是平行光线经过物体的顶端得到的影子,利用相似三角形对应高的比等于相似比是解决本题的关键.
专题12 分式与分式方程中常见的易错之六大题型-【备考期末】2023-2024学年八年级数学上学期期末真题分类汇编(人教版): 这是一份专题12 分式与分式方程中常见的易错之六大题型-【备考期末】2023-2024学年八年级数学上学期期末真题分类汇编(人教版),文件包含专题12分式与分式方程中常见的易错之六大题型原卷版docx、专题12分式与分式方程中常见的易错之六大题型解析版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
专题08 平方差公式与完全平方公式之六大题型-【备考期末】2023-2024学年八年级数学上学期期末真题分类汇编(人教版): 这是一份专题08 平方差公式与完全平方公式之六大题型-【备考期末】2023-2024学年八年级数学上学期期末真题分类汇编(人教版),文件包含专题08平方差公式与完全平方公式之六大题型原卷版docx、专题08平方差公式与完全平方公式之六大题型解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
专题11 线段上的动点与几何图形动角的探究问题之六大题型-【备考期末】2023-2024学年七年级数学上学期期末真题分类汇编(人教版): 这是一份专题11 线段上的动点与几何图形动角的探究问题之六大题型-【备考期末】2023-2024学年七年级数学上学期期末真题分类汇编(人教版),文件包含专题11线段上的动点与几何图形动角的探究问题之六大题型原卷版docx、专题11线段上的动点与几何图形动角的探究问题之六大题型解析版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。












