苏科版九年级下册7.5 解直角三角形同步训练题

这是一份苏科版九年级下册7.5 解直角三角形同步训练题，文件包含苏教版九年级数学下册同步精品讲义第17讲解直角三角形教师版docx、苏教版九年级数学下册同步精品讲义第17讲解直角三角形学生版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。

目标导航
知识精讲
知识点01 解直角三角形
在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.
在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.
设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：
①三边之间的关系：a2+b2=c2(勾股定理).
②锐角之间的关系：∠A+∠B=90°.
③边角之间的关系：
，，，
，，.
④，h为斜边上的高.
【微点拨】
(1)直角三角形中有一个元素为定值(直角为90°)，是已知值.
(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系。
(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解。
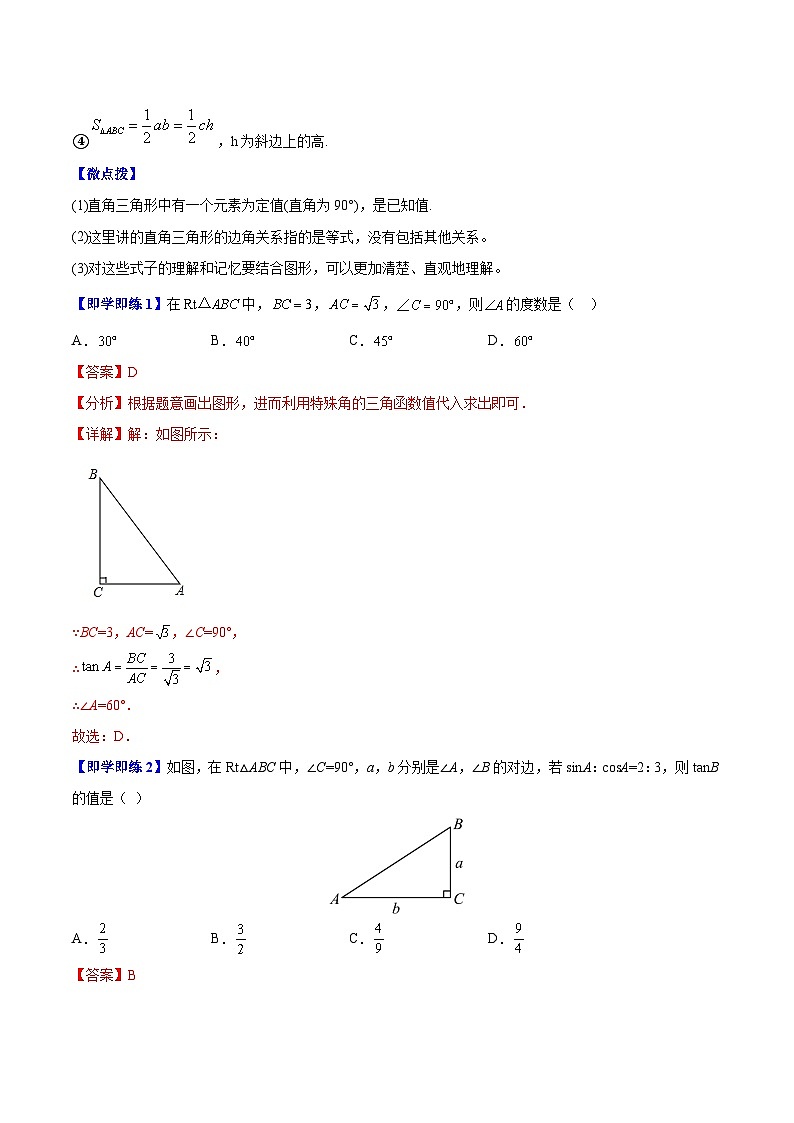
【即学即练1】在中，，，，则的度数是（ ）
A．B．C．D．
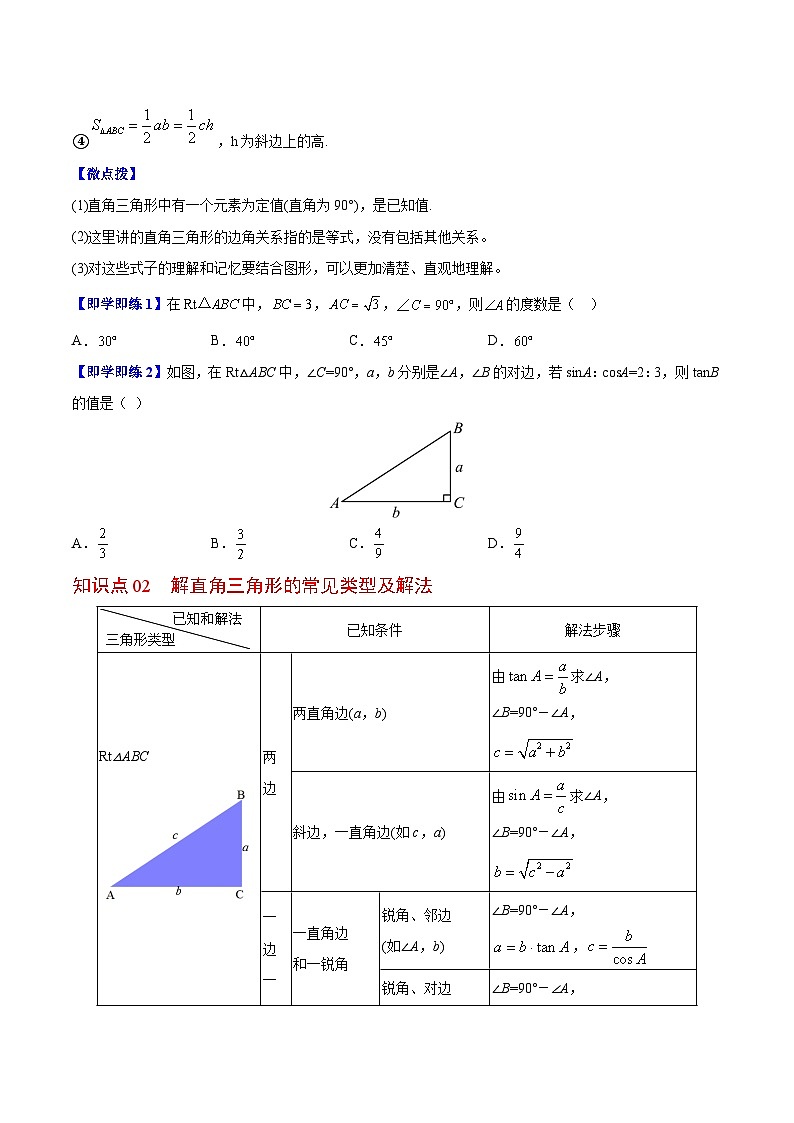
【即学即练2】如图，在Rt△ABC中，∠C=90°，a，b分别是∠A，∠B的对边，若sinA：csA=2：3，则tanB的值是（ ）
A．B．C．D．
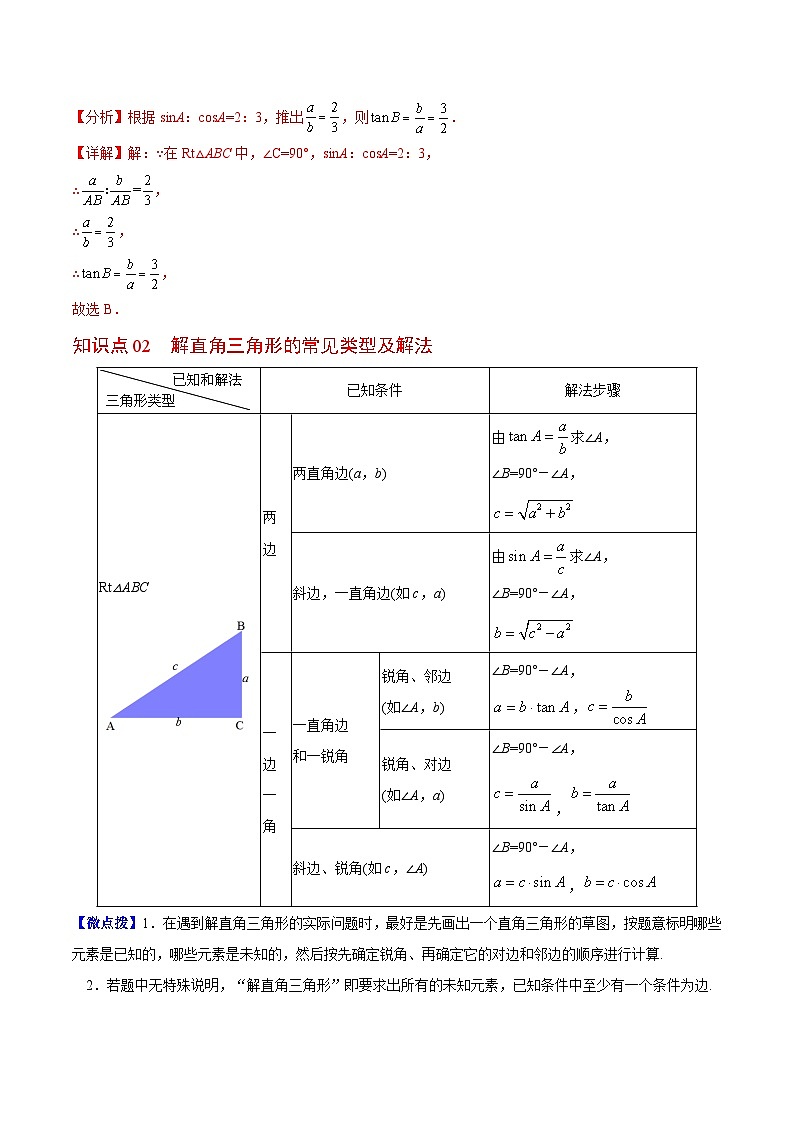
知识点02 解直角三角形的常见类型及解法
【微点拨】1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.
2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.
【即学即练3】在△ABC中，AB：AC：BC＝1：2：，则tanB的值为（ ）
A．2B．1C．D．
能力拓展
考法 解直角三角形
【典例】如图，在中，，，，，，分别在，，上，则周长的最小值是（ ）
A．B．C．D．
分层提分
题组A 基础过关练
1．如图，在平面直角坐标系中，点A的坐标为(﹣1，2)，以点O为圆心，将线段OA逆时针旋转，使点A落在x轴的负半轴上点B处，则点B的横坐标为（ ）
A．﹣B．C．﹣D．
2．如图，点C在以AB为直径的圆上，则BC＝（ ）
A．B．C．D．
3．如图，在Rt△ABC中，，，，将△ABC绕点A逆时针旋转得到，使点落在AB边上，连结，则的值为（ ）
A．B．C．D．
4．在 Rt△ABC 中， C  90 ， AB  5 ， AC  4 ．下列四个选项，正确的是（ ）
A．tan B B．ct B C．sin B D．cs B 
5．在△ABC中，AB=4，BC=5，sinB =，则△ABC的面积等于（ ）
A．15B．C．6D．
6．如图，在中，，点D为AB边的中点，连接CD，若，，则的值为（ ）
A．B．C．D．
7．Rt△ABC中，，，AB=，则AC= ____________ ．
8．公园有一个亭子的底面是边长为2m的正六边形，这个正六边形底面的面积是____m2．
9．如图， ，点P在OA上， PC=PD，若CO=5cm，OD=8cm ，则 OP的长是___________．
10．如图所示，四边形ABCD中，∠B＝90°，AB＝2，CD＝8，AC⊥CD，若sin∠ACB＝，则cs∠ADC＝______．
题组B 能力提升练
1．如图，PA，PB是⊙O的两条切线，切点分别为A，B．连接OA、OB、AB、PO，PO与AB交于点C．若，OC=1，则PO的长为（ ）
A．12B．8C．D．4
2．在Rt△ABC中，∠C=90°，AB=5，AC=4．下列四个选项，正确的是（ ）
A．B．C．D．
3．如图，中，垂直平分于点，则的长为（ ）
A．B．C．D．
4．如图，为的直径，弦交于点，，，，则（ ）
A．B．C．1D．2
5．如图，OA是半⊙O的半径，弦BC⊥OA于点E，连接OC，若⊙O的半径为m，∠AOC＝∠α，则下列结论一定成立的是（ ）
A．OE＝m•tanαB．BC＝2m•sinα
C．AE＝m•csαD．S△COB＝m2•sinα
6．如图，在中，，为上一点，，，．则＝_____．
7．如图，在中，，于点D，，，则BC的值为______________.
8．如图，等边三角形ABC内接于⊙O，BC=2，则图中阴影部分的面积是________．
9．如图，已知Rt△ABC 中，∠C=90°，AD为∠BAC的平分线，且AD=2，AC=，解这个直角三角形．
10．已知：如图在△ABC中，AD是边BC上的高，E为边AC的中点，BC＝14，AD＝12，．求：
(1)线段DC的长；
(2)tan∠EDC的值．
题组C 培优拔尖练
1．如图，网格中小正方形的边长均为1，△ABC的顶点都在格点上，则cs∠BAC等于（ ）
A．B．C．D．
2．如图，在中，．作交边于点E，连接，则的值为（ ）
A．B．C．D．
3．如图，在正方形ABCD中，E，F分别为BC，CD的中点，点G在CD边上，，AG交BF于点H，连接．下列结论：①；②；③；④，其中正确的结论有（ ）
A．4个B．3个C．2个D．1个．
4．如图，△ABC中，∠C=90°，点O在AB上，以点O为圆心，OA为半径的半圆O与直角边BC相切于点F，分别交AC、AB于点D、E．已知CD=1，，则图中阴影部分的面积是（ ）
A．B．C．D．
5．已知：如图，AB=BC，∠ABC=90°，以AB为直径的⊙O交OC于点D，AD的延长线交BC于点E，过D作⊙O的切线交BC于点F．下列结论：①；②；③；④其中正确的有（ ）
A．①②③B．②③④C．①②④D．①③④
6．如图所示，点A与点B是两个四分之一圆的圆心，且两个圆的半径分别为3和6，则图中阴影部分的面积是___________．
7．如图，在中，AB是的直径，，AD，BC交于点E，点D为的中点，点G为平面内一动点，且，则AG的最小值为__________．
8．如图，的直径为，弦为，，则_____．
9．如图，在矩形ABCD中，对角线AC，BD相交于点O，AE垂直平分BO，交BD于点E，若AE，则矩形ABCD的周长为 _____．
10．如图，已知AB是的直径，为的内接三角形，C为BA延长线上一点，连接CD，于点E，交CD于点F，．
(1)求证：CD是的切线．
(2)若，求的长．
11．如图，在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过点D作直线DE⊥AC于点E
(1)求证，直线DE是⊙O的切线；
(2)尺规作图：过点B作直线DE的垂线，垂足为点F，（不写作法，保留作图痕迹）；
(3)若⊙O的半径为5，AD=8，求BF的长．
12．某数学社团遇到这样一个题目如图①，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=，BO∶CO=1∶3，求AB的长．经过社团成员讨论发现，如图②，过点B作BDAC，交AO的延长线于点D，通过构造△ABD 就可以解决问题．
(1)请写出求AB长的过程．
(2)如图③，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，∠ABC=∠ACB=75°，BO∶OD=1∶3．若AO=，求AB的长．
13．如图，直线经过上的点C，并且，，交直线于E、D，连，．
(1)求证：直线是的切线；
(2)试猜想，，三者之间的等量关系，并加以证明；
(3)若，的直径为5，求的长．
课程标准
课标解读
1.了解解直角三角形的含义，会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形。
2.会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题。
1.了解解直角三角形的概念，能运用直角三角形的角与角(两锐角互余)，边与边(勾股定理)、边与角关系解直角三角形。
2.运用直角三角形的角与角(两锐角互余)，边与边(勾股定理)、边与角关系解直角三角形。
已知条件
解法步骤
Rt△ABC
两
边
两直角边(a，b)
由求∠A，
∠B=90°－∠A，
斜边，一直角边(如c，a)
由求∠A，
∠B=90°－∠A，
一
边
一
角
一直角边
和一锐角
锐角、邻边
(如∠A，b)
∠B=90°－∠A，
，
锐角、对边
(如∠A，a)
∠B=90°－∠A，
，
斜边、锐角(如c，∠A)
∠B=90°－∠A，
，