2022-2023学年辽宁省沈阳市浑南区八年级（上）期中数学试卷

这是一份2022-2023学年辽宁省沈阳市浑南区八年级（上）期中数学试卷，共22页。试卷主要包含了选择题等内容，欢迎下载使用。
1．在平面直角坐标系中，点A（2，﹣3）位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．下列各数，是无理数的为（ ）
A．0B．
C．D．2.626 266 62
3．若函数y＝（m﹣1）x|m|﹣5是一次函数，则m的值为（ ）
A．±1B．﹣1C．1D．2
4．小明在一个矩形的水池里游泳，矩形的长、宽分别为30米、40米，小明在水池中沿直线最远可以游（ ）
A．30米B．40米C．50米D．60米
5．下列语句：
①点（3，2）与点（2，3）是同一个点；
②点（0，﹣2）在x轴上；
③点（0，0）是坐标原点；
④点（﹣5，﹣6）到x轴的距离为6．其中，正确的有（ ）
A．0个B．1个C．2个D．3个
6．如图，在一块四边形ABCD空地中植草皮，测得AB＝3m，DA＝13m，CD＝12m，则需要（ ）元投入．
A．16800B．7200C．5100D．无法确定
7．设6﹣的整数部分为a，小数部分为b，则（2a+）（ ）
A．6B．2C．12D．9
8．在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y轴距离为4（ ）
A．y＝B．y＝﹣C．y＝D．y＝﹣
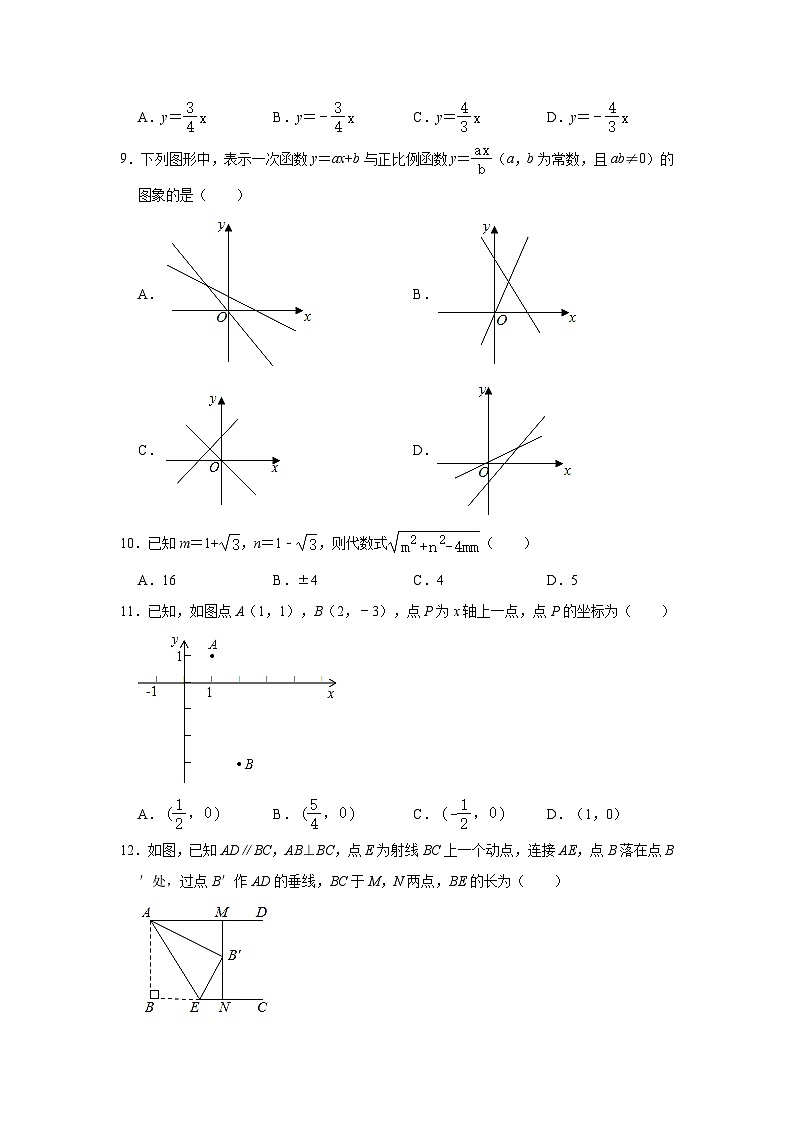
9．下列图形中，表示一次函数y＝ax+b与正比例函数y＝（a，b为常数，且ab≠0）的图象的是（ ）
A．B．
C．D．
10．已知m＝1+，n＝1﹣，则代数式（ ）
A．16B．±4C．4D．5
11．已知，如图点A（1，1），B（2，﹣3），点P为x轴上一点，点P的坐标为（ ）
A．B．C．D．（1，0）
12．如图，已知AD∥BC，AB⊥BC，点E为射线BC上一个动点，连接AE，点B落在点B′处，过点B′作AD的垂线，BC于M，N两点，BE的长为（ ）
A．B．C．或D．或
二.填空愿：本大题共8小题，每小题4分，共32分（请将答案坝写在图中横）上）
13．（4分）125的立方根是 ．
14．（4分）如果点A（4，y）与B（x，﹣4）关于y轴对称，则＝ ．
15．（4分）若y关于x的一次函数y＝﹣2mx﹣（m2﹣4）的图象过原点，且y随x的增大而增大，则m＝ ．
16．（4分）已知最简根式4与是同类二次根式，则a+b＝ ．
17．（4分）已知直线y＝kx+b平行于直线y＝﹣7x+4，且在y轴上的截距为﹣1，那么该直线的解析式是 ．
18．（4分）如图，三角形ABC中，∠ACB＝90°，BC＝4，P为直线AB上一动点，则线段PC的最小值是 ．
19．（4分）已知点A（﹣2，0），点P是直线y＝x上的一个动点，O，P为顶点的三角形面积是3时，点P的坐标为 ．
20．（4分）如图，矩形ABCD中，AB＝8，P为AD上一点，将△ABP沿BP翻折至△EBP，且OE＝OD，则AP的长为 ．
三.解答题：（本大题共5小题，共52分）
21．（20分）计算题：
（1）×；
（2）（）2﹣（2）（2﹣）；
（3）（2）（）﹣×；
（4）（﹣2）（2）﹣（﹣）2×；
（5）（3﹣2+）÷2+（）2．
22．（8分）现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，已知消防车高3m，救人时云梯伸至最长如图，云梯先在A处完成从9m高处救人后
（1）DM＝ 米，BB'＝ 米；
（2）①求消防车在A处离楼房的距离（AD的长度）；
②求消防车两次救援移动的距离（AB的长度）．
（精确到0.1m，参考数据≈1.73，≈3.16，≈4.36）
23．（6分）如图，已知直线y＝﹣2x+4．
（1）求该直线与x轴、y轴的交点A，B的坐标；
（2）若该直线上有一点C（﹣3，n），求△OAC的面积．
24．（6分）我们规定：在平面直角坐标系xOy中，任意不重合的两点M（x1，y1），N（x2，y2）之间的“折线距离”为d（M，N）＝|x1﹣x2|+|y1﹣y2|．例如图1中，点M（﹣2，3）与点N（1，﹣1）（M，N）＝|﹣2﹣1|+|3﹣（﹣1）|＝3+4＝7．
根据上述知识，解决下面问题：
（1）已知点P（3，﹣4），在点A（5，2），B（﹣1，0），C（﹣2，1），D（0，1）中，与点P之间的“折线距离”为8的点是 ；
（2）如图2，已知点P（3，﹣4），若点Q的坐标为（t，2）（P，Q）＝10，求t的值；
（3）如图2，已知点P（3，﹣4），若点Q的坐标为（t，t+1）（P，Q）＝8，直接写出t的取值范围．
25．（12分）如图（1），在平面直角坐标系中，直线，过点C（﹣4，0）作CD交AB于D
（1）求B点坐标为 ；线段OA的长为 ；
（2）确定直线CD解析式，求出点D坐标；
（3）如图2，点M是线段CE上一动点（不与点C、E重合），ON⊥OM交AB于点N
①点M移动过程中，线段OM与ON数量关系是否不变，猜想并证明；
②当△OCM和△OAN面积相等时，求点N的坐标．
2022-2023学年辽宁省沈阳市浑南区东北育才外国语学校八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（共12小题，每小题3分，满分36分）
1．在平面直角坐标系中，点A（2，﹣3）位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】D
解：点A坐标为（2，﹣3），纵坐标为负，
故选：D．
2．下列各数，是无理数的为（ ）
A．0B．
C．D．2.626 266 62
【答案】见试题解答内容
解：0是有理数，故A选项不符合题意；
是有理数，故B选项不符合题意；
是无理数，故C选项符合题意；
2.62626662是有理数，故D选项不符合题意；
故选：C．
3．若函数y＝（m﹣1）x|m|﹣5是一次函数，则m的值为（ ）
A．±1B．﹣1C．1D．2
【答案】B
解：根据题意得，|m|＝1且m﹣1≠6，
解得m＝±1且m≠1，
所以，m＝﹣8．
故选：B．
4．小明在一个矩形的水池里游泳，矩形的长、宽分别为30米、40米，小明在水池中沿直线最远可以游（ ）
A．30米B．40米C．50米D．60米
【答案】C
解：小明在水池中沿直线最远可以游AC＝＝50（米），
故选：C．
5．下列语句：
①点（3，2）与点（2，3）是同一个点；
②点（0，﹣2）在x轴上；
③点（0，0）是坐标原点；
④点（﹣5，﹣6）到x轴的距离为6．其中，正确的有（ ）
A．0个B．1个C．2个D．3个
【答案】C
解：①点（3，2）与点（4，横纵坐标不同；
②点（0，﹣2）在y轴上；
③点（8，0）是坐标系的原点；
④点（﹣5，﹣4）到x轴的距离为6．
故选：C．
6．如图，在一块四边形ABCD空地中植草皮，测得AB＝3m，DA＝13m，CD＝12m，则需要（ ）元投入．
A．16800B．7200C．5100D．无法确定
【答案】B
解：连接AC，
因为AB＝3m，BC＝4m，CD＝12m，
所以AC3＝AB2+BC2，
＝42+35，
＝16+9，
＝25，
所以AC＝5m，
又因AD8﹣DC2，
＝132﹣122，
＝169﹣144，
＝25，
＝AC2，
所以△DAC为直角三角形，
因此S四边形ABCD的面积＝S△ABC+S△DAC，
＝AB×BC+，
＝×4×2+，
＝7+30，
＝36．
故费用为：200×36＝7200元，
故选：B．
7．设6﹣的整数部分为a，小数部分为b，则（2a+）（ ）
A．6B．2C．12D．9
【答案】A
解：∵3＜＜4，
∴7＜6﹣＜3，
∵7﹣的整数部分为a，
∴a＝2，b＝6﹣，
∴（4a+）b＝（2×2+）＝（7+）＝6，
故选：A．
8．在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y轴距离为4（ ）
A．y＝B．y＝﹣C．y＝D．y＝﹣
【答案】B
解：∵点M到x轴的距离为3，到y轴距离为4，
∴M（﹣8，3），
设OM的解析式为y＝kx+b，
将点O（0，6），3）代入，得
，
∴，
∴y＝﹣x，
故选：B．
9．下列图形中，表示一次函数y＝ax+b与正比例函数y＝（a，b为常数，且ab≠0）的图象的是（ ）
A．B．
C．D．
【答案】A
解：若a＞0，b＞0，
则函数y＝ax+b图象经过一、二、三象限图象经过一，
若a＞8，b＜0，
则函数y＝ax+b图象经经过一、三、四象限图象经过二，
若a＜0，b＜4
则函数y＝ax+b图象经经过二、三、四象限图象经过一，
若a＜0，b＞0
则函数y＝ax+b图象经经过一、二、四象限图象经过二，
故选：A．
10．已知m＝1+，n＝1﹣，则代数式（ ）
A．16B．±4C．4D．5
【答案】C
解：∵m＝1+，n＝2﹣，
∴m+n＝1++1﹣，mn＝（7+）＝82﹣（）2＝1﹣3＝﹣3，
∴原式＝＝＝＝4．
故选：C．
11．已知，如图点A（1，1），B（2，﹣3），点P为x轴上一点，点P的坐标为（ ）
A．B．C．D．（1，0）
【答案】A
解：作A关于x轴对称点C，连接BC并延长交x轴于点P，
∵A（1，1），
∴C的坐标为（4，﹣1），
连接BC，
设直线BC的解析式为：y＝kx+b，
∴，
解得：，
∴直线BC的解析式为：y＝﹣2x+1，
当y＝3时，x＝，
∴点P的坐标为：（，0），
∵当B，C，P不共线时，
∴此时|PA﹣PB|＝|PC﹣PB|＝BC取得最大值．
故选：A．
12．如图，已知AD∥BC，AB⊥BC，点E为射线BC上一个动点，连接AE，点B落在点B′处，过点B′作AD的垂线，BC于M，N两点，BE的长为（ ）
A．B．C．或D．或
【答案】D
解：①当MB'＝MN时
Rt△AMB'中，AB'＝AB＝6AB＝3，
∴AM＝＝2，
∵AD∥BC，AB⊥BC，
∴四边形ABNM是矩形，
∴BN＝AM＝2，MN＝AB＝3，
设BE＝x，则B'E＝x﹣x，
Rt△B'EN中，B'N＝MN﹣MB'＝32+B'N2＝B'E6，
∴（2﹣x）4+22＝x7，
解得x＝，
∴BE的长为；
②当NB'＝MN时
∵NB'＝MN＝1，
∴MB'＝7，
设BE＝y，
同①可得y＝，
∴BE的长为，
综上所述，BE的长为或．
故选：D．
二.填空愿：本大题共8小题，每小题4分，共32分（请将答案坝写在图中横）上）
13．（4分）125的立方根是 5 ．
【答案】见试题解答内容
解：∵53＝125，
∴125的立方根是4，
故答案为5．
14．（4分）如果点A（4，y）与B（x，﹣4）关于y轴对称，则＝ 4 ．
【答案】4．
解：∵点A（4，y）与B（x，
∴x＝﹣4，y＝﹣5，
∴＝＝4．
故答案为：4．
15．（4分）若y关于x的一次函数y＝﹣2mx﹣（m2﹣4）的图象过原点，且y随x的增大而增大，则m＝ ﹣2 ．
【答案】﹣2．
解：∵y关于x的一次函数y＝﹣2mx﹣（m2﹣7）的图象过原点，且y随x的增大而增大，
∴﹣2m＞0，且6＝0﹣（m2﹣8），
∴m＝±2，
∵﹣2m＞4，
∴m＝﹣2．
故答案为：﹣2．
16．（4分）已知最简根式4与是同类二次根式，则a+b＝ 5 ．
【答案】见试题解答内容
解：由最简根式，同类二次根式的概念得：2a+b＝7，b＝3，
所以a+b＝5，
故答案为：5．
17．（4分）已知直线y＝kx+b平行于直线y＝﹣7x+4，且在y轴上的截距为﹣1，那么该直线的解析式是 y＝﹣7x﹣1 ．
【答案】见试题解答内容
解：∵直线y＝kx+b平行于直线y＝﹣7x+4，
∴k＝﹣7．
又∵直线y＝kx+b在y轴上的截距为﹣1，
∴b＝﹣1，
∴这条直线的解析式是y＝﹣8x﹣1．
故答案为：y＝﹣7x﹣7．
18．（4分）如图，三角形ABC中，∠ACB＝90°，BC＝4，P为直线AB上一动点，则线段PC的最小值是 ．
【答案】见试题解答内容
解：作CP⊥AB于P，
由垂线段最短可知，此时PC最小，
由勾股定理得，AB＝＝，
S△ABC＝×AC×BC＝，即×3×4＝，
解得，PC＝，
故答案为：．
19．（4分）已知点A（﹣2，0），点P是直线y＝x上的一个动点，O，P为顶点的三角形面积是3时，点P的坐标为 （4，3）或（﹣4，﹣3） ．
【答案】见试题解答内容
解：∵点P是直线y＝x上的一个动点，
∴可设P（x，x），
∵以A，O，P为顶点的三角形面积是3，
∴×AO×|，
即×4×|，
解得x＝±7，
∴P（4，3）或（﹣5，
故答案为：（4，3）或（﹣5．
20．（4分）如图，矩形ABCD中，AB＝8，P为AD上一点，将△ABP沿BP翻折至△EBP，且OE＝OD，则AP的长为 4.8 ．
【答案】见试题解答内容
解：设CD与BE交于点G，
∵四边形ABCD是矩形，
∴∠D＝∠A＝∠C＝90°，AD＝BC＝6，
由折叠的性质可知△ABP≌△EBP，
∴EP＝AP，∠E＝∠A＝90°，
在△ODP和△OEG中，
，
∴△ODP≌△OEG（ASA），
∴OP＝OG，PD＝GE，
∴DG＝EP，
设AP＝EP＝x，则PD＝GE＝6﹣x，
∴CG＝4﹣x，BG＝8﹣（6﹣x）＝5+x，
根据勾股定理得：BC2+CG2＝BG8，
即62+（5﹣x）2＝（x+2）2，
解得：x＝4.8，
∴AP＝6.8，
故答案为：4.2．
三.解答题：（本大题共5小题，共52分）
21．（20分）计算题：
（1）×；
（2）（）2﹣（2）（2﹣）；
（3）（2）（）﹣×；
（4）（﹣2）（2）﹣（﹣）2×；
（5）（3﹣2+）÷2+（）2．
【答案】（1）5+；
（2）﹣12；
（3）﹣1；
（4）0；
（5）5．
解：（1）×
＝4+﹣+2
＝4+﹣+5
＝5+；
（2）（）2﹣（5）（5﹣）
＝（）2﹣2×8+（4）2﹣（3）2+（）2
＝6﹣12+12﹣20+2
＝﹣12；
（3）（2）（×
＝（）2﹣52﹣+
＝3﹣8﹣+
＝﹣5；
（4）（﹣2）（8）4×
＝（）2﹣52﹣3+4×
＝5﹣4﹣8+2
＝0；
（5）（2﹣2++（）2
＝﹣++
＝×2﹣+
＝5．
22．（8分）现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，已知消防车高3m，救人时云梯伸至最长如图，云梯先在A处完成从9m高处救人后
（1）DM＝ 3 米，BB'＝ 10 米；
（2）①求消防车在A处离楼房的距离（AD的长度）；
②求消防车两次救援移动的距离（AB的长度）．
（精确到0.1m，参考数据≈1.73，≈3.16，≈4.36）
【答案】（1）3，10；
（2）①8m；②3.6m．
解：（1）由题意知，DM＝3m，
故答案为：3，10；
（2）①AA'＝10m，A'M＝8m，
∴A'D＝A'M﹣DM＝9﹣3＝7m，
在Rt△AA'D中，由勾股定理得，
AD＝＝7（m），
②在Rt△BB'D中，由勾股定理得＝≈4.36（m），
∴AB＝AD﹣BD＝7﹣4.36≈3.6（m），
∴消防车两次救援移动的距离为3.6m．
23．（6分）如图，已知直线y＝﹣2x+4．
（1）求该直线与x轴、y轴的交点A，B的坐标；
（2）若该直线上有一点C（﹣3，n），求△OAC的面积．
【答案】（1）A的坐标为（2，0），B的坐标为（0，4）；（2）10．
解：（1）令y＝0，则x＝2，则y＝3，
故函数图象与x轴的交点A的坐标为（2，0），
y轴的交点B的坐标为（2，4）；
（2）把x＝﹣3代入y＝﹣3x+4，
得：y＝6+2＝10，
∴C（﹣3，10），
S△OAC＝×2×10＝10．
24．（6分）我们规定：在平面直角坐标系xOy中，任意不重合的两点M（x1，y1），N（x2，y2）之间的“折线距离”为d（M，N）＝|x1﹣x2|+|y1﹣y2|．例如图1中，点M（﹣2，3）与点N（1，﹣1）（M，N）＝|﹣2﹣1|+|3﹣（﹣1）|＝3+4＝7．
根据上述知识，解决下面问题：
（1）已知点P（3，﹣4），在点A（5，2），B（﹣1，0），C（﹣2，1），D（0，1）中，与点P之间的“折线距离”为8的点是 A，B，D ；
（2）如图2，已知点P（3，﹣4），若点Q的坐标为（t，2）（P，Q）＝10，求t的值；
（3）如图2，已知点P（3，﹣4），若点Q的坐标为（t，t+1）（P，Q）＝8，直接写出t的取值范围．
【答案】（1）A，B，D．
（2）t＝﹣1或t＝7．
（3）﹣5≤t≤3．
解：（1）由题意得d（P，A）＝|3﹣5|+|﹣5﹣2|＝8，
d（P，B）＝|6﹣（﹣1）|+|﹣4﹣7|＝8，
d（P，C）＝|3﹣（﹣8）|+|﹣4﹣1|＝10，
d（P，D）＝|3﹣0|+|﹣4﹣5|＝8，
故答案为：A，B，D．
（2）d（P，Q）＝|3﹣t|+|﹣6﹣2|＝10，
解得t＝﹣1或t＝5．
（3）d（P，Q）＝|3﹣t|+|﹣4﹣（t+5）|，
化简得d（P，Q）＝|3﹣t|+|5+t|，
当﹣8≤t≤3时，|3﹣t|+|4+t|＝3﹣t+5+t＝3．
当t＜﹣5时，|3﹣t|+|4+t|＝3﹣t﹣5﹣t＝﹣7﹣2t．
当t＞3时，|3﹣t|+|5+t|＝t﹣3+8+t＝2+2t．
∴﹣6≤t≤3．
25．（12分）如图（1），在平面直角坐标系中，直线，过点C（﹣4，0）作CD交AB于D
（1）求B点坐标为 （0，4） ；线段OA的长为 3 ；
（2）确定直线CD解析式，求出点D坐标；
（3）如图2，点M是线段CE上一动点（不与点C、E重合），ON⊥OM交AB于点N
①点M移动过程中，线段OM与ON数量关系是否不变，猜想并证明；
②当△OCM和△OAN面积相等时，求点N的坐标．
【答案】（1）（0，4），3；
（2）点D的坐标为（，）；
（3）①点M移动过程中，线段OM与ON数量关系不变，证明见解析；
②点N的坐标为（，2）．
解：（1）∵直线y＝﹣x+8交坐标轴于A，
∴当y＝0时，x＝3，y＝7，
∴点A的坐标为（3，0），2），
∴OA＝3；
故答案为：（0，6），3；
（2）∵过点C（﹣4，7）作CD交AB于D．且△COE≌△BOA（已知），
∴OC＝4，OC＝OB，
∵点A（3，7），
∴OA＝3，
∴OE＝3，
∴点E的坐标为（8，3），
设过点C（﹣4，2），3）的直线解析式为y＝kx+b，
∴，解得，
∴直线CE的解析式为y＝x+3，
即直线CD的解析式为y＝x+3，
由，得，
即点D的坐标为（，）；
（3）①线段OM与ON数量关系是OM＝ON保持不变，
证明：∵△COE≌△BOA，
∴OE＝OA，∠OEM＝∠OAN，
∵∠BOA＝90°，ON⊥OM，
∴∠MON＝∠BOA＝90°，
∴∠MOE+∠EON＝∠EON+∠NOA，
∴∠MOE＝∠NOA，
在△MOE和△NOA中，
，
∴△MOE≌△NOA（ASA），
∴OM＝ON，
即线段OM与ON数量关系是OM＝ON保持不变；
②∵△MOE≌△NOA，△COE≌△BOA，
∴△MOE与△NOA面积相等，△COE与△BOA面积相等，
∴△BON与△OCM面积相等，
∵△OCM和△OAN面积相等，
∴△BON与△OAN面积相等，
即△OAN面积是△AOB面积的一半，
∴OA•yN＝×OA•OB，
∴×3×yN＝××3×4，
解得：yN＝2，
把y＝7代入y＝﹣x+4，
解得：x＝，
∴点N的坐标为（，2）．