吉林省长春市南关区2023-2024学年九年级上学期12月月考数学模拟试题（含答案）

这是一份吉林省长春市南关区2023-2024学年九年级上学期12月月考数学模拟试题（含答案），共13页。试卷主要包含了12，已知函数等内容，欢迎下载使用。
本试卷包括三道大题，共24道小题，共6页，全卷满分120分，考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回．
注意事项：
1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．
2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试卷上答题无效．
一、选择题（本大题共8小题，每小题3分，共24分）
1．等于（）
（A）4．（B）-4．（C）．（D）2．
2．下列二次根式中，是最简二次根式的是（）
（A）．（B）．（C）．（D）．
3．已知关于x的一元二次方程有一个根是0，则m的值为（）
（A）．（B）-2．（C）2．（D）0．
4．若，则等于（）
（A）．（B）．（C）．（D）．
5．如图，，直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F，若，，，则AC的长是（）
（第5题）
（A）6．（B）8．（C）9．（D）12．
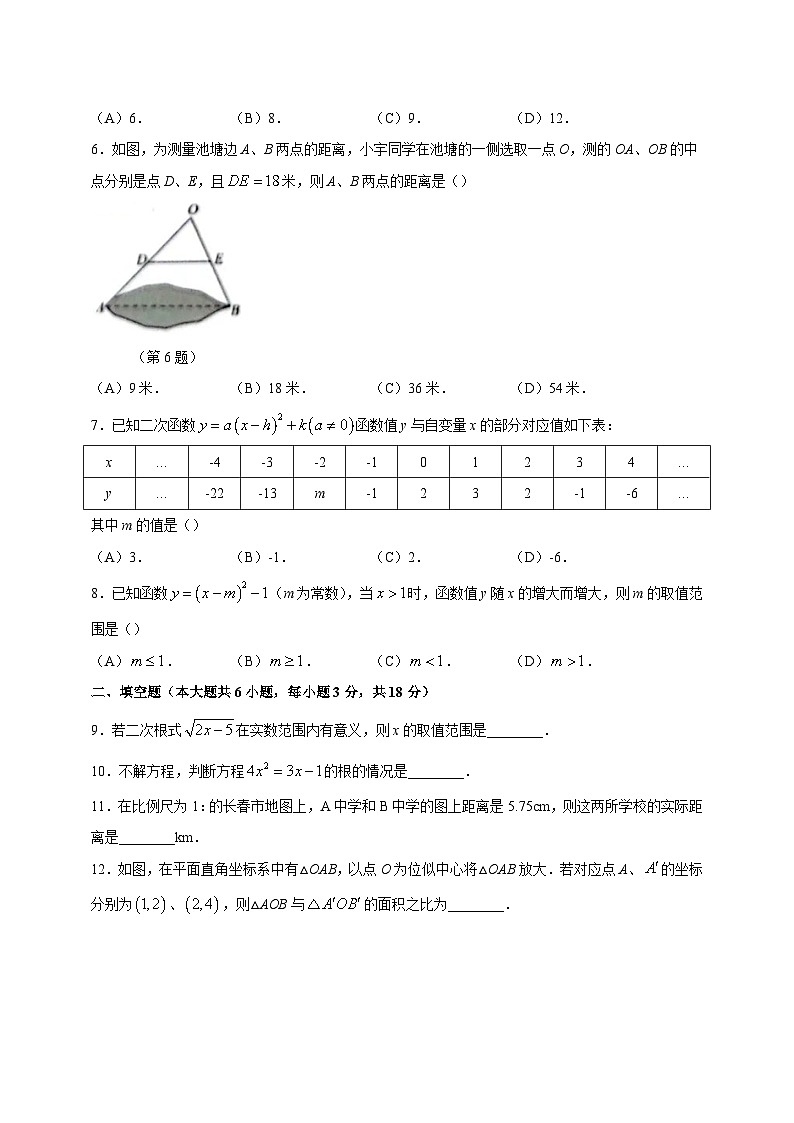
6．如图，为测量池塘边A、B两点的距离，小宇同学在池塘的一侧选取一点O，测的OA、OB的中点分别是点D、E，且米，则A、B两点的距离是（）
（第6题）
（A）9米．（B）18米．（C）36米．（D）54米．
7．已知二次函数函数值y与自变量x的部分对应值如下表：
其中m的值是（）
（A）3．（B）-1．（C）2．（D）-6．
8．已知函数（m为常数），当时，函数值y随x的增大而增大，则m的取值范围是（）
（A）．（B）．（C）．（D）．
二、填空题（本大题共6小题，每小题3分，共18分）
9．若二次根式在实数范围内有意义，则x的取值范围是________．
10．不解方程，判断方程的根的情况是________．
11．在比例尺为1：的长春市地图上，A中学和B中学的图上距离是5.75cm，则这两所学校的实际距离是________km．
12．如图，在平面直角坐标系中有△OAB，以点O为位似中心将△OAB放大．若对应点A、的坐标分别为、，则△AOB与的面积之比为________．
（第12题）
13．如图，在正方形ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．若，则OF的长为________．
（第13题）
14．如图，在平面直角坐标系中，抛物线交x轴正半轴于点C，交y轴于点A，轴交抛物线于点B，则△ABC的面积是________．
（第14题）
三、解答题（本大题共10小题，共78分）
15．（6分）计算：．
16．（6分）求证：对于任意实数m，关于x的方程总有两个不相等的实数根．
17．（6分）通过配方，写出抛物线的开口方向、对称轴和顶点坐标．
18．（7分）如图，在灯塔A周围20海里水域有暗礁．一艘由西向东航行的轮船航行到O处发现，灯塔A在轮船的北偏东63°的方向上，且与轮船相距52海里．若该轮船不改变航向，通过计算说明该轮船是否有触暗礁的危险．【参考数据：，，】
19．（7分）图①、图②、图③均是的正方形网格，毎个小正方形的顶点称为格点，点A、B均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，不要求写画法，要求保留必要的作图痕迹．
图①图②图③
（第19题）
（1）在图①中以线段AB为边画△ABC，使点C在格点上，且．
（2）在图②中以线段AB为边画△ABD，使．
（3）在图③中以线段AB为边画△ABE，使面积为3个平方单位．
20．（7分）如图，点E在矩形ABCD的BC边上，将沿AE翻折得到△AEF，过点F作，交BC、AD于点P、Q．
（第20题图）
（1）求证：．
（2）已知，若△AEF与△AFQ相似，直接写出BE的长．
21．（8分）为了提升居民生活质量，完善社区公共区域配套设施，今年夏天长春市在多个城区实施了旧城改造工程．已知某工程队在开始施工的7月份为某小区翻新道路，为了在入冬前完成道路翻新工程，之后加快了工程进度，结果9月份为该小区翻新道路．
（1）求这两个月该工程队工作效率的月平均增长率．
（2）若10月份该工程队的工作效率按此增长率增长，估计到10月末该工程队能否完成该小区共的道路翻新任务？
22．（9分）两千多年前，古希腊数学家欧多克索斯发现：将一条线段AB分割成长、短两条线段AP、PB，若，则把这种分割叫做黄金分割，点P叫做线段AB的黄金分割点，这个比值叫做黄金比．
图①图②图③
（1）如图①，点P是线段AB的黄金分割点，设，，求黄金比x的值．
（精确到0.001，参考数据：，，，）
（2）如图②，在△ABC中，，，BD是△ABC的角平分线．
求证：点D是线段AC的黄金分割点．
（3）如图③，点E是正方形ABCD的BC边的中点，以点E为圆心以ED长为半径画弧，交射线BC于点F，过点F作交射线AD于点G．若，请直接写出AB的长．
23．（10分）法国数学家韦达在研究一元二次方程时发现：如果关于x的一元二次方程的两个实数根分别为、，那么，．习惯上把这个结论称作“韦达定理”．
（1）方程的两个实数根分别为、，求和的值．
（2）方程的两个实数根分别为、，求的值．
（3）若、为关于x的方程的两个实数根，求的最小值．
24．（12分）如图，在□ABCD中，，，．动点P从点B出发，先沿以每秒5个单位长度的速度运动，然后沿以每秒10个单位长度的速度继续运动．与此同时，动点Q从点B出发，沿BC方向以每秒5个单位长度的速度运动．当其中一点到达终点时，P、Q两点同时停止运动．设运动时间为t（秒），连结PQ．
（第24题）（备用图）
（1）当点P沿运动时，求AP的长（用含t的代数式表示）．
（2）当时，求t的值．
（3）连结AQ，当△APQ的面积等于8个单位面积时，求t的值．
（4）当点P在线段AD上时，把四边形PQBA沿PQ翻折得到四边形，直接写出时t的值．
数学答案
一、1．A2．D3．B4．B5．C6．C7．D8．A
二、9．．10．没有实数根．11．11.5．
12．1：4．13．1．14．2．
三、15．解：
（3分）
（4分）
（6分）
16．（1分）
（2分）
．（3分）
∵，（4分）
∴．（5分）
∴对于任意实数m，关于x的方程总有两个不相等的实数根．（6分）
17．解：，（3分）
∵，
∴抛物线的开口向下，（4分）
对称轴为直线，顶点坐标为．（6分）
18．解：过A点作．（1分）
在Rt△AOC中，
∵，
，（3分）
∴（4分）
（5分）
．（6分）
∴该轮船没有触暗礁的危险．（7分）
（第18题）
19．（1）（2分）
（2）（4分）
（第19题）
（3）（7分）
20．（1）证明：∵四边形ABCD是矩形，
∴．（1分）
∵，
∴．（2分）
∴．
又由翻折可知，．（3分）
∴．
∴．（4分）
∴．（5分）
（2）．（7分）
（第20题）
21．（1）解：设该工程队工作效率的月平均增长率为x，（1分）
根据题意，得．（3分）
解这个方程，得，（不合题意舍去）．（5分）
答：该工程队工作效率的月平均增长率为10%．（6分）
（2）8月的工程量为：；10月的工程量为：；（7分）
．
所以该工程队能完成该小区的道路翻新任务．（8分）
22．（1）根据题意得，．（1分）
解得，（舍），．（3分）
（2）∵，，
∴．（4分）
∵BD是△ABC的角平分线，
∴．
∴，且．
∴，．（5分）
（第22题）
又∵，
∴．
∴．（6分）
∴点D是线段AC的黄金分割点．（7分）
（3）．（注：得2.764给满分）（9分）
23．解：（1），．（2分）
（2），．（3分）
．（6分）
（3）∵方程有两个实数根，
∴，．（7分）
∵，，（8分）
∴
．（9分）
∵，
∴时，有最小值，最小值为．（10分）
24．（1）如图③，时，；（1分）
如图①，时，．（2分）
（2）如图①，时，，；（3分）
如图②，时，，．（4分）
图①
图②
图③
（第24题）
（3）如图③，时，，（5分）
，．（7分）
如图①，时，，．（9分）
如图②，时，，（舍）．（10分）
（4），．（12分）
如图④，，．
如图⑤，
，，
，，
，，
，．
图④
图⑤
图⑥
解法二：（手绘不准确图）如图⑥，
当时，，，．
，，．
，△ABE中，，．
当时，，，．
，△ABE中，，．x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
-22
-13
m
-1
2
3
2
-1
-6
…