

精品解析:甘肃省酒泉市第二中学2022-2023学年九年级上学期期末考试数学试题(解析版)
展开
这是一份精品解析:甘肃省酒泉市第二中学2022-2023学年九年级上学期期末考试数学试题(解析版),共21页。试卷主要包含了选择题,综合题等内容,欢迎下载使用。
(满分:120分 时间:120分钟)
一、选择题(本大题共10个小题,每小题3分,满分30分)
1. 下列一元二次方程中,没有实数根的是( )
A. B.
C. D.
【答案】A
【解析】
【详解】A.∵△=25﹣4×2×4=﹣7<0,∴方程没有实数根,故本选项正确;
B.∵△=36﹣4×1×4=0,∴方程有两个相等的实数根,故本选项错误;
C.∵△=16﹣4×5×(﹣1)=36>0,∴方程有两个相等的实数根,故本选项错误;
D.∵△=16﹣4×1×3=4>0,∴方程有两个相等的实数根,故本选项错误;
故选:A.
【点睛】考点:根的判别式.
2. 已知为锐角,且,那么的度数是( )
A B. C. D.
【答案】D
【解析】
【分析】根据特殊角的三角函数值求解即可.
【详解】解∶∵为锐角,,
∴.
故选:D
【点睛】本题主要考查了特殊角的三角函数值,熟练掌握相关数值是解题关键.
3. 如图,已知直线,,,,则的长为( )
A. 2B. 4.5C. 6D. 8
【答案】B
【解析】
【分析】由直线,根据平行线分线段成比例定理,则,即可求得EF的长度.
【详解】解:∵,
∴,
∵,,,
∴,
故选择:B.
【点睛】此题考查了平行线分线段成比例定理.题目比较简单,解题的关键是注意数形结合思想的应用.
4. 某旅游景点的游客人数逐年增加,据有关部门统计,2015年约为12万人次,若2017年约为17万人次,设游客人数年平均增长率为x,则下列方程中正确的是( )
A. 12(1+x)=17
B. 17(1﹣x)=12
C. 12(1+x)2=17
D. 12+12(1+x)+12(1+x)2=17
【答案】C
【解析】
【分析】设游客人数的年平均增长率为x,由2015年约为12万人次,到2017年约为17万人次,增长了2次,可列出方程.
【详解】设游客人数的年平均增长率为x,由2015年约为12万人次,到2017年约为17万人次,增长2次,可列出方程12(1+x)2=17.
故选C
【点睛】本题考核知识点:列一元二次方程解应用题.解题关键点:找出相等关系,列方程.
5. 准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )
A. B. C. D.
【答案】C
【解析】
【分析】列出所有可能出现的牌面数字解题即可.
【详解】列举所有可能出现的牌面数字有(0,0) ,(0,1),(0,1),(1,1),
所以P==.
【点睛】本题考查用列举法求简单事件的概率.正确列出所有可能出现的情况是解题的关键.
6. 抛物线的顶点坐标是( )
A. B. C. D.
【答案】D
【解析】
【分析】由抛物线顶点式即可求解.
【详解】解:∵抛物线的顶点坐标是,
∴抛物线的顶点坐标是,
故选:D.
【点睛】本题考查二次函数的性质,解题关键是掌握抛物线的顶点坐标是.
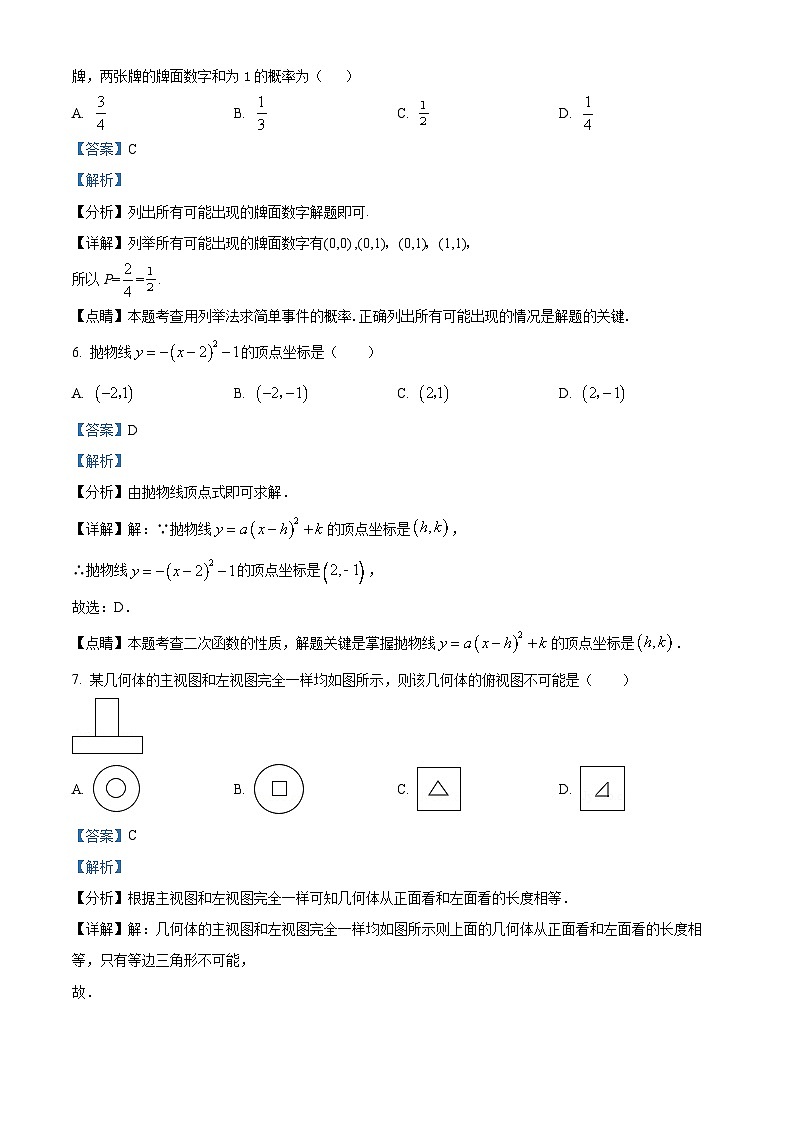
7. 某几何体的主视图和左视图完全一样均如图所示,则该几何体的俯视图不可能是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据主视图和左视图完全一样可知几何体从正面看和左面看的长度相等.
【详解】解:几何体的主视图和左视图完全一样均如图所示则上面的几何体从正面看和左面看的长度相等,只有等边三角形不可能,
故.
【点睛】本题考查简单空间图形的三视图,考查根据作三视图的规则来作出三个识图的能力,三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐;左视、俯视宽相等”.
8. 在△ABC中,D.E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
A. 8B. 12C. 16D. 20
【答案】C
【解析】
【详解】试题分析:∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴DE∥BC,,∴△ADE∽△ABC,∴,∵△ADE的面积为4,∴,∴S△ABC=16.故选C.
考点:1.相似三角形的判定与性质;2.三角形中位线定理.
9. 已知点在反比例函数的图象上,过P作x轴的垂线,垂足为M,则的面积为( )
A. 8B. 4C. 2D. 1
【答案】D
【解析】
【分析】先根据待定系数法求得k的值,然后根据反比例函数k的几何意义即可得出:,代入求值即可.
【详解】解:∵点在反比例函数的图象上,
∴,
根据反比例函数k的几何意义可得:.
故选:D.
【点睛】此题考查了反比例函数的几何意义,属于基础题,关键是掌握在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是,且保持不变.
10. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为,且经过点(2,0).下列说法:①abc<0,②a﹣b=0,③4a+2b+c<0,④若(﹣2,y1)是抛物线上的两点,则y1<y2,其中说法正确的是( )
A. ①④B. ③④C. ①③④D. ①②
【答案】A
【解析】
【分析】①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号;
②根据对称轴求出b=-a;
③把x=2代入函数关系式,结合图象判断函数值与0的大小关系;
④求出点(-2,y1)关于直线x=的对称点的坐标,根据对称轴即可判断y1和y2的大小.
【详解】解:①∵二次函数的图象开口向下,
∴a<0,
∵二次函数的图象交y轴的正半轴于一点,
∴c>0,
∵对称轴是直线x=,
∴-=,
∴b=-a>0,
∴abc<0.故①正确;
②∵由①中知b=-a,
∴a+b=0,故②错误;
③把x=2代入y=ax2+bx+c得:y=4a+2b+c,
∵抛物线经过点(2,0),
∴当x=2时,y=0,即4a+2b+c=0.故③错误;
④∵(-2,y1)关于直线x=的对称点的坐标是(3,y1),
又∵当x>时,y随x的增大而减小,<3,
∴y1<y2.故④正确;
综上所述,正确的结论是①④.
故选:A.
【点睛】本题考查了二次函数的图象和系数的关系的应用,注意:当a>0时,二次函数的图象开口向上,当a<0时,二次函数的图象开口向下.
二.填空题(本大题共8小题,每小题3分,共24分)
11. 已知是关于的方程的一个根,则______.
【答案】2023
【解析】
【分析】先利用一元二次方程根的定义得到,然后利用整体代入的方法得到的值.
【详解】∵是关于的方程的一个根,
∴,
∴,
∴,
故答案为:2023
【点睛】本题考查了一元二次方程的解:掌握能使一元二次方程左右两边相等的未知数的值是一元二次方程的解是解题的关键.
12. 已知,则的值为_______.
【答案】
【解析】
【分析】令连等式值为k,将a、b、c全部转化为用k表示的形式,进而得出比值.
【详解】令
则a=6k,b=5k,c=4k
则
故答案为:.
【点睛】本题考查连比式的应用,是一类比较常见的题型,需掌握这种解题方法.
13. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,CD=6,则AB=____.
【答案】12
【解析】
【分析】根据直角三角形斜边上中线等于斜边上的一半可求解.
【详解】解:在Rt△ABC中,∠ACB=90°,点D是AB的中点,CD=6,
∴AB=2CD=12.
故答案为:12.
【点睛】本题主要考查直角三角形斜边上的中线,掌握直角三角形斜边上的中线的性质是解题的关键.
14. 抛物线和的图象形状相同,对称轴平行于y轴,顶点为,则该抛物线的解析式为_________.
【答案】
【解析】
【分析】根据抛物线和的图象形状相同,得出,根据顶点为,写出抛物线的解析式即可.
【详解】解:∵抛物线和的图象形状相同,
∴,
∵顶点为,
∴抛物线的解析式为.
故答案为:.
【点睛】本题主要考查了求抛物线的解析式,解题的关键是熟练掌握抛物线的性质,抛物线的顶点式.
15. 两位同学玩“石头、剪子、布”游戏,随机出手一次,两人手势相同的概率是___.
【答案】
【解析】
【分析】用列表法即可解决.
详解】列表如下:
事件总的可能结果数为9,手势相同的有3种,则两人手势相同的概率是.
故答案为:
【点睛】本题考查了用树状图或列表法求等可能事件的概率,根据概率计算公式,关键是由图或表中得到事件所有可能的结果数及事件发生的结果数.
16. △ABC的顶点都在方格纸的格点上,则sinA=_____.
【答案】
【解析】
【分析】在直角△ABD中利用勾股定理求得AD的长,然后利用正弦的定义求解.
【详解】
在直角△ABD中,BD=1,AB=2,
则AD===,
则sinA= ==
故答案是:.
17. 已知线段,C为线段AB的黄金分割点,则___________.
【答案】cm
【解析】
【分析】利用黄金分割的定义计算即可.
【详解】解:∵点C是线段AB的黄金分割点,且AC>BC,
∴
∴cm,
故答案为:cm.
【点睛】本题考查了黄金分割点的定义,若C为线段AB的黄金分割点,则,熟练应用黄金分割的性质列出方程是解题的关键.
18. 一次函数的图象与反比例函数的图象交于点,两点,则使的的取值范围是____.
【答案】或
【解析】
【分析】坐标为和的两点在双曲线上,联立并解可得、的值;设一次函数的解析式为:,代入数据,解可得一次函数的解析式;画出函数图象,根据函数的图象,可得答案.
【详解】解:把,分别代入,
得,,
解得,,
所以点坐标为,点坐标为,
把,代入得
,
解得,
所以这个一次函数的表达式为,
函数图象如图所示:
根据图象可知,使的的取值范围是或.
【点睛】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.注意结合题意,结合图象选用合适的方法解题.
三.解答题(请写出必要的计算步骤或证明过程,其中19题8分、20题4分、21题6分、22题6分、23题5分、24题5分,共34分)
19. 解一元二次方程:
(1)
(2)
【答案】(1);
(2)
【解析】
【分析】(1)利用因式分解法求解即可;
(2)移项后,利用因式分解法求解即可.
【小问1详解】
解:,
∴,
∴或,
∴;
【小问2详解】
解:,
整理得,
∴,
∴或,
∴.
【点睛】此题考查解一元二次方程,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.
20. 计算:2sin30°+4cs245°﹣3tan45°
【答案】0
【解析】
【分析】根据特殊角的三角函数值,即可解答.
【详解】解:原式
【点睛】考查了特殊角的三角函数值,属于识记性题目,基础题.
21. 如图,和是直立在地面上的两根立柱,已知,某一时刻在太阳光下的影子长.
(1)在图中画出此时在太阳光下的影子;
(2)在测量的影子长时,同时测量出,计算的长.
【答案】(1)见解析 (2)的长为
【解析】
【分析】(1)利用平行投影的性质得出即可;
(2)利用同一时刻物体影子与实际高度的比值相等进而得出答案.
【小问1详解】
如图所示:即为所求;
【小问2详解】
由题意可得:
,
解得:,
答:的长为.
【点睛】此题主要考查了平行投影,利用同一时刻物体影子与实际高度的比值相等解题是解题关键.
22. 如图,已知是矩形的边上一点,于,试说明:.
【答案】见解析
【解析】
【详解】解法一:矩形中,,,
.
,
,
.
.
解法二:矩形中,.
,,
,
.
23. 某班从3名男生和2名女生中随机抽出2人参加演讲比赛,请用树状图或者列表的方式求出所抽取的两名学生中至少有一名女生的概率.
【答案】
【解析】
【分析】根据题意画出树状图,根据树状图结合概率公式即可求解.
【详解】解:画树状图得,
由树状图得共有20种等可能结果,其中所抽取的两名学生中至少有一名女生共有14种结果,所以.
【点睛】本题考查了根据树状图或列表法求概率,熟知概率公式,正确画出树状图或列表,表示出所有等可能结果是解题关键.
24. 如图,海中有一个小岛,它的周围海里内有暗礁,今有货船由西向东航行,开始在岛南偏西的处,往东航行海里后到达该岛南偏西的处后,货船继续向东航行,你认为货船在航行途中有没有触礁的危险.
【答案】无触礁的危险,理由见解析
【解析】
【分析】作高AD,由题意可得∠ACD=60°,∠ABC=30°,进而得出∠ABC=∠BAC=30°,于是AC=BC=20海里,在Rt△ADC中,利用直角三角形的边角关系,求出AD与15海里比较即可.
【详解】解 :过点A作ADBC,垂足为D
∵∠ ABC= ∠ ACD=
∴∠ BAC==∠ ABC
∴BC=AC=20
∴ =
AD=20=10
所以货船在航行途中无触礁的危险.
【点睛】本题考查了解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,正确作出高线是解题的关键.
四、综合题(共32分,其中25题6分、26题8分、27题9分、28题9分)
25. 如图,一次函数与反比例函数的图像相较于,两点.
(1)求一次函数与反比例函数的解析式;
(2)过点作轴,垂足为,求.
【答案】(1);
(2)5
【解析】
【分析】(1)把的坐标代入反比例函数的解析式,求出其解析式,把的坐标代入反比例函数的解析式,求出的坐标,把、的坐标代入一次函数的解析式,得出方程组,求出方程组的解即可;
(2)求出,边上的高是,代入三角形的面积公式即可.
【小问1详解】
∵点)在的图像上,
∴,
∴反比例函数的解析式为:,
∴
∵点在的图像上,
∴,
∴,
∴一次函数的解析式为:;
【小问2详解】
以为底,则边上的高为3+2=5,
∴,
【点睛】本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数、反比例函数的解析式,三角形的面积的应用,主要培养学生分析问题和解决问题的能力,题型较好,难度适中.
26. 某种服装,平均每天可以销售20件,每件盈利44元.若每件降价1元,则每天可以多销售5件.
(1)如果每天要盈利1600元,每件应降多少元?
(2)问将售价降多少元时,才能使每天所赚的利润最大?并求出最大利润.
【答案】(1)36元或4元
(2)20元,2880元
【解析】
【分析】(1)设每件降价x元,则每件盈利元,平均每天可销售件,根据题意列出相应的方程,即可求得如果每天要赢利1600元,每件应降价多少元;
(2)设总利润为w元,根据题意可以得到利润与降价之间的函数关系式,然后根据二次函数的性质即可解答本题.
【小问1详解】
解:设每件降价x元,则每件盈利元,平均每天可销售件,
依题意得:,
整理得:,
解得:,,
∴每件应降价4元或36元.
【小问2详解】
解:设总利润为w元,
∵,
∵,
∴当时,w有最大值,此时元.
答:每件应降价20元,每天能获得最大利润,最大利润为2880元.
【点睛】本题考查了二次函数的应用、一元二次方程的应用,解答本题的关键是明确题意,利用方程的知识和二次函数的性质即可解答本题.
27. 如图,已知,直线垂直平分,与边交于,连接,过点作平行于交于点,连接.
(1)求证:;
(2)求证:四边形是菱形;
(3)若,,则菱形的面积是______.
【答案】(1)见解析;
(2)见解析; (3);
【解析】
【分析】(1)由为线段的垂直平分线,得到,再由,得到,则问题可证;
(2)由全等得到,再由线段垂直平分线性质得到,则可证明四边形四边相等,则求证可证明;
(3)利用勾股定理求出,进而得到菱形两条对角线,则菱形面积可求.
【小问1详解】
证明:由已知,为线段的垂直平分线,
,
∵,
∴,
在与中,
∴;
【小问2详解】
证明:∵;
∴,
∵为线段的垂直平分线,
∴,
∴,
∴四边形是菱形;
【小问3详解】
∵,,
∴,
∴,
∴菱形的面积是;
故答案为:
【点睛】本题考查了全等三角形的性质和判定、线段垂直平分线的性质和菱形的判定方法,解答关键是根据题意灵活的选择菱形的判定方法.
28. 如图,抛物线与x轴交于两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求抛物线关系式;
(2)的值
(3)点P为抛物线上一点,且,求点P的坐标.
【答案】(1)
(2)
(3)
【解析】
【分析】(1)用待定系数法求解即可;
(2)连接,过点D作于点E.求出点D和点C的坐标,则易知,所以.利用直角等腰直角三角形的性质和图中相关线段间的和差关系求得,.由正切三角函数定义知;
(3)过点P作轴于点F,易得,利用(2)中的结果得到:.设,则利用锐角三角函数定义推知,通过解方程求得点P的坐标为.
【小问1详解】
根据题意得,
解得:,
∴;
【小问2详解】
连接,,过点D作于点E.
把代入,得
,
∴.
把代入,得
,
∴,
∴,
∴.
在中,
∵,
∴.
在中,.
∴,
∴.
∴;
【小问3详解】
过点P作轴于点F.
∵,
∴,
∵,
∴.
设,则,
解得 (舍去),
把代入,得
,
∴.
【点睛】本题考查了坐标与图形性质,勾股定理,锐角三角函数定义以及二次函数图象上点的坐标特征等知识点.解题时,要注意数形结合的数学思想方法.石头
剪子
布
石头
石头,石头
石头,剪子
石头,布
剪子
剪子,石头
剪子,剪子
剪子,布
布
布,石头
布,剪子
布,布
相关试卷
这是一份甘肃省酒泉市玉门市第二中学九年级(上)学期期末数学试题(含解析),共14页。试卷主要包含了单项选择,填空题,解答题等内容,欢迎下载使用。
这是一份精品解析:甘肃省嘉峪关市实验中学2022-2023学年七年级上学期期末数学试题(解析版),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份甘肃省酒泉市第二中学2022-2023学年七年级上学期期末考试数学试题,共4页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。









