

山东省青岛市第二十四中学等2校2022-2023学年九年级下学期开学考试数学试题(无答案)
展开
这是一份山东省青岛市第二十四中学等2校2022-2023学年九年级下学期开学考试数学试题(无答案),共8页。试卷主要包含了选择题,作图题,解答道等内容,欢迎下载使用。
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
本试题共有24道题.其中1-8题为选择题,共24分;9-14题为填空题,共18分;15题为作图题,共4分;16-24题为解答题,共74分.要求所有题目均在答题卡上作答,在本卷上作答无效.
一、选择题(本题满分24分,共有8道小题,每小题3分)
1.如图所示的几何体,它的左视图是( )
A. B.
C. D.
2.如图为最受欢迎的智力游戏之一——三阶魔方,将六个面分别涂有不同颜色的魔方平均分割成27个大小相同的小立方块,从中任取一个小立方块,恰好有两面涂色的概率为( )
A. B. C. D.
3.二次函数在平面直角坐标系中的图象如图所示,则图象与轴的另一个交点的横坐标为( )
A.2 B.3 C.3.5 D.4
4.国家统计局发布报告显示,2019年我国单位GDP能耗约为0.571吨标准煤/万元,而2021年我国单位GDP能耗约为0.555吨标准煤/万元.设平均每年单位GDP能耗降低率为,则可列方程为( )
A. B.
C. D.
5.随着光伏发电项目投资成本下降,越来越多的“光伏+”项目正在逐步走进我们的生活.光伏发电不仅能为城市提供清洁能湆,还能减少城市污染和能源消耗.如图,长宽的太阳能电池板与水平面成夹角,经过太阳光的正投影,它在水平面所形成的阴影的面积为( )
A. B. C. D.
6.如图,的顶点分别在单位长度为1的正方形网格的格点上,则的值为( )
A. B. C. D.
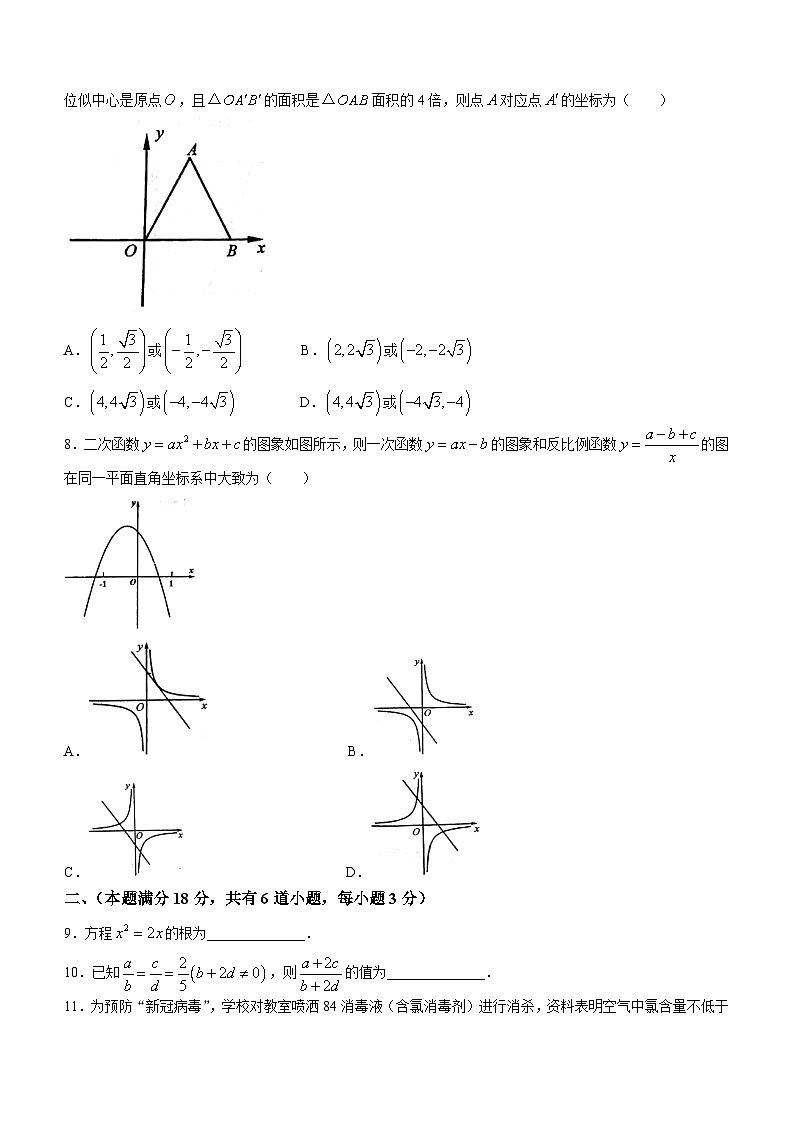
7.如图,在平面直角坐标系中,等边三角形的顶点.已知与位似,位似中心是原点,且的面积是面积的4倍,则点对应点的坐标为( )
A.或 B.或
C.或 D.或
8.二次函数的图象如图所示,则一次函数的图象和反比例函数的图在同一平面直角坐标系中大致为( )
A. B.
C. D.
二、(本题满分18分,共有6道小题,每小题3分)
9.方程的根为______________.
10.已知,则的值为______________.
11.为预防“新冠病毒”,学校对教室喷洒84消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于,才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,与成反比例,则此次消杀的有效作用时间是______________.
12.抛物线向右平移2个单位,再向下平移1个单位得到的函数关系式为______________.
13.关于的一元二次方程有实数根,则的取值范围是______________.
14.如图,在长80米、宽60米的矩形草地上條两条互相垂直的小路,即,,且米,米,则小路的面积为______________米.
三、作图题(本题满分4分)
用圆规、直尺作图,不写作法,但要保留作图痕迹.
15.如图是一块木板下脚料,小明想用这块木板做一个菱形学具;请你帮他在木板上画出以为一个内角且面积最大的菱形.
四、解答道(本题满分74分,共有9道小题)
16.(本题满分8分,每小题4分)
(1)计算:
(2)解方程:
17.(本题满分6分)
中国共产党的助手和后备军——中国共青团,担负着为中国特色社会主义事业培养合格建设者和可靠接班人的根本任务,某校举办了党史宜讲活动庆祝共青团成立一百周年,九年级一班将从报名的5名学生(其中有两名男生,三名女生)中随机抽取两名担任党史宜讲员、请利用树状图或列表法求抽取的2名学生中恰有一名男生和一名女生的概率.
18.(本题满分6分)
某学校为了抓好常态化疫情防控,购进了一批测温仪,如图,测温仪的长,测温距离是,当测温仪与竖直方向的夹角时,测温仪能够测量的最大高度与最小高度的差值是多少?(参考数据:)
19.(本题满分6分)
将一块长方体蛋糕平均分成3份,若按照如图1方式进行分割,每份的蛋糕胚一样多,但奶油不一样多(①和③奶油多,②奶油少),那么如何分割,才能使得3份的蛋糕胚和奶油一样多呢?
如图2,首先我们可以将蛋糕抽象成矩形,用加粗线条表示有奶油的边,然后将矩形沿其对角线分割并拼成如图3的平行四边形,分别取边的三等分点和,如图4,按分割成3份(Ⅰ,Ⅱ,Ⅲ),此种分法能够保证每份的蛋糕胚一样多,奶油是否一样多,我们只需判断每份中加粗线条的长度和是否相等,请你给出判断并加以证明.
20.(本题满分8分)
2022年,中国航天迈着大步向浩瀚宇宙不断探索,这一年,神舟十四号载人飞船成功发射,某航模专卖店向航天爱好者推出了“神舟十四号”飞船模型,每个模型的进价是80元,原计划按每个120元销售,每月能售出30个,经调查发现,这种模型每个降价1元,则每月销售量将增加2个.
(1)直接写出每月销售量(个)与每个降价(元)的函数关系式;
(2)设专卖店销售这种模型每月可获利元,当每个降价多少元时,每月获得的利润最大?最大利润是多少?
21.(本题满分8分)
如图,平行四边形的对角线交于点为中点,过点作交的延长线于,连接与.
(1)求证:;
(2)当四边形是怎样的特殊四边形时,四边形为菱形?请说明理由.
22.(本题满分10分)
如图1,一次函数的图象与轴、轴分别交于和,以为对角线作矩形,点恰好在反比例函数的图象上.
(1)求一次函数和反比例函数的表达式;
(2)如图2,作线段的垂直平分线,交反比例函数图象于点,连接,求的面积;
(3)如图3,若点是轴上一点,则周长的最小值为______________.
23.(本题满分12分)
数学上的对称通常是指轴对称、中心对称,以及对称的思想方法.某数学兴䞢小组进行折纸活动,来感受图形中的对称思想.如图①,将正方形纸片对折后展开,得到折痕;如图②,将纸片再次折叠,便点落在折痕上,记作点;如图③,连接,得到.
(1)请判断:是______________三角形.
【问题提出】
兴趣小组成员想要进一步找到正方形中最大的等边三角形.
【问题探究】
如图④,小颖认为正方形中最大等边三角形的顶点一定落在正方形的边上,她将图④的沿进行平移,使点与点重合(如图⑤),再将绕点旋转,便与对角线垂直,延长分别交于点和(如图⑥),连接,便可得到如图⑦的最大等边三角形.设正方形的边长为2.
(2)小丽利用对称的思想,即关于直线对称,从而求得,则______________.
(3)若不知道角的三角函数值,请你换一种方法求的长.
【问题解决】
(4)如图⑧,已知正六边形中最大的等边三角形边长为4,则该正六边形的边长为______________.
【拓广应用】
(5)A4纸的长为,宽为,现要在A4纸中音一个最大等边三角形.请你在图⑨中画出示意图(不需尺规作图),并求该最大等边三角形的边长.
24.(本题满分10分)
如图,已知抛物线交轴于点(点在点的右侧),交轴于点,其顶点为,连接.
(1)求点的坐标;
(2)求点坐标;
(2)若点为抛物线上一点,且,求点坐标.
相关试卷
这是一份山东省青岛市崂山区2022-2023学年八年级下学期开学考试数学试题(解析版),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份河北省邯郸市丛台区邯郸市育华中学2022-2023学年九年级下学期开学考试数学试题(无答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年山东省济南市稼轩中学九年级下学期开学测试数学试题(无答案),共7页。









