专题5.3 期中复习——选择压轴题专项训练（压轴题专项训练）-2023-2024学年七年级数学上册压轴题专项讲练系列（人教版）

这是一份专题5.3 期中复习——选择压轴题专项训练（压轴题专项训练）-2023-2024学年七年级数学上册压轴题专项讲练系列（人教版），文件包含专题53期中复习选择压轴题专项训练压轴题专项训练人教版原卷版docx、专题53期中复习选择压轴题专项训练压轴题专项训练人教版解析版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

A．1或﹣3B．1或﹣1C．﹣1或3D．3或﹣3
【思路点拨】
根据绝对值的性质及连乘法则，可判断出x、y、z的符号，再根据正负性即可求值.
【解题过程】
解：∵−4xyz|3xyz|=43，
∴xyz<0，
∴x、y、z的符号为三负或两正一负.
当x、y、z均为负值时，
原式＝（－1）+（－1）+（－1）＝－3；
当x、y、z为两正一负时，
原式＝1+1+（－1）＝1；
∴|x|x+y|y|+|z|z值为1或－3.
故选A.
2．（2022秋·辽宁沈阳·七年级统考期中）有理数a、b、c在数轴上对应点的位置如图所示，若|b|＞|c|，则下列结论中正确的是（ ）
A．abc＜0B．b＋c＜0C．a＋c＞0D．ac＞ab
【思路点拨】
根据题意，a和b是负数，但是c的正负不确定，根据有理数加减乘除运算法则讨论式子的正负．
【解题过程】
解：∵b>c，
∴数轴的原点应该在表示b的点和表示c的点的中点的右边，
∴c有可能是正数也有可能是负数，a和b是负数，
ab>0，但是abc的符号不能确定，故A错误；
若b和c都是负数，则b+c<0，若b是负数，c是正数，且b>c，则b+c<0，故B正确；
若a和c都是负数，则a+c<0，若a是正数，c是负数，且a>c，则a+c<0，故C错误；
若b是负数，c是正数，则ac故选：B．
3．（2022秋·浙江绍兴·七年级校联考期中）已知a，b，c为非零有理数，则aa+bb+cc的值不可能为（ ）
A．0B．-3C．-1D．3
【思路点拨】
要对a,b,c所有可能出现的不同情况进行分类讨论，找出符合要求的取值，代入求值．
【解题过程】
解：对a,b,c的取值情况分类讨论如下：
①当a,b,c都是正数时，aa=bb=cc=1，所以和为3；
②当a,b,c都是负数时，aa=bb=cc=-1，所以和为-3；
③当a,b,c中有两个正数，一个负数时，a|a|,b|b|,c|c|中有两个1，一个-1，所以aa+bb+cc=1，
④当a,b,c中有一个正数、两个负数时，a|a|,b|b|,c|c|中有两个-1，一个+1，所以aa+bb+cc=-1，
总之，aa+bb+cc=±1或±3．
故选：A．
4．（2022秋·湖北武汉·七年级校考期中）有理数x、y、z满足x+y+z=x−y−z，且y≠0，则x−y+z+4−y−2的值为（ ）
A．2B．0C．6D．不能求出
【思路点拨】
根据绝对值的意义分情况讨论求解，即可得出结论．
【解题过程】
解：由题意，x−y−z≥0，即x≥y+z，
当x+y+z≥0时，则x+y+z=x+y+z，
∴x+y+z=x−y−z，则y+z=0，
∵y≠0，
∴y=−z≠0，z≠0，
∴x−y+z+4−y−2
=x+z+z+4−−z−2
=x+2z+4−z+2，故其值不能求出；
当x+y+z<0时，则x+y+z=−x−y−z，
∴−x−y−z=x−y−z，则x=0，y+z≤0，
∴x−y+z+4−y−2
=−y+z+4−y−2，故其值不能求出，
故答案为：D．
5．（2022秋·黑龙江大庆·七年级校考期中）已知：m=a+bc+2b+ca+3c+ab，且abc>0，a+b+c=0，则m共有x个不同的值，若在这些不同的m值中，最小的值为y，则x+y=（ ）
A．−1B．1C．2D．3
【思路点拨】
根据题意分析出a、b、c为两个负数，一个正数，分三种情况进行讨论，求出m不同的值，看有多少个，最小的值是多少．
【解题过程】
解：∵abc>0，a+b+c=0，
∴a、b、c为两个负数，一个正数，
∵a+b=−c，b+c=−a，c+a=−b，
∴m=−cc+2−aa+3−bb，
分三种情况讨论，
当a<0，b<0，c>0时，m=1−2−3=−4，
当a<0，c<0，b>0时，m=−1−2+3=0，
当b<0，c<0，a>0时，m=−1+2−3=−2，
∴x=3，y=−4，则x+y=3−4=−1．
故选：A．
6．（2022秋·广东广州·七年级广州大学附属中学校考期中）在数轴上和有理数a、b、c对应的点的位置如图所示，有下列四个结论：
①(a−1)(b−1)(c−1)<0；②a−b+b−c=a−c；③(a+b)(b+c)(c+a)>0；④a<1−bc，其中正确的结论有（ ）个
A．4个B．3个C．2个D．1个
【思路点拨】
根据三点与1的位置关系即可判断①；对于②，根据a、b、c的位置关系化简方程左端，判断是否等于右端即可；对于③，首先判断三个式子的正负，然后判断积的符号；对于④，首先判断1−bc的符号，然后和a比较即可 ．
【解题过程】
解：①∵a<1，b<1，c<1
∴a-1<0，b-1<0，c-1<0
∴(a−1)(b−1)(c−1)<0，故①正确；
②∵a∴a-b<0，b-c<0，a-c<0
∴a−b+b−c=b−a+c−b=c−a，a−c=c−a
∴a−b+b−c=a−c，故②正确；
③∵a+b<0，b+c>0，a+c<0
∴(a+b)(b+c)(c+a)>0，故③正确；
④∵a<-1
∴|a|>1
∵0∴0∴1-bc<1
∴|a|>1-bc，故④错误；
故选B
7．（2022秋·福建福州·七年级校考期中）对于每个正整数n，设fn表示nn+1的末位数字．例如：f1=2（1×2的末位数字），f2=6（2×3的末位数字），f3=2（3×4的末位数字），…则f1+f2+f3+⋅⋅⋅f2021的值为（ ）
A．4042B．4048C．4050D．10
【思路点拨】
试着往下求出几个式子的值，发现结果成一个循环的规律，以2、6、2、0、0为一个循环，用2021除以5得到一共有几组循环，余几，从而求出式子的和．
【解题过程】
解：根据题意，
f4=0（4×5的末位数字），
f5=0（5×6的末位数字），
f6=2（6×7的末位数字），
f7=6（7×8的末位数字），
f8=2（8×9的末位数字），
f9=0（9×10的末位数字），
……
这些数有一个循环的规律，以2、6、2、0、0为一个循环，每组循环的数加起来等于10，
∵2021÷5=404⋯1，
∴原式=404×10+2=4042．
故选：A．
8．（2022秋·广东深圳·七年级校考期中）对于正数x，规定fx=11+x，例如f4=11+4=15,f14=11+14=45，则f(2022)+f2021+f2020+⋯+f2+f1 +f12+⋯+f12020+f12021+f12022的结果是（ ）
A．40432B．4043C．40412D．4041
【思路点拨】
计算出f2，f12，f3，f13的值，总结出其规律，再求所求的式子的值即可．
【解题过程】
解：∵f2=11+2=13，f12=11+12=23，f3=11+3=14，f13=11+13=34，…，
∴f2+f12=13+23=1，f3+f13=14+34=1，…，
∴fx+f1x=1，
∴f2022+f2021+f2020+…+f2+f1+f12+…+f12020+f12021+f12022 =f2022+f12022+f2021+f12021+f2020+f12020+…+f2+f12+f1 =1×2022−1+f1
=2021+12
=40432．
故选：A．
9．（2022秋·湖南娄底·七年级统考期中）规定：fx=x−2，gy=y+3．例如f−4=−4−2，g−4=−4+3．下列结论中：
①若fx+gy=0，则2x−3y=13；
②若x<−3，则fx+gx=−1−2x；
③若x>−3，则fx+gx=2x+1；
④式子fx−1+gx+1的最小值是7．
其中正确的所有结论是（ ）
A．①②B．①②④C．①③④D．①②③④
【思路点拨】
①根据新定义运算和非负数的性质求得x、y，再代值计算便可判断①的正误；
②根据新定义运算和绝对值的性质进行计算便可；
③根据新定义运算和绝对值的性质，分两种情况：−3④根据新定义运算和绝对值的性质，进行解答便可．
【解题过程】
解：①∵fx+gy=0，
∴x−2+y+3=0，
∴x−2=0，y+3=0，
∴x=2，y=−3，
∴2x−3y=4+9=13，
故①正确；
②∵x<−3，
∴fx+gx=x−2+x+3=2−x−x−3=−1−2x，
故②正确；
③∵x>−3，fx+gx=x−2+x+3|
∴当−3当x≥2时，fx+gx=x−2+x+3=x−2+x+3=2x+1，
故③错误；
④fx−1+gx+1=x−1−2+x+1+3=x−3+x+4，
当−4≤x≤33时，式子fx−1+gx+1=x−1−2+x+1+3=x−3+x+4有最小值为：3−x+x+4=7，
故④正确；
故选：B．
10．（2022秋·黑龙江大庆·七年级大庆市第三十六中学校考期中）下列说法中，正确的个数是（ ）
①若1a=1a，则a≥0；②若|a|＞|b|，则有（a+b）（a﹣b）是正数；
③A、B、C三点在数轴上对应的数分别是﹣2、6、x，若相邻两点的距离相等，则x＝2；
④若代数式2x+|9﹣3x|+|1﹣x|+2011的值与x无关，则该代数式值为2021；
⑤a+b+c＝0，abc＜0，则b+c|a|+a+cb+a+b|c|的值为±1．
A．1个B．2个C．3个D．4个
【思路点拨】
根据绝对值的性质，数轴上的两点之间的距离逐项分析即可．
【解题过程】
若1a=1a，则a>0，故①不正确；
∵ a>b，当a>b>0时，
则a+b>0,a−b>0，
∴ a+ba−b>0，
∵ a>b，当a>0>b时，
则a+b>0,a−b>0，
∴ a+ba−b>0
∵ a>b，当a则a+b<0,a−b<0，
∴ a+ba−b>0
∴ a>b，a+ba−b>0，故②正确；
A、B、C三点在数轴上对应的数分别是﹣2、6、x，若相邻两点的距离相等，
当B为AC的中点时，即−2+x2=6，则x=14
当C为AB的中点时，即x=−2+62，则x=2
当A为BC的中点时，即−2=6+x2，则x=−10
故③不正确；
若代数式2x+|9﹣3x|+|1﹣x|+2011的值与x无关，；
即2x+|9﹣3x|+|1﹣x|+2011
=2x+9−3x−1+x+2011
=2019
故④不正确；
∵ abc<0，a+b+c=0
∴ a,b,c有1个负数，2个正数，
设a>0,b>0,c<0，
∵ a+b+c=0，
∴ a=−b+c,b=−a+c,c=−a+b
b+c|a|+a+cb+a+b|c|
=−aa+−bb+−cc=−aa+−bb+−c−c=−1−1+1=−1
故⑤不正确
综上所述，正确的有②，共1个．
故选A．
11．（2022秋·重庆·七年级重庆实验外国语学校校考期中）下列说法正确的有（ ）
①已知a，b，c是非零的有理数，且|abc|abc=−1时，则|a|a+|b|b+|c|c的值为1或−3；
②已知a，b，c是有理数，且a+b+c=0，abc<0时，则b+c|a|+a+c|b|+a+b|c|的值为−1或3；
③已知x≤4时，那么x+3−x−4的最大值为7，最小值为−7；
④若a=b且|a−b|=23，则式子a+b−abb2+1的值为110；
⑤如果定义a,b=a+b(a>b)0a=bb−a(ab时，{a，b}的值为b−a．
A．2个B．3个C．4个D．5个
【思路点拨】
①由题意可得，abc<0，则a，b，c中有一个或三个值为负数，讨论求解即可；②由abc<0可得a，b，c中有一个值为负数，求解即可；③根据x≤4化简绝对值，然后求解即可；④由题意可得a=b或a=−b，分别求解即可；⑤根据题意可得a，b异号，分两种情况求解即可．
【解题过程】
解：①由|abc|abc=−1可得abc<0，a，b，c中有一个或三个值为负数，
当a<0，b>0，c>0时，|a|a+|b|b+|c|c=−1+1+1=1
当a<0，b<0，c<0时，|a|a+|b|b+|c|c=−1−1−1=−3
故①正确；
②由abc<0和a+b+c=0得a，b，c中有一个值为负数，
∴a+b=−c，a+c=−b，b+c=−a
∴−a|a|+−b|b|+−c|c|=1−1−1=−1，
故②错误；
③当−3≤x≤4时，x−4≤0，x+3≥0，
则x+3−x−4=x+3+x−4=2x−1，此时最大值为7，最小值为−7
当x<−3时，x−4≤0，x+3<0
则x+3−x−4=−x−3+x−4=−7
故③正确；
④由a=b可得a=b或a=−b
当a=b时，a−b=0与|a−b|=23矛盾，舍去；
当a=−b时，a−b=−2b，a+b=0且2b=23
解得a=13,b=−13或a=−13,b=13
则ab=−19，b2=19
a+b−abb2+1=1919+1=110
故④正确；
⑤由题意可得a，b异号，
当a<0，b>0时，a=−a，b=b，
由a>b可得−a>b，即a+b<0符合题意，此时a<0则{a，b}=b−a
当a>0，b<0时，a=a，b=−b
由a>b可得a>−b，即a+b>0，与a+b<0矛盾，舍去，
综上{a，b}=b−a
故⑤正确；
正确的个数为4
故选：C．
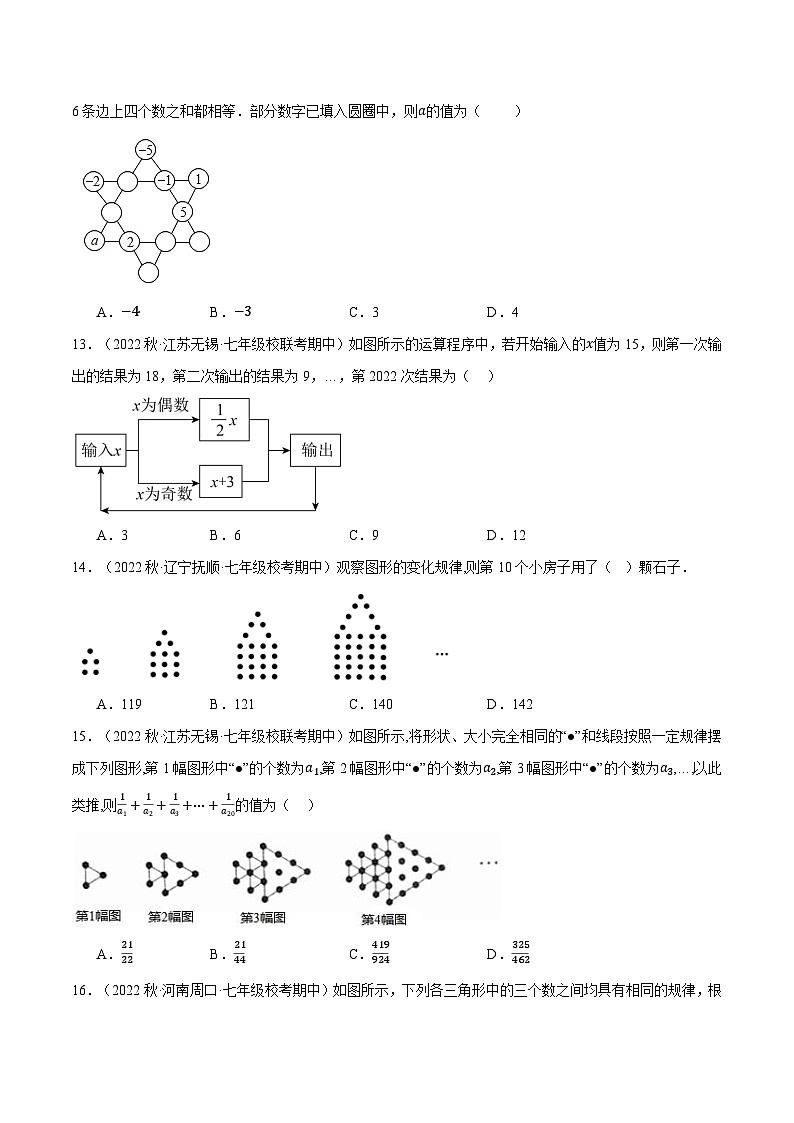
12．（2022秋·浙江温州·七年级校考期中）如图，在探究“幻方”、“幻圆”的活动课上，学生们感悟到我国传统数学文化的魅力．一个小组尝试将数字−5,−4,−3,−2,−1,0,1,2,3,4,5,6这12 个数填入“六角幻星”图中，使6条边上四个数之和都相等．部分数字已填入圆圈中，则a的值为（ ）
A．−4B．−3C．3D．4
【思路点拨】
共有12个数，每一条边上4个数的和都相等，共有六条边，所以每个数都加了两遍，这12
个数共加了两遍后和为12，所以每条边的和为2，然后利用这个原理将剩余的数填入圆圈中，即可得到结果．
【解题过程】
解：因为共有12个数，每一条边上4个数的和都相等，共有六条边，所以每个数都加了两遍，这12个数共加了两遍后和为12，所以每条边的和为2，
所以−5,−1,5这一行最后一个圆圈数字应填3，
则a所在的横着的一行最后一个圈为3，
−2,−1,1这一行第二个圆圈数字应填4，
目前数字就剩下−4,−3,0,6，
1,5这一行剩下的两个圆圈数字和应为−4，则取−4,−3,0,6中的−4,0，
−2,2这一行剩下的两个圆圈数字和应为2，则取−4,−3,0,6中的−4,6，
这两行交汇处是最下面那个圆圈，应填−4，
所以1,5这一行第三个圆圈数字应为0，
则a所在的横行，剩余3个圆圈里分别为2,0,3，要使和为2，则a为−3
故选：B
13．（2022秋·江苏无锡·七年级校联考期中）如图所示的运算程序中，若开始输入的x值为15，则第一次输出的结果为18，第二次输出的结果为9，…，第2022次结果为（ ）
A．3B．6C．9D．12
【思路点拨】
根据运算程序先判断输入的数是奇数还是偶数，是奇数选择x+3运算，是偶数选择12x计算，直到从第4次开始偶数次输出结果为6，奇数次输出结果为3，根据2022为偶数，即可得出第2022次结果．
【解题过程】
解：第1次输入的x值为15，奇数，x+3=18，
第2次输入的x值为18，偶数，12x=12×18=9，
第3三次输入的x值为9，奇数，x+3=9+3=12，
第4次输入的x值为12，偶数，12x=12×12=6，
第5次输入的x值为6，偶数，12x=12×6=3，
第6次输入的x值为3，奇数，x+3=3+3=6，
第7次输入的x值为6，偶数，12x=12×6=3，
第8次输入的x值为3，偶数，x+3=3+3=6，
…
从第4次开始偶数次输出结果为6，奇数次输出结果为3，
∵2022为偶数，
∴第2022次结果为6．
故选择B．
14．（2022秋·辽宁抚顺·七年级校考期中）观察图形的变化规律,则第10个小房子用了（ ）颗石子．
A．119B．121C．140D．142
【思路点拨】
根据前4个图形归纳类推出一般规律，由此即可得．
【解题过程】
解：第1个小房子所用石子的颗数为5=22+1=(1+1)2+2×1−1，
第2个小房子所用石子的颗数为12=32+3=(2+1)2+2×2−1，
第3个小房子所用石子的颗数为21=42+5=(3+1)2+2×3−1，
第4个小房子所用石子的颗数为32=52+7=(4+1)2+2×4−1，
归纳类推得：第n个小房子所用石子的颗数为(n+1)2+2n−1，其中n为正整数，
则第10个小房子所用石子的颗数为(10+1)2+2×10−1=140，
故选：C．
15．（2022秋·江苏无锡·七年级校联考期中）如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1,第2幅图形中“●”的个数为a2,第3幅图形中“●”的个数为a3,…,以此类推,则1a1+1a2+1a3+⋯+1a20的值为（ ）
A．2122B．2144C．419924D．325462
【思路点拨】
图中的黑点数有如下规律：a1=3=1×3，a2=8=2×4，a3=15=3×5，以此类推，an=n×(n+2)，则1a1+1a2+1a3+⋯+1a20=11×3+12×4+13×5+⋯+120×22=12(1−13+12−14+13−15+⋯+120−122)，计算即可得出结论.
【解题过程】
解：根据题意，图中的黑点数有如下规律：a1=3=1×3，a2=8=2×4，a3=15=3×5，以此类推，an=n×(n+2)，
∴1a1+1a2+1a3+⋯+1a20=11×3+12×4+13×5+⋯+120×22，
=12(1−13+12−14+13−15+⋯+120−122)，
=12(1+12−121−122)，
=325462，
故答案为D.
16．（2022秋·河南周口·七年级校考期中）如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，则第n（n为正整数）个三角形中，用n表示y的式子为（ ）

A．2n+1B．2n+nC．2n+1+nD．2n+n+1
【思路点拨】
由题意可得各三角形中下边第三个数是上边两个数字的和，而上边第一个数的数字规律为1，2，3，…，n，第二个数的数字规律为：2，22，23，…，2n，由此即可得到答案．
【解题过程】
解：由题意可得：
三角形上边第一个数的数字规律为：1，2，3，…，n，
三角形上边第二个数的数字规律为：2，22，23，…，2n，
三角形下边的数的数字规律为： 1+2=1+21=3，2+4=2+22=6，3+8=3+23=11，…，
∴第n个三角形中的数的规律为：y=n+2n，
故选：B．
17．（2022秋·浙江温州·七年级校联考期中）正整数按如图的规律排列，则2022位于哪一行，哪一列（ ）
A．第45行 第4列B．第4行 第45列
C．第46行 第3列D．第3行 第46列
【思路点拨】
观察图形可知这些数字排成的是一个正方形，则由44×44=1936，45×45=2025，即可判断2022的位置．
【解题过程】
解：观察图形可知这些数字排成的是一个正方形，
∵44×44=1936＜2022＜45×45=2025，
∴2022在第45列，
∵2025−2022=3，
∴2022在第4行，即2022位于第4行，第45列．
故选：B．
18．（2022秋·湖北荆门·七年级校考期中）我国宋朝时期的数学家杨辉，曾将大小完全相同的圆弹珠逐层堆积，形成“三角垛”，图1有1颗弹珠；图2有3颗弹珠；图3有6颗弹珠，往下依次是第4个图，第5个图，…；如图中画出了最上面的四层．若用an表示图n的弹珠数，其中n=1，2，3，…，则1a1+1a2+1a3+⋯+1a2022=（ ）

A．40442023B．20212023C．20211011D．40422023
【思路点拨】
可找出规律：a2022=1+2+3+4+⋯+2022=20221+20222=2022×20232，从而可将1a1+1a2+1a3+⋯+1a2022化为21×2+22×3+23×4+24×5+⋯+22022×2023，对其进行裂项运算，即可求解．
【解题过程】
解：当n=1时，a1=1=1×22，
当n=2时，a2=1+2=21+22=2×32，
当n=3时，a3=1+2+3=31+32=3×42，
当n=4时，a4=1+2+3+4=41+42=4×52，
…
第n个图：a2022=1+2+3+4+⋯+2022=20221+20222=2022×20232；
1a1+1a2+1a3+⋯+1a2022
=21×2+22×3+23×4+24×5+⋯+22022×2023
=211×2+12×3+13×4+14×5+⋯+12022×2023
=21−12+12−13+13−14+14−15+⋯+12022−12023
=21−12023
=40442023；
故选：A．
19．（2022秋·浙江宁波·七年级校考期中）取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得1，这个结论在数学上还没有得到证明，但举例验证都是正确的．例如：取自然数5，经过下面5步运算可得1，即：如图所示，如果自然数m恰好经过6步运算可得到1，则所有符合条件的m的值有( )
A．1 个B．2 个C．3 个D．4 个
【思路点拨】
首先根据题意，应用逆推法，用1乘以2，得到2；用2乘以2，得到4；用4乘以2，得到8；用8乘以2，得到16；然后分类讨论，判断出所有符合条件的m的值为多少即可．
【解题过程】
解：根据分析，可得
则所有符合条件的m的值为：64、10．共2个，
故选：B．
20．（2022秋·广东深圳·七年级校考期中）我们把11−a称为有理数aa≠1的差倒数，如：2的差倒数是11−2=−1，-2的差倒数是11−−2=13．如果a1=−3，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，依此类推，那么a1−a2+a3−a4+⋯+a2017−a2018+a2019−a2020的值是（ ）
A．−134B．−3C．114D．1312
【思路点拨】
根据“差倒数”的定义，写出前几个数，从而可以发现数字的变化规律，然后即可求得所求式子的值．
【解题过程】
解：由题意可得，
a1=−3，
a2=11−(−3)=14，
a3=11−14=43，
a4=11−43=−3，
…，
则a1，a2，a3，…，这列数每三个数一个循环．
∵2020÷6=336……4，
∴a1−a2+a3−a4+……+a2017−a2018+a2019−a2020
=(a1−a2+a3)−(a4−a5+a6)+……+(a2011−a2012+a2013)−(a2014−a2015+a2016)+(a2017−a2018+a2019)−a2020 =0−0+…+(a2017−a2018+a2019)−a2020
=(−3−14+43)−(−3)
=1312．
故选：D．
21．（2022秋·浙江·七年级期中）如图，大长方形ABCD是由一张周长为C1正方形纸片①和四张周长分别为C2，C3，C4，C5的长方形纸片②，③，④，⑤拼成，若大长方形周长为定值，则下列各式中为定值的是（ ）
A．C1B．C3+C5C．C1+C3+C5D．C1+C2+C4
【思路点拨】
将各长方形的边长标记出来，可将大长方形ABCD的周长为C和正方形纸片①的周长C1和四张长方形纸片②，③，④，⑤的周长分别为C2，C3，C4，C5表示出来，其中大长方形ABCD的周长为C为定值，然后分别计算C3+C5，C1+C3+C5，C1+C2+C4，找出其中为定值的即可．
【解题过程】
解：如图，将各长方形的边长标记出来，
∴大长方形ABCD的周长为C=2a+2b+2c+2ℎ为定值，
∴C2=2a+2b，C3=2c+2d，C4=2e+2f，C5=2ℎ+2g，
∵①是正方形，
∴c−f=e−ℎ=g−b=a−d
∴a+b=g+d，
∴C3+C5=2c+2d+2ℎ+2g=2a+2b+2c+2ℎ=C，
C1+C3+C5=4a−d+2c+2d+2ℎ+2g=4a−2d+2c+2ℎ+2g，
C1+C2+C4=4a−d+2a+2b+2e+2f=6a−4d+2b+2e+2f，
∴C3+C5为定值，
故选：B．
22．（2022秋·河北承德·七年级统考期中）如图，在数轴上，点A表示1，现将点A沿数轴做如下移动，第一次点A向左移动3个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种规律下去，第n次移动到点An，如果点An，与原点的距离不少于20，那么n的最小值是（ ）
A．11B．12C．13D．20
【思路点拨】
当n为奇数的点在点A的左边，各点所表示的数依次减少3，当n为偶数的点在点A的右侧，各点所表示的数依次增加3．
【解题过程】
解：根据题目已知条件，A1表示的数，1﹣3=﹣2；A2表示的数为﹣2+6=4；A3表示的数为4﹣9=﹣5；A4表示的数为﹣5+12=7；A5表示的数为7﹣15=﹣8；A6表示的数为7+3=10，A7表示的数为﹣8﹣3=﹣11，A8表示的数为10+3=13，A9表示的数为﹣11﹣3=﹣14，A10表示的数为13+3=16，A11表示的数为﹣14﹣3=﹣17，A12表示的数为16+3=19，A13表示的数为﹣17﹣3=﹣20．
所以点An与原点的距离不小于20，那么n的最小值是13．
故选C．
23．（2022秋·江苏徐州·七年级统考期中）正方形ABCD在数轴上的位置如图所示，点A、B对应的数分别为−2和−1，若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点C所对应的数为0；则翻转2022次后，点C所对应的数是（ ）
A．2020B．2021C．2022D．2023
【思路点拨】
通过前面几次的分析、归纳，发现每4次一个循环，点C所对应的数有规律地变化；翻转4n−3(n为正整数）次后，点C所对应的数为4(n−1)；翻转4n−2次后，点C所对应的数为4(n−1)；翻转4n−1次后，点C所对应的数为4n−3；翻转4n次后，点C所对应的数为4n−1；于是令2022=4n−2即可得解．
【解题过程】
解：翻转1次后，点C所对应的数为0；
翻转2次后，点C所对应的数为0；
翻转3次后，点C所对应的数为1；
翻转4次后，点C所对应的数为3；
翻转5次后，点C所对应的数为4；
翻转6次后，点C所对应的数为4；
翻转7次后，点C所对应的数为5；
翻转8次后，点C所对应的数为7；
翻转9次后，点C所对应的数为8；
……
翻转4n−3次后，点C所对应的数为4(n−1)；
翻转4n−2次后，点C所对应的数为4(n−1)；
翻转4n−1次后，点C所对应的数为4n−3；
翻转4n次后，点C所对应的数为4n−1；
∵2022÷4=505余2，
∴令2022=4n−2，
∴n=506，
∴4(n−1)=4×505=2020
∴翻转2022次后，点C所对应的数为2020；
故选：A．
24．（2022秋·重庆梁平·七年级校联考期中）如图，在数轴上，点P表示−1，将点P沿数轴做如下移动，第一次点P向右平移2个单位长度到达点P1，第二次将点P1向左移动4个单位长度到达P2，第三次将点P2向右移动6个单位长度，按照这种移动规律移动下去，第n次移动到点Pn，给出以下结论：①P5表示5；②P12>P11；③若点Pn到原点的距离为15，则n=15； ④当n为奇数时，Pn−Pn−1=2Pn；以上结论正确的是（ ）

A．①②③B．①②④C．②③D．①④
【思路点拨】
先根据数轴的定义分别求出点P1,P2,P3,P4,P5,P6表示的数，再归纳类推出一般规律，然后逐个判断即可得．
【解题过程】
解：由题意，点P1表示的数为−1+2=1，
点P2表示的数为1−4=−3，
点P3表示的数为−3+6=3，
点P4表示的数为3−8=−5，
点P5表示的数为−5+10=5，
点P6表示的数为5−12=−7，
归纳类推得：当n为奇数时，Pn=n；当n为偶数时，Pn=−1n+1n+1，其中n为正整数，
则P5表示的数为5，结论①正确；
∵P11=11，P12=−112+1×12+1=−13，
∴P12当n为奇数时，Pn=n=15，
当n为偶数时，Pn=−1n+1n+1=n+1=15，解得n=14，
即若点Pn到原点的距离为15，则n=14或n=15，结论③错误；
当n为奇数时，Pn−Pn−1=n−−1n−1+1n−1+1，
=n−−1nn，
=n−−1n，
=n+n，
=2n，
=2Pn，
即当n为奇数时，Pn−Pn−1=2Pn，结论④正确；
综上，结论正确的是①④，
故选：D．
25．（2022秋·福建厦门·七年级福建省厦门第六中学校考期中）七年级某班的学生共有49人，军训时排列成7×7的方阵，做了一个游戏，起初全体学生站立，教官每次任意点n个不同学号的学生，被点到的学生，站立的蹲下，蹲下的站立，且学生都正确完成指令同一名学生可以多次被点，则m次点名后，（n，m为正整数）下列说法正确的是（ ）
A．当n为偶数时，无论m何值，蹲下的学生人数不可能为奇数个
B．当n为偶数时，无论m何值，对下的学生人数不可能为偶数个
C．当n为奇数时，无论m何值，蹲下的学生人数不可能为偶数个
D．当n为奇数时，无论m何值，蹲下的学生人数不可能为奇数个
【思路点拨】
假设站立记为“+1”，则蹲下为“−1”，开始时49个“+1”，其乘积为“+1”，每次改变其中的n个数，当n为偶数时，每次的改变其中n个数，都不改变上一次的符号，则m次点名后，乘积仍然是“+1”，故最后出现的“−1”的个数为偶数，即蹲下的人数为偶数；即可获解．
【解题过程】
解：假设站立记为“+1”，则蹲下为“−1”，开始时49个“+1”，其乘积为“+1”．
∵每次改变其中的n个数，经过m次点名，
①当n为偶数时，
若有偶数个“+1”偶数个“−1”，变为偶数个“−1”偶数个“+1”，其积的符号不变；
若有奇数个“+1”奇数个“−1”，变为奇数个“−1”奇数个“+1”，其积的符号不变；
故当n为偶数时，每次改变其中的n个数，其积的符号不变，那么m次点名后，乘积仍然是“+1”，
故最后出现的“−1”的个数为偶数，即蹲下的人数为偶数；
②当n为奇数时，
若有偶数个“+1”奇数个“−1”，变为偶数个“−1”奇数个“+1”，其积的符号改变；
若有奇数个“+1”偶数个“−1”，变为奇数个“−1”偶数个“+1”，其积的符号改变；
故当n为奇数时，每次改变其中的n个数，其积的符号改变，
那么m次点名后，
若m为偶数，乘积仍然是“+1”，故最后出现的“−1”的个数为偶数，即蹲下的人数为偶数；
若m为奇数，乘积最后是“−1”，故最后出现的“−1”的个数为奇数，即蹲下的人数为奇数；
综上所述，选项A正确，选项B、C、D均错误；
故选：A．
26．（2022秋·重庆沙坪坝·七年级重庆南开中学校考期中）有依次排列的两个整式：x，x−2，对任意相邻的两个整式，都用左边的整式减去右边的整式，所得的差写在这两个整式之间，可以产生一个新的整式串：x，2，x−2，这称为第一次操作；将第一次操作后的整式串按上述方式再做一次操作，可以得到第二次操作后的整式串：x，x−2，2，4−x，x−2，以此类推．通过实际操作，小南同学得到以下结论：①第二次操作后，当x<2时，所有整式的积为正数；②第三次操作后整式串共有9个整式；③第n次操作后整式串共有2n+1个整式（n为正整数）；④第2023次操作后，所有的整式的和为2x+4044．四个结论正确的有（ ）
A．1个B．2个C．3个D．4个
【思路点拨】
①根据第二次操作后，当x<2时，各个整式的正负，判断所有整式的积的正负：②根据第三次操作后整式的个数判定；③根据前四次操作结果，探究每次操作整式个数与操作次数关系的规律判定；④根据前四次操作结果，探究每次操作所有整式的和与操作次数关系的规律解答
【解题过程】
解：①原整式为：x，x−2，
第1次操作后所得整式串为：x，2，x−2，
第2次操作后所得整式串为：x，x−2，2，4−x，x−2，
此次所有整式之积为，2xx−224−x，
∵x<2，
∴当−20，4−x>0，
∴2xx−224−x≤0，①不正确；
②第3次操作后所得整式串为：x，2，x−2，x−4，2，x−2，4−x，6−2x，x−2，共有9个整式，②正确；
③第1次操作后整式串共有3个整式，3=2+1，
第2次操作后整式串共有5个整式5=22+1，，
第3次操作后整式串共有9个整式，9=23+1，
第4次操作后整式串共有17个整式，17=24+1，
……，
第n次操作后整式串共有整式个数为：2n+1，③正确；
④第1次操作后所得整式串为：x，2，x−2，所有整式之和为：2x，
第2次操作后所得整式串为：x，x−2，2，4−x，x−2，所有整式之和为：2x+2，
第3次操作后所得整式串为：x，2，x−2，x−4，2，x−2，4−x，6−2x，x−2，所有整式之和为：2x+4，
第4次操作后所得整式串为：x，x−2，2，4−x，x−2，2，x−4，x−6，2，4−x，x−2，2x−6，4−x，x−2，6−2x，8−3x，x−2，所有整式之和为：2x+6，
……，
第n次操作后所得所有整式的和为：2x+2n−1，
故操作第2023次操作后所有整式之和为：2x+2×2013−1=2x+4044．④正确．
故选：C．