



专题21 图形的相似(共29题)-2023年全国各地中考数学真题分项汇编(全国通用)
展开一、单选题
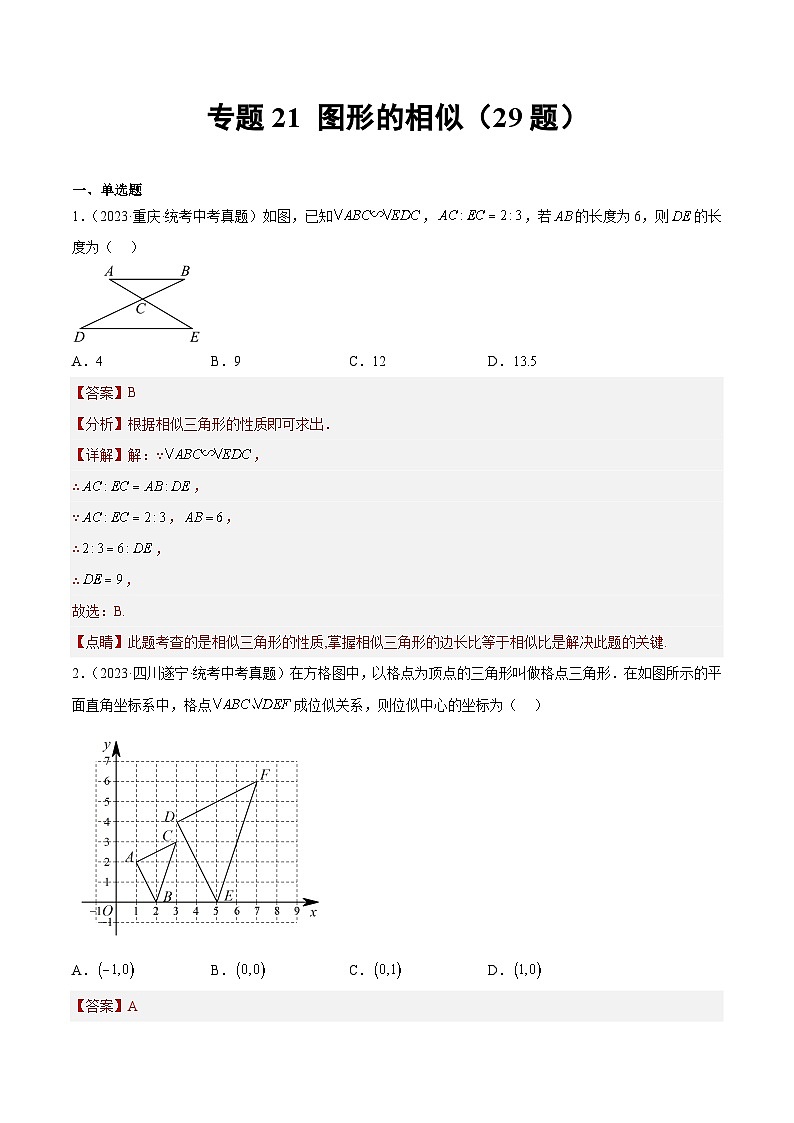
1.(2023·重庆·统考中考真题)如图,已知,,若的长度为6,则的长度为( )
A.4B.9C.12D.
【答案】B
【分析】根据相似三角形的性质即可求出.
【详解】解:∵,
∴,
∵,,
∴,
∴,
故选:B.
【点睛】此题考查的是相似三角形的性质,掌握相似三角形的边长比等于相似比是解决此题的关键.
2.(2023·四川遂宁·统考中考真题)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点成位似关系,则位似中心的坐标为( )
A.B.C.D.
【答案】A
【分析】根据题意确定直线的解析式为:,由位似图形的性质得出所在直线与BE所在直线x轴的交点坐标即为位似中心,即可求解.
【详解】解:由图得:,
设直线的解析式为:,将点代入得:
,解得:,
∴直线的解析式为:,
所在直线与BE所在直线x轴的交点坐标即为位似中心,
∴当时,,
∴位似中心的坐标为,
故选:A.
【点睛】题目主要考查位似图形的性质,求一次函数的解析式,理解题意,掌握位似图形的特点是解题关键.
3.(2023·浙江嘉兴·统考中考真题)如图,在直角坐标系中,的三个顶点分别为,现以原点O为位似中心,在第一象限内作与的位似比为2的位似图形,则顶点的坐标是( )
A.B.C.D.
【答案】C
【分析】直接根据位似图形的性质即可得.
【详解】解:∵的位似比为2的位似图形是,且,
,即,
故选:C.
【点睛】本题考查了坐标与位似图形,熟练掌握位似图形的性质是解题关键.
4.(2023·四川南充·统考中考真题)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为( )
A.B.C.D.
【答案】B
【分析】根据镜面反射性质,可求出,再利用垂直求,最后根据三角形相似的性质,即可求出答案.
【详解】解:如图所示,
由图可知,,,
.
根据镜面的反射性质,
∴,
∴,
,
,
.
小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,
,,.
.
.
故选:B.
【点睛】本题考查了相似三角形的应用,解题的关键在于熟练掌握镜面反射的基本性质和相似三角形的性质.
5.(2023·安徽·统考中考真题)如图,点在正方形的对角线上,于点,连接并延长,交边于点,交边的延长线于点.若,,则( )
A.B.C.D.
【答案】B
【分析】根据平行线分线段成比例得出,根据,得出,则,进而可得,根据,得出,根据相似三角形的性质得出,进而在中,勾股定理即可求解.
【详解】解:∵四边形是正方形,,,
∴,,,
∵,
∴
∴,,
∴,
则,
∴,
∵,
∴,
∴
∴,
在中,,
故选:B.
【点睛】本题考查了正方形的性质,平行线分线段成比例,相似三角形的性质与判定,勾股定理,熟练掌握以上知识是解题的关键.
6.(2023·湖北黄冈·统考中考真题)如图,矩形中,,以点B为圆心,适当长为半径画弧,分别交,于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线,过点C作的垂线分别交于点M,N,则的长为( )
A.B.C.D.4
【答案】A
【分析】由作图可知平分,设与交于点O,与交于点R,作于点Q,根据角平分线的性质可知,进而证明,推出,设,则,解求出.利用三角形面积法求出,再证,根据相似三角形对应边成比例即可求出.
【详解】解:如图,设与交于点O,与交于点R,作于点Q,
矩形中,,
,
.
由作图过程可知,平分,
四边形是矩形,
,
又,
,
在和中,
,
,
,
,
设,则,
在中,由勾股定理得,
即,
解得,
.
.
,
.
,,
,
,即,
解得.
故选:A.
【点睛】本题考查角平分线的作图方法,矩形的性质,角平分线的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等,涉及知识点较多,有一定难度,解题的关键是根据作图过程判断出平分,通过勾股定理解直角三角形求出.
7.(2023·四川内江·统考中考真题)如图,在中,点D、E为边的三等分点,点F、G在边上,,点H为与的交点.若,则的长为( )
A.1B.C.2D.3
【答案】C
【分析】由三等分点的定义与平行线的性质得出,,,是的中位线,易证,得,解得,则.
【详解】解:、为边的三等分点,,
,,,
,是的中位线,
,
,
,
,即,
解得:,
,
故选:C.
【点睛】本题考查了三等分点的定义、平行线的性质、相似三角形的判定与性质、三角形中位线定理等知识;熟练掌握相似三角形的判定与性质是解题的关键.
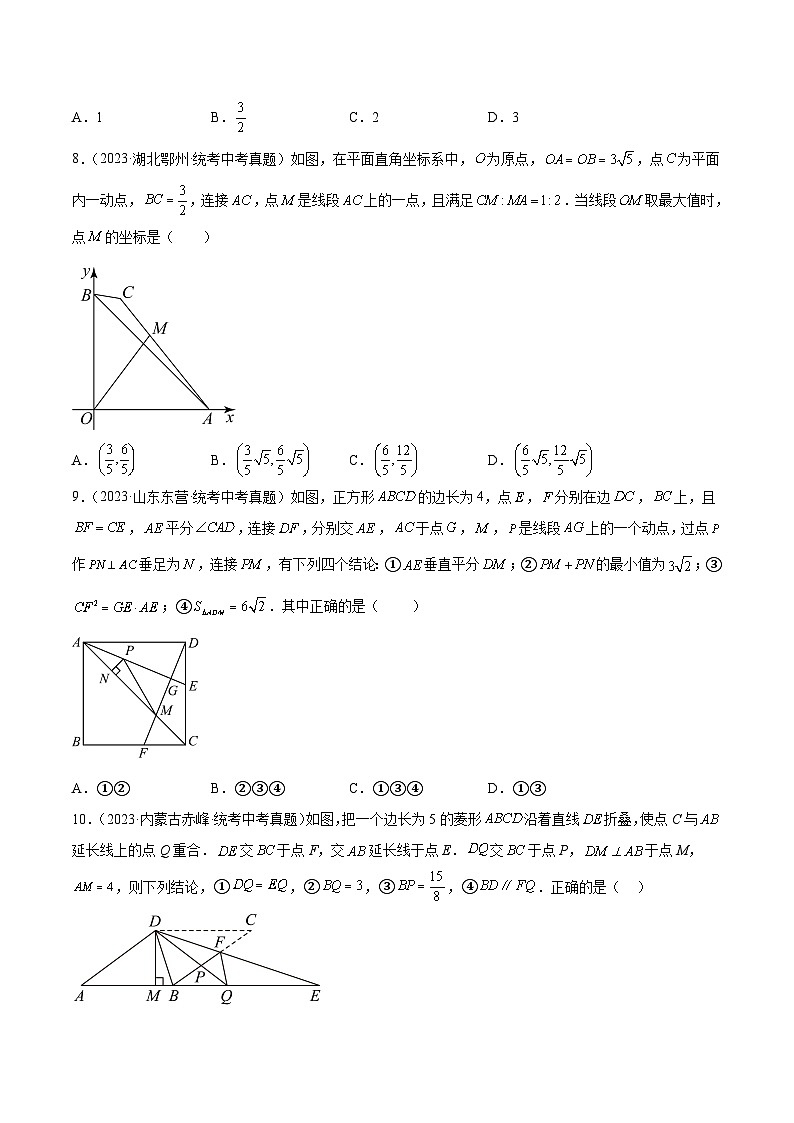
8.(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,为原点,,点为平面内一动点,,连接,点是线段上的一点,且满足.当线段取最大值时,点的坐标是( )
A.B.C.D.
【答案】D
【分析】由题意可得点在以点为圆心,为半径的上,在轴的负半轴上取点,连接,分别过、作,,垂足为、,先证,得,从而当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,然后分别证,,利用相似三角形的性质即可求解.
【详解】解:∵点为平面内一动点,,
∴点在以点为圆心,为半径的上,
在轴的负半轴上取点,连接,分别过、作,,垂足为、,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,
∵,,
∴,
∴,
∵,
∴,
∵轴轴,,
∴,
∵,
∴,
∴即,
解得,
同理可得,,
∴即,
解得,
∴,
∴当线段取最大值时,点的坐标是,
故选:D.
【点睛】本题主要考查了勾股定理、相似三角形的判定及性质、圆的一般概念以及坐标与图形,熟练掌握相似三角形的判定及性质是解题的关键.
9.(2023·山东东营·统考中考真题)如图,正方形的边长为4,点,分别在边,上,且,平分,连接,分别交,于点,,是线段上的一个动点,过点作垂足为,连接,有下列四个结论:①垂直平分;②的最小值为;③;④.其中正确的是( )
A.①②B.②③④C.①③④D.①③
【答案】D
【分析】根据正方形的性质和三角形全等即可证明,通过等量转化即可求证,利用角平分线的性质和公共边即可证明,从而推出①的结论;利用①中的部分结果可证明推出,通过等量代换可推出③的结论;利用①中的部分结果和勾股定理推出和长度,最后通过面积法即可求证④的结论不对;结合①中的结论和③的结论可求出的最小值,从而证明②不对.
【详解】解: 为正方形,
,,
,
,
.
,
,
,
,
.
平分,
.
,
.
,
,
垂直平分,
故①正确.
由①可知,,,
,
,
,
由①可知,
.
故③正确.
为正方形,且边长为4,
,
在中,.
由①可知,,
,
.
由图可知,和等高,设高为,
,
,
,
.
故④不正确.
由①可知,,
,
关于线段的对称点为,过点作,交于,交于,
最小即为,如图所示,
由④可知的高即为图中的,
.
故②不正确.
综上所述,正确的是①③.
故选:D.
【点睛】本题考查的是正方形的综合题,涉及到三角形相似,最短路径,三角形全等,三角形面积法,解题的关键在于是否能正确找出最短路径以及运用相关知识点.
10.(2023·内蒙古赤峰·统考中考真题)如图,把一个边长为5的菱形沿着直线折叠,使点C与延长线上的点Q重合.交于点F,交延长线于点E.交于点P,于点M,,则下列结论,①,②,③,④.正确的是( )
A.①②③B.②④C.①③④D.①②③④
【答案】A
【分析】由折叠性质和平行线的性质可得,根据等角对等边即可判断①正确;根据等腰三角形三线合一的性质求出,再求出即可判断②正确;由得,求出即可判断③正确;根据即可判断④错误.
【详解】由折叠性质可知:,
∵,
∴.
∴.
∴.
故正确;
∵,,
∴.
∵,
∴.
故正确;
∵,
∴.
∴.
∵,
∴.
故正确;
∵,
∴.
∴.
∴.
∵,
∴.
∴与不相似.
∴.
∴与不平行.
故错误;
故选:A.
【点睛】本题主要考查了折叠的性质,平行线的性质,等腰三角形的性质,相似三角形的判定和性质,菱形的性质等知识,属于选择压轴题,有一定难度,熟练掌握相关性质是解题的关键.
11.(2023·黑龙江·统考中考真题)如图,在正方形中,点分别是上的动点,且,垂足为,将沿翻折,得到交于点,对角线交于点,连接,下列结论正确的是:①;②;③若,则四边形是菱形;④当点运动到的中点,;⑤.( )
A.①②③④⑤B.①②③⑤C.①②③D.①②⑤
【答案】B
【分析】利用正方形的性质和翻折的性质,逐一判断,即可解答.
【详解】解:四边形是正方形,
,,
,
,
,
,
,
,故①正确,
将沿翻折,得到,
,
∵,
,故②正确,
当时,,
,
,即在同一直线上,
,
,
通过翻折的性质可得,,
∴,,
,
四边形是平行四边形,
,
平行四边形是菱形,故③正确,
当点运动到的中点,如图,
设正方形的边长为,则,
在中,,
,
,
,
,
,
,
,
,,
,,
,
在中,,故④错误,
,
,
,,
,
根据翻折的性质可得,
,
,
,故⑤正确;
综上分析可知,正确的是①②③⑤.
故选:B.
【点睛】本题考查了正方形的性质,翻折的性质,相似三角形的判定和性质,正切的概念,熟练按照要求做出图形,利用寻找相似三角形是解题的关键.
二、填空题
12.(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,与位似,原点O是位似中心,且.若,则点的坐标是___________.
【答案】
【分析】直接利用位似图形的性质得出相似比进而得出对应线段的长.
【详解】解∶设
∵与位似,原点是位似中心,且.若,
∴位似比为,
∴,
解得,,
∴
故答案为:.
【点睛】此题主要考查了位似变换,正确得出相似比是解题关键.
13.(2023·吉林长春·统考中考真题)如图,和是以点为位似中心的位似图形,点在线段上.若,则和的周长之比为__________.
【答案】
【分析】根据位似图形的性质即可求出答案.
【详解】解:,
,
设周长为,设周长为,
和是以点为位似中心的位似图形,
.
.
和的周长之比为.
故答案为:.
【点睛】本题考查了位似图形的性质,解题的关键在于熟练掌握位似图形性质.
14.(2023·四川乐山·统考中考真题)如图,在平行四边形中,E是线段上一点,连结交于点F.若,则__________.
【答案】
【分析】四边形是平行四边形,则,可证明,得到,由进一步即可得到答案.
【详解】解:∵四边形是平行四边形,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
故答案为:
【点睛】此题考查了平行四边形的性质、相似三角形的判定和性质等知识,证明是解题的关键.
15.(2023·江西·统考中考真题)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点,,在同一水平线上,和均为直角,与相交于点.测得,则树高______m.
【答案】
【分析】根据题意可得,然后相似三角形的性质,即可求解.
【详解】解:∵和均为直角
∴,
∴,
∴
∵,
∴,
故答案为:.
【点睛】本题考查了相似三角形的应用,熟练掌握相似三角形的性质与判定是解题的关键.
16.(2023·四川成都·统考中考真题)如图,在中,是边上一点,按以下步骤作图:①以点为圆心,以适当长为半径作弧,分别交,于点,;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点:④过点作射线交于点.若与四边形的面积比为,则的值为___________.
【答案】
【分析】根据作图可得,然后得出,可证明,进而根据相似三角形的性质即可求解.
【详解】解:根据作图可得,
∴,
∴,
∵与四边形的面积比为,
∴
∴
∴,
故答案为:.
【点睛】本题考查了作一个角等于已知角,相似三角形的性质与判定,熟练掌握基本作图与相似三角形的性质与判定是解题的关键.
17.(2023·内蒙古·统考中考真题)如图,在中,,将绕点A逆时针方向旋转,得到.连接,交于点D,则的值为________.
【答案】5
【分析】过点D作于点F,利用勾股定理求得,根据旋转的性质可证、是等腰直角三角形,可得,再由,得,证明,可得,即,再由,求得,从而求得,,即可求解.
【详解】解:过点D作于点F,
∵,,,
∴,
∵将绕点A逆时针方向旋转得到,
∴,,
∴是等腰直角三角形,
∴,
又∵,
∴,
∴是等腰直角三角形,
∴,
∵,即,
∵ ,,
∴,
∴,即,
又∵,
∴,
∴,,
∴,
故答案为:5.
【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,熟练掌握相关知识是解题的关键.
18.(2023·河南·统考中考真题)矩形中,M为对角线的中点,点N在边上,且.当以点D,M,N为顶点的三角形是直角三角形时,的长为______.
【答案】2或
【分析】分两种情况:当时和当时,分别进行讨论求解即可.
【详解】解:当时,
∵四边形矩形,
∴,则,
由平行线分线段成比例可得:,
又∵M为对角线的中点,
∴,
∴,
即:,
∴,
当时,
∵M为对角线的中点,
∴为的垂直平分线,
∴,
∵四边形矩形,
∴,则,
∴
∴,
综上,的长为2或,
故答案为:2或.
【点睛】本题考查矩形的性质,平行线分线段成比例,垂直平分线的判定及性质等,画出草图进行分类讨论是解决问题的关键.
19.(2023·辽宁大连·统考中考真题)如图,在正方形中,,延长至,使,连接,平分交于,连接,则的长为_______________.
【答案】
【分析】如图,过作于,于,由平分,可知,可得四边形是正方形,,设,则,证明,则,即,解得,,由勾股定理得,计算求解即可.
【详解】解:如图,过作于,于,则四边形是矩形,,
∵平分,
∴,
∴,
∴四边形是正方形,
设,则,
∵,
∴,
∴,即,解得,
∴,
由勾股定理得,
故答案为:.
【点睛】本题考查了正方形的判定与性质,勾股定理,相似三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.
20.(2023·广东·统考中考真题)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为_______.
【答案】15
【分析】根据正方形的性质及相似三角形的性质可进行求解.
【详解】解:如图,
由题意可知,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
故答案为:15.
【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.
21.(2023·天津·统考中考真题)如图,在边长为3的正方形的外侧,作等腰三角形,.
(1)的面积为________;
(2)若F为的中点,连接并延长,与相交于点G,则的长为________.
【答案】3;
【分析】(1)过点E作,根据正方形和等腰三角形的性质,得到的长,再利用勾股定理,求出的长,即可得到的面积;
(2)延长交于点K,利用正方形和平行线的性质,证明,得到的长,进而得到的长,再证明,得到,进而求出的长,最后利用勾股定理,即可求出的长.
【详解】解:(1)过点E作,
正方形的边长为3,
,
是等腰三角形,,,
,
在中,,
,
故答案为:3;
(2)延长交于点K,
正方形的边长为3,
,,
,,
,
,
,
F为的中点,
,
在和中,
,
,
,
由(1)可知,,,
,
,
,
,
,
在中,,
故答案为:.
【点睛】本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,作辅助线构造全等三角形和相似三角形是解题关键.
22.(2023·四川泸州·统考中考真题)如图,,是正方形的边的三等分点,是对角线上的动点,当取得最小值时,的值是___________.
【答案】
【分析】作点F关于的对称点,连接交于点,此时取得最小值,过点作的垂线段,交于点K,根据题意可知点落在上,设正方形的边长为,求得的边长,证明,可得,即可解答.
【详解】解:作点F关于的对称点,连接交于点,过点作的垂线段,交于点K,
由题意得:此时落在上,且根据对称的性质,当P点与重合时取得最小值,
设正方形的边长为a,则,
四边形是正方形,
,,
,
,
,
,
,
,
,
,
,
当取得最小值时,的值是为,
故答案为:.
【点睛】本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.
23.(2023·山西·统考中考真题)如图,在四边形中,,对角线相交于点.若,则的长为__________.
【答案】
【分析】过点A作于点H,延长,交于点E,根据等腰三角形性质得出,根据勾股定理求出,证明,得出,根据等腰三角形性质得出,证明,得出,求出,根据勾股定理求出,根据,得出,即,求出结果即可.
【详解】解:过点A作于点H,延长,交于点E,如图所示:
则,
∵,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
即,
解得:,
∴,
∵,
∴,
即,
解得:.
故答案为:.
【点睛】本题主要考查了三角形外角的性质,等腰三角形的判定和性质,勾股定理,平行线分线段成比例,相似三角形的判定与性质,平行线的判定,解题的关键是作出辅助线,熟练掌握平行线分线段成比例定理及相似三角形的判定与性质.
三、解答题
24.(2023·湖南·统考中考真题)在中,是斜边上的高.
(1)证明:;
(2)若,求的长.
【答案】(1)见解析
(2)
【分析】(1)根据三角形高的定义得出,根据等角的余角相等,得出,结合公共角,即可得证;
(2)根据(1)的结论,利用相似三角形的性质即可求解.
【详解】(1)证明:∵是斜边上的高.
∴,
∴,
∴
又∵
∴,
(2)∵
∴,
又
∴.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
25.(2023·湖南·统考中考真题)如图,,点是线段上的一点,且.已知.
(1)证明:.
(2)求线段的长.
【答案】(1)见解析
(2)
【分析】(1)根据题意得出,,则,即可得证;
(2)根据(1)的结论,利用相似三角形的性质列出比例式,代入数据即可求解.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴,
∴;
(2)∵,
∴,
∵,
∴,
解得:.
【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.
26.(2023·四川眉山·统考中考真题)如图,中,点E是的中点,连接并延长交的延长线于点F.
(1)求证:;
(2)点G是线段上一点,满足,交于点H,若,求的长.
【答案】(1)见解析
(2)
【分析】(1)根据平行四边形的性质可得,,证明,推出,即可解答;
(2)通过平行四边形的性质证明,再通过(1)中的结论得到,最后证明,利用对应线段比相等,列方程即可解答.
【详解】(1)证明:四边形是平行四边形,
,,
,
是的中点,
,
,
,
∴,
;
(2)解:四边形是平行四边形,
,,
,,
,
,
,
,
,
,
设,则,
可得方程,
解得,
即的长为.
【点睛】本题考查了平行四边形的性质,等腰三角形的判定和性质,相似三角形的判定和性质,熟练运用上述性质证明三角形相似是解题的关键.
27.(2023·四川凉山·统考中考真题)如图,在中,对角线与相交于点,,过点作交于点.
(1)求证:;
(2)若,,求的长.
【答案】(1)见详解
(2)
【分析】(1)可证,从而可证四边形是菱形,即可得证;
(2)可求,再证,可得,即可求解.
【详解】(1)证明:,
,
四边形是平行四边形,
四边形是菱形,
.
(2)解:四边形是平行四边形,
,
,,
,
,
,
,
,
,
,
解得:.
【点睛】本题考查了平行四边形的性质,菱形的判定及性质,勾股定理,三角形相似的判定及性质,掌握相关的判定方法及性质是解题的关键.
28.(2023·江苏扬州·统考中考真题)如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.
(1)求证:四边形是平行四边形;
(2)若的面积为4,求的面积.
【答案】(1)见解析
(2)12
【分析】(1)根据平行四边形的性质,线段的中点平分线段,推出四边形,四边形均为平行四边形,进而得到:,即可得证;
(2)连接,推出,,进而得到,求出,再根据,即可得解.
【详解】(1)证明:∵,
∴,
∵点E、F、G、H分别是各边的中点,
∴,
∴四边形为平行四边形,
同理可得:四边形为平行四边形,
∴,
∴四边形是平行四边形;
(2)解:连接,
∵为的中点,
∴,
∴,
∴,
∴,
同理可得:
∴,
∴,
∵,
∴.
【点睛】本题考查平行四边形的判定和性质,三角形的中位线定理,相似三角形的判定和性质,熟练掌握平行四边形的性质,以及三角形的中位线定理,证明三角形相似,是解题的关键.
29.(2023·上海·统考中考真题)如图,在梯形中,点F,E分别在线段,上,且,
(1)求证:
(2)若,求证:
【答案】见解析
【分析】(1)先根据平行线的性质可得,再根据三角形的全等的判定可得,然后根据全等的三角形的性质即可得证;
(2)先根据全等三角形的性质可得,从而可得,再根据相似三角形的判定可得,然后根据相似三角形的性质即可得证.
【详解】(1)证明:,
,
在和中,,
,
.
(2)证明:,
,
,即,
在和中,,
,
,
由(1)已证:,
,
.
【点睛】本题考查了三角形全等的判定与性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.
专题21 图形的相似(共29题)--2023年中考数学真题分项汇编: 这是一份专题21 图形的相似(共29题)--2023年中考数学真题分项汇编,文件包含图形的相似共29题解析版pdf、图形的相似共29题学生版pdf等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
专题29 规律探究题(共14道)-2023年全国各地中考数学真题分项汇编(全国通用): 这是一份专题29 规律探究题(共14道)-2023年全国各地中考数学真题分项汇编(全国通用),文件包含专题29规律探究题共14道原卷版docx、专题29规律探究题共14道解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
专题21 图形的相似(共20道)-2023年全国各地中考数学真题分项汇编(全国通用): 这是一份专题21 图形的相似(共20道)-2023年全国各地中考数学真题分项汇编(全国通用),文件包含专题21图形的相似共20道原卷版docx、专题21图形的相似共20道解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。












