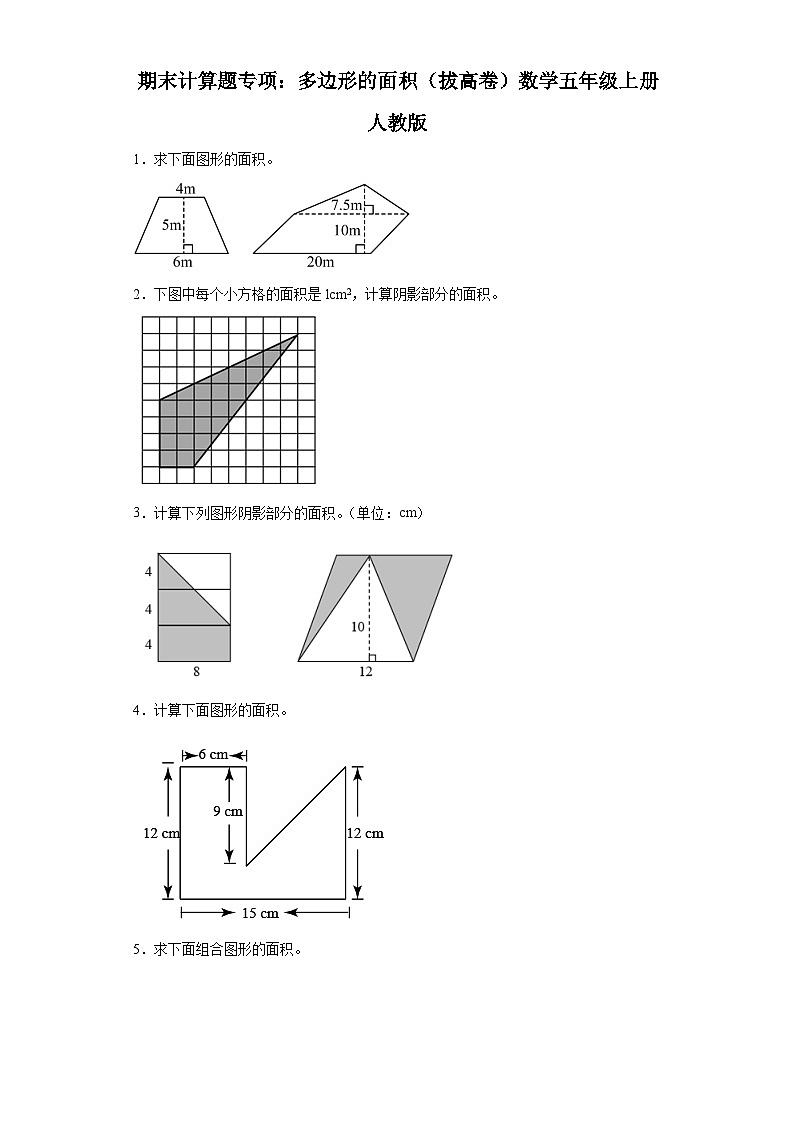
期末计算题专项：多边形的面积（拔高卷）数学五年级上册人教版

这是一份期末计算题专项：多边形的面积（拔高卷）数学五年级上册人教版，共12页。试卷主要包含了求下面图形的面积，计算下列图形阴影部分的面积，计算下面图形的面积，求下面组合图形的面积，计算下面图形中阴影部分的面积，求下列组合图形的面积，求下面图形阴影部分的面积，计算下面阴影部分的面积等内容，欢迎下载使用。


2．下图中每个小方格的面积是lcm2，计算阴影部分的面积。
3．计算下列图形阴影部分的面积。（单位：cm）
4．计算下面图形的面积。
5．求下面组合图形的面积。
（1） （2）
6．计算下面图形中阴影部分的面积。已知梯形的面积是30m2。
7．求下列组合图形的面积。
8．求下面图形阴影部分的面积。（单位：厘米）
9．计算下面阴影部分的面积。（单位：厘米）
10．求下面图形的面积。
11．计算下面图形阴影部分的面积。（单位：厘米）
（1） （2）
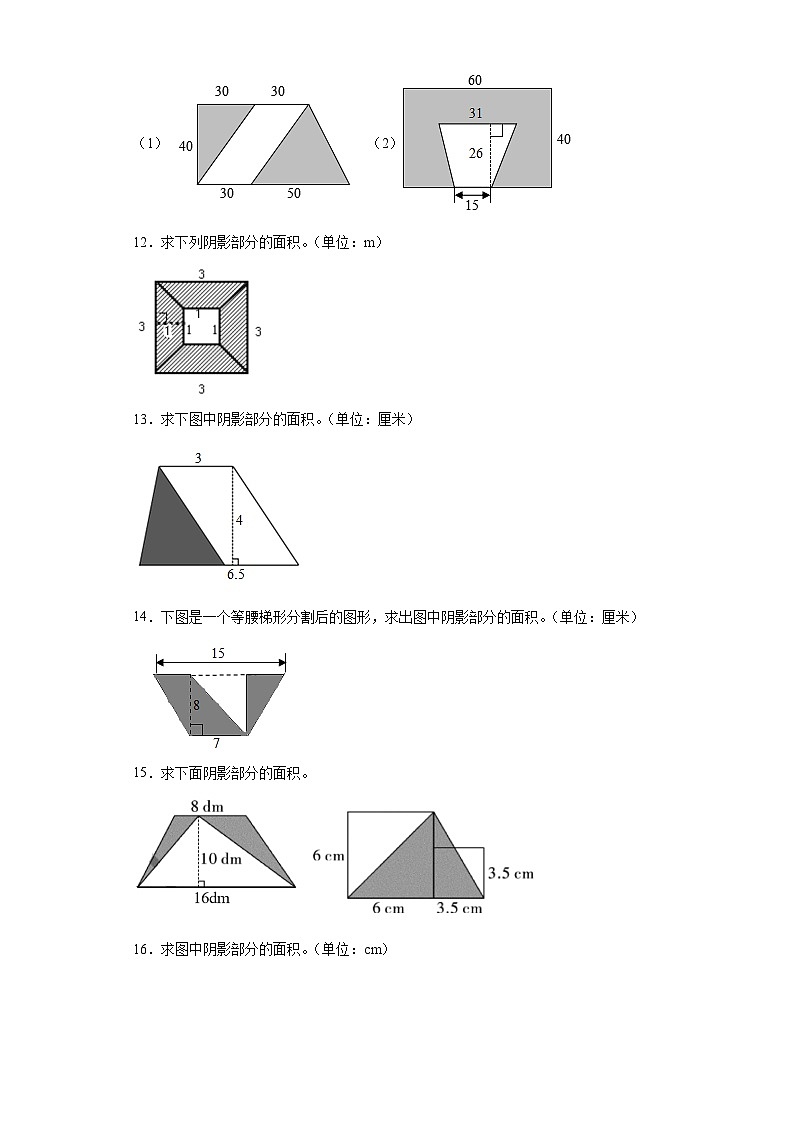
12．求下列阴影部分的面积。（单位：m）
13．求下图中阴影部分的面积。（单位：厘米）
14．下图是一个等腰梯形分割后的图形，求出图中阴影部分的面积。（单位：厘米）
15．求下面阴影部分的面积。
16．求图中阴影部分的面积。（单位：cm）
17．求阴影部分面积。（单位cm）
18．计算阴影部分的面积。
19．计算如图阴影部分的面积。
20．如图，两个正方形的边长分别为6厘米和4厘米，求阴影部分的面积。
参考答案：
1．25m2；275m2
【分析】根据梯形的面积公式：S＝（a＋b）h÷2，据此代入数值即可求出梯形的面积；图二的图形的面积等于平行四边形的面积加上三角形的面积，根据平行四边形的面积公式：S＝ah，三角形的面积公式：S＝ah÷2，据此进行计算即可。
【详解】（4＋6）×5÷2
＝10×5÷2
＝50÷2
＝25（m2）
20×10＋20×7.5÷2
＝200＋150÷2
＝200＋75
＝275（m2）
2．24平方厘米
【分析】如图，阴影部分的面积＝梯形面积＋三角形面积，据此列式计算。
【详解】（4＋5）×2÷2＋5×6÷2
＝9×2÷2＋15
＝9＋15
＝24（平方厘米）
3．64cm2；60cm2
【分析】观察图形可知，第一个阴影部分是一个上底为4cm，下底为（4×3）cm，高为8cm的梯形，根据梯形的面积公式求解即可；
第二个阴影部分的面积等于一个底为12cm，高为10cm的平行四边形面积减去一个底为12cm，高为10cm的三角形面积，根据平行四边形的面积公式和三角形的面积公式求解即可。
【详解】4×3＝12（cm）
（12＋4）×8÷2
＝16×8÷2
＝128÷2
＝64（cm2）
第一个阴影部分的面积是64cm2。
12×10－12×10÷2
＝120－60
＝60（cm2）
第二个阴影部分的面积是60cm2。
4．139.5平方厘米
【分析】可以将图形分成两部分计算面积，一部分为长方形，另一部分为梯形，长方形的长和宽题图中已经给出，梯形的上底是，下底是，梯形的高是，然后求梯形面积，两者相加即可。
【详解】；
；
；
＝135÷2
＝67.5（平方厘米）；
5．（1）48m2；（2）38cm2
【分析】（1）观察图形可知，该图形的面积等于平行四边形的面积减去三角形的面积，根据平行四边形的面积公式：S＝ab，三角形的面积公式：S＝ab÷2，据此代入数值进行计算即可；
（2）该图形的面积等于长为8cm，宽为3cm长方形的面积加上上底为（5－3）cm，下底是5cm，高是（8－4）cm的梯形的面积，再根据长方形的面积公式：S＝ab，梯形的面积公式：S＝（a＋b）h÷2，据此代入数值进行计算即可。
【详解】（1）12×6－12×4÷2
＝72－48÷2
＝72－24
＝48（m2）
（2）如图所示：
8×3＋（5－3＋5）×（8－4）÷2
＝24＋7×4÷2
＝24＋14
＝38（cm2）
6．9 m2
【分析】根据梯形的面积和上下底求出梯形的高，阴影部分三角形和梯形的高相等，利用三角形的面积公式求出阴影部分的面积。
【详解】30×2÷（6＋2＋12）
＝30×2÷20
＝60÷20
＝3（m）
6×3÷2＝9（m2）
所以，阴影部分的面积是9 m2。
7．26m2；1.65m2
【分析】第一个组合图形的面积＝梯形面积＋长方形面积，梯形面积＝（上底＋下底）×高÷2，长方形面积＝长×宽；
第二个组合图形的面积＝平行四边形面积＋三角形面积，平行四边形面积＝底×高，三角形面积＝底×高÷2。
【详解】（3＋5）×（6－2）÷2＋5×2
＝8×4÷2＋10
＝16＋10
＝26（m2）
1.5×0.8＋1.5×0.6÷2
＝1.2＋0.45
＝1.65（m2）
8．8400平方厘米；22平方厘米
【分析】（1）图1中，空白的梯形的高为（100－40）厘米，利用梯形的面积公式，求出空白的梯形的面积，利用正方形的面积公式，求出空白的正方形的面积，再用长方形的面积减去空白部分的面积，即是阴影部分的面积；
（2）图2利用正方形和三角形的面积公式，用大正方形和小正方形的面积之和，减去空白的大三角形的面积，即是阴影部分的面积。
【详解】（1）160×100－40×40－（40＋160）×（100－40）÷2
＝16000－1600－200×60÷2
＝14400－6000
＝8400（平方厘米）
（2）6×6＋4×4－6×（6＋4）÷2
＝36＋16－6×10÷2
＝52－30
＝22（平方厘米）
9．500平方厘米；2170平方厘米
【分析】（1）阴影部分的面积是一个底（50－30）厘米，高50厘米的三角形，根据三角形的面积＝底×高÷2，代入数据解答即可。
（2）阴影部分的面积是由一个长60厘米，宽40厘米的长方形减去一个上底为（60－22－22）厘米，下底30厘米，高10厘米的梯形，根据长方形的面积＝长×宽，梯形的面积＝（上底＋下底）×高÷2，代入数据即可解答。
【详解】（50－30）×50÷2
＝20×50÷2
＝1000÷2
＝500（平方厘米）
40×60－（60－22－22＋30）×10÷2
＝2400－（38－22＋30）×10÷2
＝2400－（16＋30）×10÷2
＝2400－46×10÷2
＝2400－460÷2
＝2400－230
＝2170（平方厘米）
10．372平方厘米；142平方厘米
【分析】（1）所求图形面积＝三角形的面积＋平行四边形的面积；
（2）所求图形面积＝梯形的面积－三角形的面积，据此解答。
【详解】（1）15×8÷2＋24×13
＝120÷2＋312
＝60＋312
＝372（平方厘米）
（2）（8.5＋18）×12÷2－8.5×4÷2
＝26.5×12÷2－8.5×4÷2
＝318÷2－34÷2
＝159－17
＝142（平方厘米）
11．（1）1600平方厘米；（2）1802平方厘米
【分析】（1）三角形的面积＝底×高÷2，据此先分别求出图中两个三角形的面积；再把两个三角形的面积相加求出阴影部分的面积。
（2）长方形的面积＝长×宽，梯形的面积＝（上底＋下底）×高÷2，据此先求出长是60厘米，宽是40厘米的长方形的面积；再求出图中梯形的面积；最后用长方形的面积减去梯形的面积求出阴影部分的面积。
【详解】（1）30×40÷2＋50×40÷2
＝1200÷2＋2000÷2
＝600＋1000
＝1600（平方厘米）
（2）60×40－（15＋31）×26÷2
＝2400－46×26÷2
＝2400－1196÷2
＝2400－598
＝1802（平方厘米）
12．8m2
【分析】大正方形的面积减小正方形的面积即为阴影部分的面积，据此解答。
【详解】3×3－1×1
＝9－1
＝8（m2）
【点睛】解答此题也可以求出上底是1m，下底是3m，高是1m的梯形的面积，再乘4求出阴影部分的面积。
13．7平方厘米
【分析】阴影部分的面积＝梯形的面积－平行四边形的面积，梯形面积＝（上底＋下底）×高÷2，平行四边形面积＝底×高，据此解答。
【详解】（3＋6.5）×4÷2－3×4
＝9.5×4÷2－3×4
＝19－12
＝7（平方厘米）
14．60平方厘米
【分析】依题意可得，阴影部分面积＝梯形面积－空白三角形面积，三角形的高等于梯形的高，底等于梯形的下底7厘米，据此解答。
【详解】（7＋15）×8÷2－（7×8÷2）
＝88－28
＝60（平方厘米）
答：图中阴影部分的面积为60平方厘米。
【点睛】灵活运用平面图形的面积公式是解题关键。
15．40dm2；28.5cm2
【分析】图一，阴影部分面积＝梯形面积－三角形面积；
图二，阴影部分面积＝三角形面积。
梯形面积＝（上底＋下底）×高÷2；三角形面积＝底×高÷2。
【详解】（16＋8）×10÷2－16×10÷2
＝24×10÷2－80
＝120－80
＝40（dm2）
（6＋3.5）×6÷2
＝9.5×6÷2
＝57÷2
＝28.5（cm2）
图一，阴影部分的面积是40dm2；图二，阴影部分的面积是28.5cm2。
16．30cm2
【分析】阴影部分的面积＝梯形面积－三角形面积，根据梯形的面积＝（上底＋下底）×高÷2，三角形的面积＝底×高÷2，代入数据进行计算即可。
【详解】梯形的面积：（4＋8）×6÷2
＝12×6÷2
＝72÷2
＝36（cm2）
三角形的面积：4×3÷2
＝12÷2
＝6（cm2）
阴影部分的面积：36－6＝30（cm2）
17．35平方厘米
【分析】阴影部分是一个上底为3，下底为3＋8，高为5的梯形，据此代入梯形面积公式求解即可。
【详解】（3＋3＋8）×5÷2
＝14×5÷2
＝35（平方厘米）
18．35.28cm2
【分析】阴影部分是一个梯形，上底为9cm，下底为9－5.4＝3.6cm，高为5.6，据此代入数据解答即可。
【详解】梯形的下底：9－5.4＝3.6（cm）
（9＋3.6）×5.6÷2
＝12.6×5.6÷2
＝70.56÷2
＝35.28（cm2）
19．2350平方米
【分析】观察图形可知，阴影部分的面积等于长方形面积加上三角形的面积；再根据长方形的面积公式：S＝ab，三角形的面积公式：S＝ah÷2，据此代入数值进行计算即可。
【详解】70×25＋40×30÷2
＝1750＋600
＝2350（平方米）
则阴影部分的面积是2350平方米。
20．14平方厘米
【分析】如图所示，阴影部分的面积＝大正方形的面积＋小正方形的面积－大正方形面积的一半－（大正方形的边长＋小正方形的边长）×小正方形的边长÷2，两个正方形的边长已知，代入此等式，即可求得阴影部分的面积。
【详解】6×6＋4×4－6×6÷2－（6＋4）×4÷2
＝36＋16－18－20
＝52－38
＝14（平方厘米）
【点睛】解答此题的关键是：弄清楚阴影部可以用哪些图形转化而成，从而可以求出其面积。