苏科版数学九年级下册 6.1图上距离与实际距离PPT课件

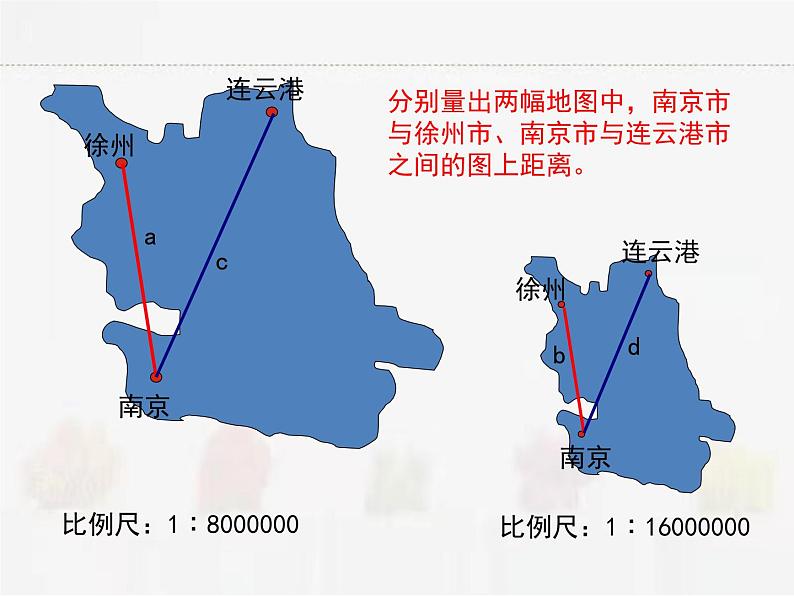
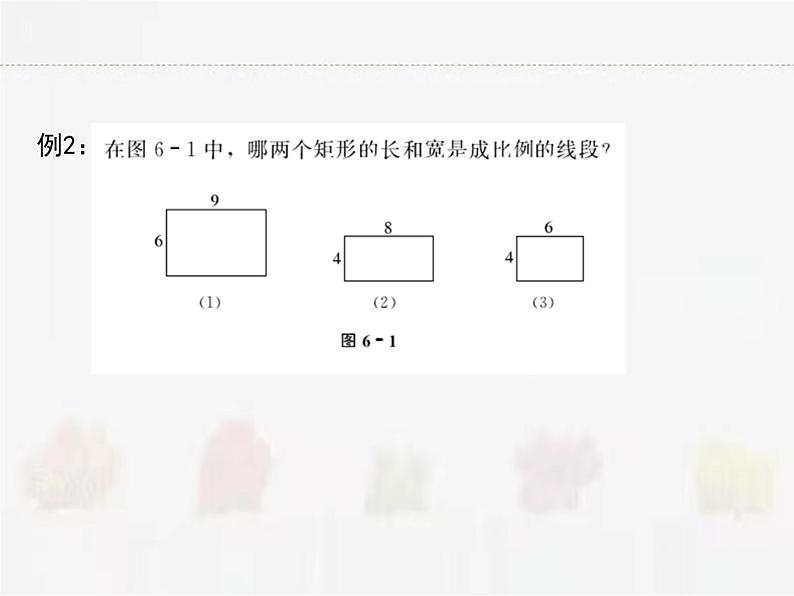
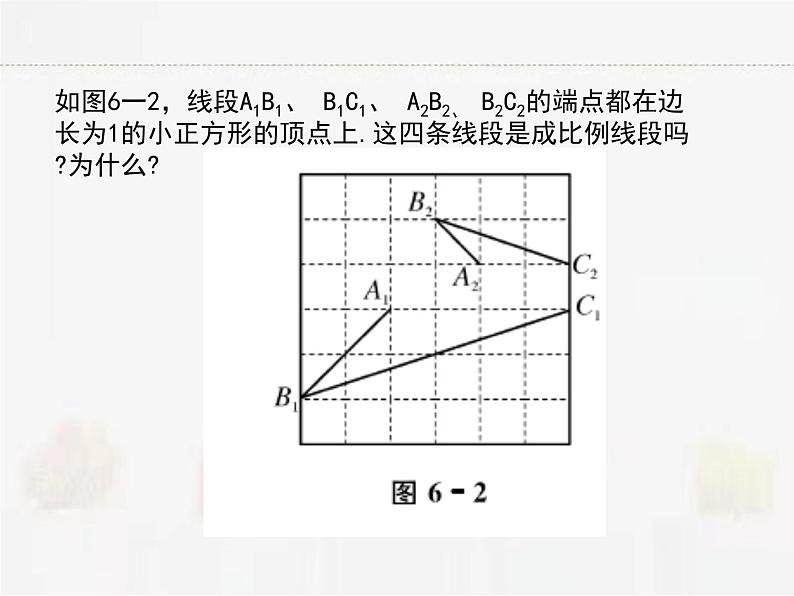
第6章 图形的相似6.1图上距离与实际距离比例尺：1∶8000000比例尺：1∶16000000分别量出两幅地图中，南京市与徐州市、南京市与连云港市之间的图上距离。abcd在上面的两幅江苏省地图中，设连接南京与徐州的线段分别为a,b，它们的比(即a与b的长度的比，为a:b或 ，连接南京与连云港的线段分别为c、d，它们的比为c:d或 ， 这两个比值相等吗?一、两条线段的比和成比例线段的概念：　1、两条线段长度的比叫做两条线段的比　　知识易学小结：①线段的比即长度的比，单位必须一致；②线段的长总是一个正数，故线段比不可能是负数和零.例1、甲、乙两城市之间的距离为920km，画在地图上的距离为92cm，求图上距离与实际距离的比（比例尺).2、成比例线段在四条线段中，如果两条线段的比等于另外两条线段的比，那么称这四条线段成比例线段.符号语言：若 ，则线段a、b、c、d成比例，反之，若则线段a、b、c、d成比例， 则 .　注意：（1）成比例线段是4条线段之间的关系.（2）线段a、b、c、d成比例亦可说a、b、c、d是成比例线段.例2：例3、已知a、b、c、d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，求线段d的长.若a、c、d、b是成比例线段，其余条件不变，求d长.小结：成比例的四条线段是有顺序的如：若 ，则a、b、c、d是成比例线段；若 ，则c、b、d、a是成比例线段.如图6一2，线段A1B1、 B1C1、 A2B2、 B2C2的端点都在边长为1的小正方形的顶点上.这四条线段是成比例线段吗?为什么?已知四条线段a、b、c、d的长度，试判断它们是否成比例？（1）a＝16cm，b＝8cm，c＝5cm，d＝10cm（2）a＝8cm，b＝0.05cm，c＝0.6dm，d＝10cm小结：判断四条线段是否成比例，首先统一四条线段的长度单位，再分别计算两条较小线段的比及两条较大线段的比，如果两个比相等，那么这四条线段成比例，如果这两个比不等，那么这四条线段不成比例.二、比例的性质1、比例的基本性质　练习：(1)如果 ，那么 ＝＿＿；　　(2)由ad＝bc，写成的比例式中，错误的是（　　）　　　2、比例中项　　在 中，如果b＝c，即 ， 那么b2＝ac，这时我们把b叫作a和c的比例中项.例1（1）已知x＝8，y＝2，则x与y的比例中项是＿＿＿＿＿；（2）已知线段a＝5cm，b＝3cm，则线段a＋b与a－b的比例中项是＿＿＿＿＿.小结：比例中项，若是线段，则为正；若是数，则可正可负.例2 已知 ，求 和 的值.可以采用设k法例4 已知a：b：c＝3：2：4，求：(2）2a＋3b－c＝24，求:3a－2b－c.例5 若x：y＝3：5，y：z＝2：3，求x：y ：z 的值.1. 已知线段a、b满足 ，则 ＝＿＿＿， ＝＿＿＿＿.2. 若a＝12，b＝3，那么a、b的比例中项c＝＿＿＿.3. 若b是a、c的比例中项，且a＝2cm，c＝8cm，b＝＿＿＿.练一练4.兴华机械厂要加工一种精密零件，该零件长30mm，现要把它放大画在图纸上，若按照比例尺为10：1，那么该零件在图纸上有＿＿＿＿cm.5.线段AB＝0.2cm，CD＝10m，则AB：CD＝＿＿＿＿.6.若a、b、d、c是成比例线段，其中a＝5cm，b＝3cm，c＝2cm，则线段d＝＿＿＿＿＿cm.7. 已知矩形ABCD中，AB＝12，AD＝5，则 ＝＿＿＿＿.