初中数学苏科版九年级下册6.5 相似三角形的性质第1课时教学设计

这是一份初中数学苏科版九年级下册6.5 相似三角形的性质第1课时教学设计，共8页。教案主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

学习目标：
1．探索相似三角形的性质，会运用相似三角形的性质解决有关的问题．
2．发展学生合情推理和有条理的表达能力．
学习重点：
理解相似三角形的性质，能运用相似三角形的性质解决有关的问题．
学习难点：
能根据已知条件，构建数学模型，有条理的说理．
学习过程：
复习回顾：
如图，△ABC∽△A′B′C′，你能得到什么？
B
B
C
A
A′
B′
C′
C
A
B
F
D
E
合作探究：
想一想：
1．如图，点D、E、F分别是△ABC各边的中点，
（1）△DEF与△ABC相似吗？为什么？
（2）这两个三角形的相似比是多少？
（3）这两个三角形的周长、面积有什么关系？
C
A
B
E
D
F
M
N
P
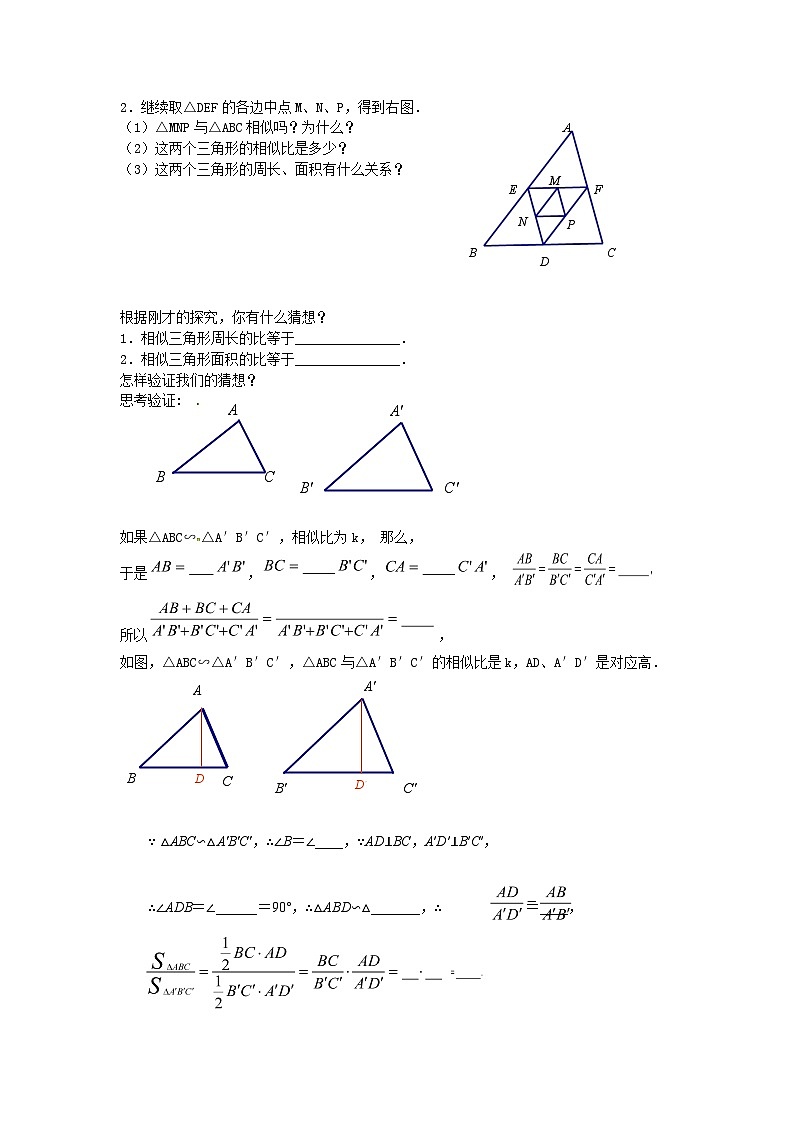
2．继续取△DEF的各边中点M、N、P，得到右图．
（1）△MNP与△ABC相似吗？为什么？
（2）这两个三角形的相似比是多少？
（3）这两个三角形的周长、面积有什么关系？
根据刚才的探究，你有什么猜想？
1．相似三角形周长的比等于_______________．
2．相似三角形面积的比等于_______________．
怎样验证我们的猜想？
A
A′
思考验证:
B
C
C′
B′
如果△ABC∽△A′B′C′，相似比为k， 那么，
于是，，，
所以，
如图，△ABC∽△A′B′C′，△ABC与△A′B′C′的相似比是k，AD、A′D′是对应高．
A
A′
B
D
C
D’
C′
B′
∵ △ABC∽△A'B'C'，∴∠B＝∠____，∵AD⊥BC，A′D′⊥B′C′，
∴∠ADB＝∠______＝90°，∴△ABD∽△_______，∴ ＝____，

结论：
1．相似三角形周长的比等于________________．
2．相似三角形面积的比等于________________．
类似的，我们还能得到：
1．相似多边形周长的比等于________________．
2．相似多边形面积的比等于________________．
试一试：
1．两个相似三角形的相似比为2:3，它们的对应边之比为 ，周长之比为 ，
面积之比为 ．
2．若两个三角形面积之比为16:9，则它们的周长之比为_____．
3．两个相似多边形的面积之比为1:4，周长之差为6，则这两个相似多边形的周长分别为_____．
议一议：
例题分析：
例1、在比例尺为1:500的地图上，测得一个三角形地块ABC的周长为12 cm，面积为6cm2，求这个地块的实际周长和面积．
例2、若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,[来源
则DE= cm。
例3、如图，把△ABC沿AB边平移到△DEF的位置，它们重叠部分的面积是△ABC面积的一半，若AB=2，求此三角形移动的距离BE的长。
练一练：
1．相似三角形对应边的比值为0.4，那么相似比为 , 周长的比为 ，面积的比为＿＿．
2．已知△ABC的三边长分别为3、4、5，与它相似的△A′B′C′的最大边长为15．
求△A′B′C′的面积．
3．在一张比例尺为5:1的图纸上，量得一个零部件的周长是3.6cm，面积是6cm2，求这个零部件的实际周长和面积．
拓展延伸：
某施工队在道路拓宽施工时遇到这样一个问题，马路旁边原有一个面积为100m2，周长为80m的三角形绿化地，由于马路拓宽，绿地被削去了一个角，变成了一个梯形，原绿化地一边AB的长由原来的30m缩短成18m．现在的问题是：被削去的部分面积有多大？它的周长是多少？
小结：
课堂作业：
课后练习：
一、选择题
1．已知△ABC∽△DEF，且AB：DE=1：2．则△ABC的面积与△DEF的面积之比为 ( )
A．1：2 B．1：4 C．2：1 D．4：1
2．若一个图形的面积为2，那么将与它成中心对称的图形放大为原来的两倍后的图形面积为 ( )
A．8 B．6 C．4 D．2
3．若△ABC∽△DEF，且△ABC与△DEF的相似比为1：2．则△ABC与
△DEF的周长比为 ( )
A．1：4 B．1：2 C．2：1 D．
4．两个相似多边形的面积之比为1：3，则它们的周长之比为 ( )
A．1：3 B．1：9 C． D．2：3
5．在△ABC和△DEF中，AB=2DE，AC=2DF，∠A=∠D，如果△ABC的周长是16，面积是12，那么△DEF的周长、面积分别为 ( )
A．8、3 B．8、6 C．4、3 D．4、6
二、填空题
6．在△ABC中，AB=12 cm，BC=18 cm，CA=24 cm．另一个与它相似的△A′B′C′的周长为81 cm，那么△A′B′C′的最短边长为________cm．
7．如图，在△ABC中，DE∥BC，AE：EC=1：2，则S△ADE：S△ABC=________．
8．若两个相似多边形的面积之比为1：4．周长之差为6，则这两个相似多边形的周长分别是_________．
9．如图，在△ABC中，DE∥BC，若AD=1，DE=2，BD=3，则BC=_______．
三、解答题
10．如图是测量小破璃管口径的量具ABC，AB的长为10cm，AC被分为60等份．如果小玻璃管口DE正好对着量具上20等份处(DE∥AB)，那么小玻璃管口径DE是多大?
11．两个相似三角形的一对对应边长分别为20 cm、35 cm．如果它们的周长之差为63 cm，
求这两个三角形的周长．
12．如图，△ABC ∽△DEF，且△ABC和△DEF的相似比为k．点M、N与点P、Q分别在AB、AC与DE、DF上，且AB：AM=DE：DP，AC：AN=DF：DQ试说明：MN：PQ=k．
13．如图(1)，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上的一点，连接BO交AD于点F，OE⊥OB交BC边于点E．
(1)试说明：△ABF∽△COE．
(2)如图(2)，当O为AC边的中点，且时，求的值．
(3)当O为AC边的中点，时，请直接写出的值．
参考答案
1．B 2．A 3．B 4．C 5．A
6．18
7．1：9
8．6和12
9．8
10．
11．两个三角形的周长分别是84 cm、147 cm
12．因为△ABC∽△DEF，所以∠A=∠D，AC：AB=DF：DE．又因为AB：AM=DE：DP，AC：AN=DF：DQ．所以AM：AN=DP：DQ．所以△AMN∽△DPQ所以MN：PQ=AM：DP=AB：DE=k
13．(1)因为AD⊥BC，所以∠DAC+∠C=90°．又因为∠BAC=90°，所以∠BAF=∠C．因为OE⊥OB，所以∠BOA+∠COE=90°．因为∠BOA+∠ABF=90°，所以∠ABF=∠CDE．所以△ABF∽△COE [来源:学.科.网]
(2)作OG⊥AC，交AD的延长线于点G．因为AC=2AB，O是AC边的中点，所以AB=OC=OA．由(1)有△ABF∽△COE．所以△ABF≌△COE所以BF=OE．因为∠BAD+∠DAC=90°，∠DAB+∠ABD=90°，所以∠DAC=∠ABD．又因为∠BAC=∠AOG=90°，AB=OA，所以△ABC∽△OAG．所以OG=AC=2AB．因为OG⊥AC，所以AB∥OG．所以△ABF∽△GOF．所以，
(3)