数学九年级下册6.5 相似三角形的性质第2课时教案

这是一份数学九年级下册6.5 相似三角形的性质第2课时教案，共9页。教案主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

学习目标：
1．运用类比的思想方法，通过实践探索得出：相似三角形对应线段（高、中线、角平分线）的比等于相似比；
2．会运用相似三角形对应高的比与相似比的性质解决有关问题；
3．经历“操作——观察——探索——说理”的数学活动过程，发展合情推理和有条理的表达能力．
学习重点：探索得出相似三角形，对应线段的比等于相似比．
学习难点：利用相似三角形对应高的比与相似比的性质解决问题．
学习过程：
复习回顾：
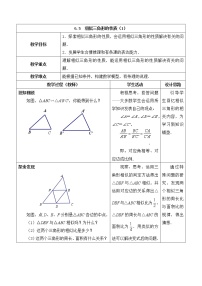
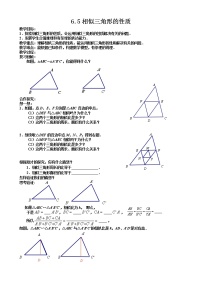
如图，△ABC∽△A′B′C′，△ABC与△A′B′C′的相似比是2:3，则△ABC与△A’B’C’的面积比是多少？你的依据是什么？
A
A′
B′
B
C
C′
回顾“相似三角形的面积比等于相似比的平方”这个结论的探究过程，你有什么发现？
A′
A
如图，△ABC∽△A′B′C′，△ABC与△A′B′C′的相似比是k，AD、A′D′是对应高．
D’
C
B
D
C′
B′
∵ △ABC∽△A'B'C'，∴∠B＝∠____，∵AD⊥BC，A′D′⊥B′C′，
∴∠ADB＝∠______＝90°，∴△ABD∽△_______，∴ ＝____，

结论：
相似三角形对应高的比等于___________．
三角形中的特殊线段还有哪些？它们是否也具有类似的性质呢？你有何猜想？
合作探究：
问题一：
△ABC∽△A′B′C′，AD和A′D′分别是△ABC和△A′B′C′的中线，设相似比为k，那么
C
A
B
D
C′
A′
D′
B′
结论：相似三角形对应中线的比等于___________．
问题二：
C′
A′
D′
B′
△ABC∽△A′B′C′，AD和A′D′分别是△ABC和△A′B′C′的角平分线，设相似比为k，
C
A
B
D
那么
∵△ABC∽△A′B′C′，
∴∠BAC＝∠_______，∠B＝_________．
∵AD和A′D′分别是△ABC和△A′B′C′的角平分线，
，
∴∠BAD＝∠________，∴△ABD∽△________，∴．
结论：相似三角形对应角平分线的比等于___________．
一般地，如果△ABC∽△ A'B'C'，相似比为k，点D、D'分别在BC、B'C'上，且 ， 那么你能类比刚才的方法说理吗？

总结：相似三角形对应_____________的比等于相似比．
例题分析：
例1、如图，D、E分别在AC、AB上，∠ADE＝∠B，AF⊥BC，AG⊥DE，垂足分别是F、G，若AD＝3，AB＝5，求：
的值．
△ADE与△ABC的周长的比，面积的比．
练一练：
1．两个相似三角形的相似比为2:3，它们的对应角平分线之比为_______，周长之比为_______，面积之比为_________
2．若两个相似三角形面积之比为16:9，则它们的对高之比为_____，对应中线之比为_____
3．如图，△ABC∽△DBA，D为BC上一点，E、F分别是AC、AD的中点，且AB＝28cm，BC＝36cm，则BE:BF＝________
4．如图，梯形ABCD中，AD∥BC，AD＝36cm，BC＝60cm，延长两腰BA，CD交于点O，OF⊥BC，交AD于E，EF＝32cm，求OF的长．
拓展延伸：
如图，△ABC是一块锐角三角形的余料，边长BC＝120mm，高AD＝80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点在AB、AC上，这个正方形的零件的边长为多少？
小结：
课堂作业：
课后练习：
一、选择题
1．如图是小孔成像原理的示意图，这支蜡烛在暗盒中所成的像CD的长是1 cm，则像CD到小孔O的距离为 ( )
A．1 cm B．2 cm C．3 cm D．4 cm
2．如图，铁道口的栏杆短臂长1 m，长臂长16 m，当短臂的端点A下降0．5 m时，长臂的端点B应升高 ( )
A．0．5 m B．1 m C．8 m D．16 m
3．如图，圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后，在地面上形成阴影．已知桌面的直径为1．2 m，桌面距离地面1 m．若灯泡距离地面3 m，则地面上阴影部分的面积为 ( )
A．0．36m2 B．0．81m2 C．2m2 D．3．24m2
4．一张等腰三角形纸片，底边长15 cm，底边上的高长22．5 cm．现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是 ( )
A．第4张 B．第5张 C．第6张 D．第7张
二、填空题
5．如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB的高度为36 cm，那么它在暗盒中所成的像CD的高度应为________cm．
6．如图，电影胶片上每一个图片的规格为3．5 cm×3．5 cm，放映屏幕的规格为2 m×2 m，若放映机的光源S距胶片20 cm，那么光源S距屏幕________m时，放映的图像刚好布满整个屏幕．
7．顺次连接三角形三边上的中点所构成的三角形的高与原三角形对应高的比为_______．
8．如图，点M是△ABC内一点．过点M分别作直线平行于△ABC的各边，所形成的三个小三角形(图中阴影部分)的面积分别是4、9和49，则△ABC的面积是________．
三、解答题
9．如图，DE∥BC，AG⊥BC于点G，交DE于点F．若AD=6，BD=4，AG=8，求AF的长．
10．如图，火焰AC通过纸板EF上的一个小孔O射到屏幕上形成倒立的像，像的长度BD=2 cm，0．4=60 cm，OB=20 cm，求火焰AC的长．
11．如图，在四边形ABCD中，AC平分∠BAD，BC⊥AC，CD⊥AD，且AB=18，AC=12．
(1)求AD的长．
(2)若DE⊥AC，CF⊥AB，垂足分别为E、F，求的值．
12．有一块三角形铁片ABC，BC=12 cm．高AH=8 cm，按图(1)、(2)两种设计方案把它加工成一块矩形铁片DEFG，且要求矩形的长是宽的2倍，为了减少浪费，加工成的矩形铁片的面积应尽量大些．请你通过计算判断(1)、(2)两种设计方案哪个更好．
参考答案
1．B 2．解：设长臂端点升高x米，则，∴x=8．C
3．解：如图，根据常识桌面与地面平行，所以，△ADE∽△ABC，
∴=，即=，解得BC=1.8，
所以，地面上阴影部分的面积=π•（）2=0.81π平方米，B
4．设剪的是第x张，则，x=6，故选C.
5．16 6． 7．1：2
8．解：过M作BC平行线交AB、AC于D、E，过M作AC平行线交AB、BC于F、H，过
M作AB平行线交AC、BC于I、G，∵△1、△2的面积比为4：9，△1、△3的面积比为4：49，
∴它们边长比为2：3：7，
又∵四边形BDMG与四边形CEMH为平行四边形，
∴DM=BG，EM=CH，设DM为2x，
∴BC=（BG+GH+CH）=12x，∴BC：DM=6：1，
S△ABC：S△FDM=36：1，∴S△ABC=4×36=144．
9．
10．AC=6 cm
11．(1)AD=8 (2)
12．(1)种方案更好一些．设方案(1)中DE=x．根据题意，得．解得，，面积为；设方案(2)中DE=2y．根据题意，得．解得y=3，面积为18．因为，所以(1)种方案更好一些