初中数学3.3 相似图形优秀练习

这是一份初中数学3.3 相似图形优秀练习，文件包含课时练湘教版2023-2024学年初中数学九年级上册35相似图形的应用同步分层训练基础卷教师版docx、课时练湘教版2023-2024学年初中数学九年级上册35相似图形的应用同步分层训练基础卷学生版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
一、选择题
1．（2023·宜宾模拟）如图，在平行四边形ABCD中，点E在边DC上，DE：EC＝4：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（ ）
A．4：5B．9：16C．16：25D．3：5
2．（2023九上·宜宾期末）如图，它是物理学中小孔成像的原理示意图，已知物体AB=30，根据图中尺寸(AB∥CD)，则CD的长应是（ ）
A．15B．30C．20D．10
3．（2021九上·长清期中）如图所示，某校数学兴趣小组利用标杆BE测量物的高度，已知标杆BE高1.5m，测得AB＝1.2m，AC＝14m，则建筑物CD的高是（ ）
A．17.5mB．17mC．16.5mD．18m
4．（2021·江州模拟）如图，圆桌正上方的灯泡O发出的光线照射桌面后，在地面上形成圆形阴影.已知桌面的直径为1.2m，桌面距离地面1m，若灯泡O距离地面3m，则地面上阴影部分的面积为（ ）
A．0.36πm2B．0.81πm2C．1.44πm2D．3.24πm2
5．（2023·威海）常言道：失之毫厘，谬以千里．当人们向太空发射火箭或者描述星际位置时，需要非常准确的数据．1″的角真的很小．把整个圆等分成360份，每份这样的弧所对的圆心角的度数是1°．1°=60′=3600″．若一个等腰三角形的腰长为1千米，底边长为4.848毫米，则其顶角的度数就是1″．太阳到地球的平均距离大约为1.5×108千米．若以太阳到地球的平均距离为腰长，则顶角为1″的等腰三角形底边长为（ ）
A．24.24千米B．72.72千米C．242.4千米D．727.2千米
6．（2023·隆昌模拟）如图所示，某校数学兴趣小组利用标杆BE测量建筑物的高度，已知标杆BE高为1.5m，测得AB＝3m，BC＝7m，则建筑物CD的高是（ ）m
A．3.5B．4C．4.5D．5
7．（2023·长丰模拟）如图，△ABC是等边三角形，△ABD是等腰直角三角形，∠BAD=90°，AE⊥BD于点E，连接CD分别交AE，AB于点F，G，过点A作AH⊥CD分别交CD，BD于点P，H，则下列结论不正确的是（ ）
A．∠BAC=4∠ADCB．DF=AH
C．BH=2PFD．若2CG=3BG，则3AG=2FG
8．（2023九下·慈溪月考）有一块锐角三角形余料△ABC，边BC的长为20cm，BC边上的高为16cm，现要把它分割成若干个邻边长分别为5cm和4cm的小长方形零件，分割方式如图所示（分割线的耗料不计），使最底层的小长方形的长为5cm的边在BC上，则按如图方式分割成的小长方形零件最多有（ ）
A．5个B．6个C．7个D．8个
二、填空题
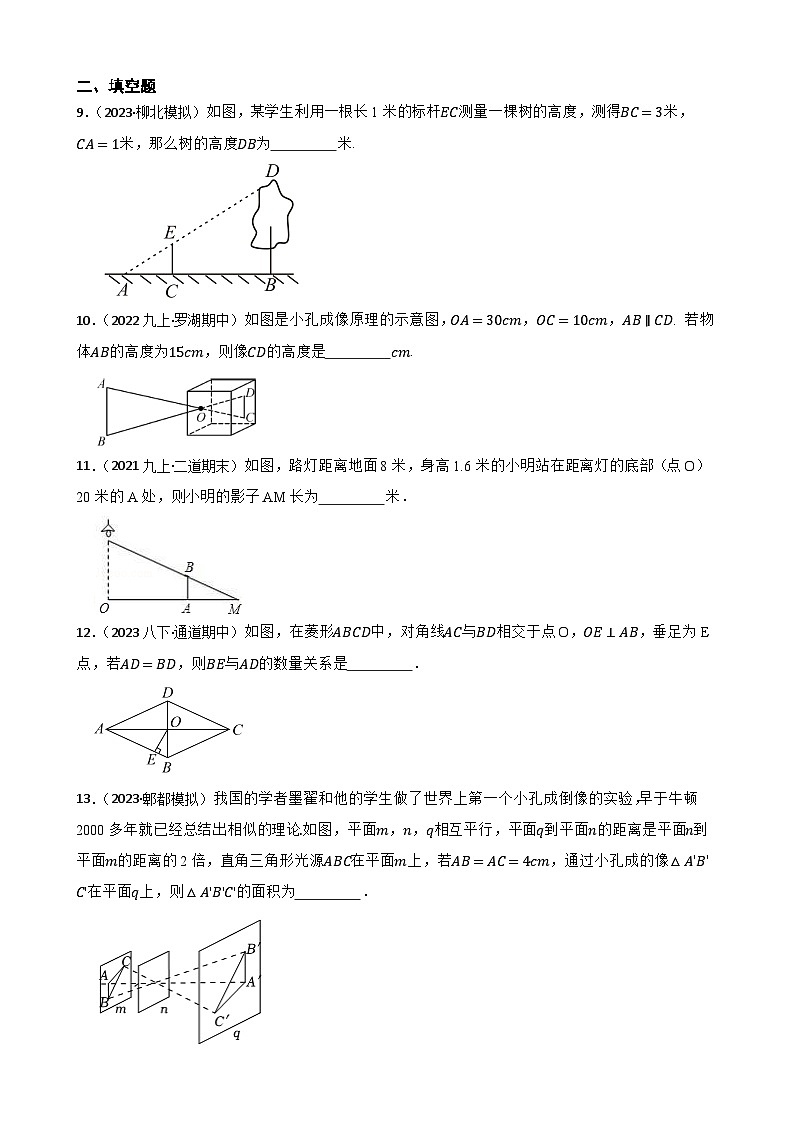
9．（2023·柳北模拟）如图，某学生利用一根长1米的标杆EC测量一棵树的高度，测得BC=3米，CA=1米，那么树的高度DB为 米.
10．（2022九上·罗湖期中）如图是小孔成像原理的示意图，OA=30cm，OC=10cm，AB∥CD. 若物体AB的高度为15cm，则像CD的高度是 cm.
11．（2021九上·二道期末）如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为 米．
12．（2023八下·通道期中）如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E点，若AD=BD，则BE与AD的数量关系是 ．
13．（2023·郫都模拟）我国的学者墨翟和他的学生做了世界上第一个小孔成倒像的实验，早于牛顿2000多年就已经总结出相似的理论.如图，平面m，n，q相互平行，平面q到平面n的距离是平面n到平面m的距离的2倍，直角三角形光源ABC在平面m上，若AB=AC=4cm，通过小孔成的像△A′B′C′在平面q上，则△A′B′C′的面积为 ．
三、解答题
14．（2022·芜湖模拟）《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D点观察井内水岸C点，视线DC与井口的直径AB交于点E．如果测得AB＝1.8米，BD＝1米，BE＝0.2米．请求出井深AC的长．
15．（2023·西安模拟）铜川市【铜川1958】雕塑群体展现了铜川1958年因煤设市、因煤而兴的一个时代的记忆．某数学兴趣小组的同学计划测量雕塑上方人物铜像的高度AB．如图，小组同学在D处竖立一根可伸缩的标杆，甲站在G处恰好看到标杆顶端E和人物铜像底端B在一条直线上，DG=3米，CD=33米；甲站在G处不动，小组同学调整标杆的高度，当标杆的顶点恰好在F处时，甲看到标杆顶端F和人物铜像顶端A在一条直线上，EF=1米，AC⊥CG，FD⊥CG，HG⊥CG，点B在AC上，点E在DF上，点C、D、G在一条水平线上，请根据以上测量数据与方法求出人物铜像的高度AB．
四、综合题
16．（2023·玉溪模拟）如图，⊙O是△ABC的外接圆，BC是⊙O的直径，点D是⊙O外一点，AC平分∠BCD，过点A作直线CD的垂线，垂足为点D，连接AD，点E是AB的中点，连接OE．
（1）求证：AD是⊙O的切线；
（2）若⊙O的直径为10，OE=3，求CD的长．
17．（2023·临海模拟）如图1，点光源O射出光线沿直线传播，将胶片上的建筑物图片AB投影到与胶片平行的屏幕上，形成影像CD.已知AB=0.3dm，胶片与屏幕的距离EF为定值，设点光源到胶片的距离OE长为x（单位：dm），CD长为y（单位：dm），当x=6时，y=4.3.
（1）求EF的长.
（2）求y关于x的函数解析式，在图2中画出图像，并写出至少一条该函数性质.
（3）若要求CD不小于3dm，求OE的取值范围.
答案解析部分
1．【答案】C
【知识点】相似三角形的应用
【解析】【解答】解：设DE=4k，EC=k，则CD=5k，
∵四边形ABCD是平行四边形，∴AB=CD=5k，DE⊥AB，
△DEF~△BAF，
S△DEFS△BAF=(DEAB)2=(4k5k)2=1625，
故答案为C
【分析】设未知数k，由平行四边形推出，AB=CD，DE∥AB，得出△DEF~△BAF，推出S△DEFS△BAF=(DEAB)2。
2．【答案】D
【知识点】相似三角形的应用
【解析】【解答】解：依题意，△ODC∽△OAB
∴ABCD=3612
∵AB=30
∴CD=13×30=10，
故答案为：D.
【分析】根据平行于三角形一边的直线，截其它两边的延长线，所截的三角形与原三角形相似可得△ODC∽△OAB，根据相似三角形对应边上高之比等于相似比建立方程，求解即可.
3．【答案】A
【知识点】相似三角形的应用
【解析】【解答】解：∵EB⊥AC，DC⊥AC，
∴EB // DC，
∴△ABE∽△ACD，
∴ABAC=BECD ，
∵BE＝1.5m，AB＝1.2m，AC＝14m，
∴1.214=1.5DC ，
解得，DC＝17.5（m），
即建筑物CD的高是17.5m，
故答案为：A．
【分析】由△ABE∽△ACD可得关系式ABAC=BECD即可求解。
4．【答案】B
【知识点】相似三角形的应用
【解析】【解答】解：如图设C，D分别是桌面和其地面影子的圆心，CB∥AD，
∴△OBC∽△OAD
∴CBAD=OCOD ，而OD=3，CD=1，
∴OC=OD-CD=3-1=2，BC= 12 ×1.2=0.6
∴0.6AD=23 ，
∴AD=0.9 S⊙D=π×0.92=0.81πm2，这样地面上阴影部分的面积为0.81πm2.
【分析】根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交，所构成的三角形与原三角形相似”可得△OBC∽△OAD，由相似三角形的性质可得比例式BCAD=OCOD，结合已知求出AD的值，再根据圆的面积S=πR2可求解.
5．【答案】D
【知识点】相似三角形的判定与性质；相似三角形的应用
【解析】【解答】解：设以太阳到地球的平均距离为腰长，则顶角为1″的等腰三角形底边长为amm，由题意得1.5×1081=a4.848，
解得a=7.272×108，
∴顶角为1″的等腰三角形底边长为727.2千米，
故答案为：D
【分析】设以太阳到地球的平均距离为腰长，则顶角为1″的等腰三角形底边长为amm，进而根据相似三角形的判定与性质即可列出方程，从而即可求出a，进而即可求解。
6．【答案】D
【知识点】相似三角形的应用
【解析】【解答】根据题意可得：△ABE∽△ACD，
∴ABAC=BECD，
∵AB=3m，BC=7m，
∴AC=AB+BC=10m，
∴310=1.5CD，
∴CD=5，
故答案为：D.
【分析】先证出△ABE∽△ACD，再利用相似三角形的性质可得ABAC=BECD，最后将数据代入求出CD的长即可。
7．【答案】D
【知识点】三角形全等的判定；相似三角形的应用
【解析】【解答】∵△ABC为等边三角形，△ABD为等腰直角三角形，
∴∠BAC＝60°，∠BAD＝90°，AC＝AB＝AD，∠ADB＝∠ABD＝45°，
∴△CAD是等腰三角形，∠CAD＝150°，
∴∠ADC＝15°，∠BAC＝4∠ADC，
故选项A正确；
∵∠ADB＝∠ABD＝45°，∠ADC＝15°，
∴∠EDF＝30°，
又∵AH⊥CD，AE⊥BD且∠AFG＝60°，
∴∠FAP＝30°，∠DAE＝45°，
∴∠BAH＝∠ADC＝15°，
在△ADF和△BAH中，
∴△ADF≌△BAH（ASA），
∴DF＝AH，AF＝BH，
故选项B正确；
∵∠FAP＝30°，AH⊥CD，
∴AF＝2PF，
∴BH＝2PF，
故选项C正确；
∵∠AFG＝∠CBG＝60°，∠AGF＝∠CGB，
∴△AFG∽△CBG，
AGFG=CGBG
∵2CG＝3BG，
∴2AG＝3FG，
故选项D不正确，
故答案为：D
【分析】根据等边三角形的性质以及等腰直角三角形的性质可得△CAD是等腰三角形，∠CAD＝150°，求解可知A正确；由等腰直角三角形的性质以及三线合一定理得出∠DAE＝45°，由三角形的内角和可求出∠BAH＝∠ADF，通过证明△ADF≌△BAH即可得到DF＝AH；由△ADF≌△BAH可知BH＝AF，再结合求出的∠PAF＝30°，可知AF＝BH＝2PF；通过证明△AFG∽△CBG可得AGFG=CGBG，最后得出2AG＝3FG．
8．【答案】B
【知识点】矩形的性质；相似三角形的应用
【解析】【解答】解：如图：当最上层的小长方形的一边与AB、AC交于点E、F时，EF∥BC，AD⊥BC于D，交EF于G，
∴△AEF∽△ABC，
∴EFBC=AGAD，即520=AG16，
解得，AG=4，
∴DG=AD−AG=12，
∵小长方形的宽为4cm
∴△ABC能分割三层小长方形，且最上一层正好能分割一个小长方形，
设第二层靠近点A的边为x，
根据三角形相似可得：x20=816，
解得x=10，即第二层正好能分割两个小长方形，
设最下层靠近点A的边为y，
根据三角形相似可得：y20=1216，
解得y=15，即最下层正好能分割三个小长方形，
∴按如图方式分割成的小长方形零件最多有1+2+3=6个，
故答案为：B.
【分析】 当最上层的小长方形的一边与AB、AC交于点E、F时，EF∥BC，AD⊥BC于D，交EF于G，则△AEF∽△ABC，由相似三角形对应边成比例建立方程可求出AG的长，然后根据DG=AD-AG可求出DG的长， 所以△ABC能分割三层小长方形，且最上一层正好能分割一个小长方形，设第二层靠近点A的边为x，根据相似三角形对应边成比例建立方程求出x=10，即第二层正好能分割两个小长方形，设最下层靠近点A的边为y，根据相似三角形对应边成比例建立方程求出y=15，即最下层正好能分割三个小长方形，从而即可得出答案.
9．【答案】4
【知识点】相似三角形的应用
【解析】【解答】解：由题意可得，CE∥BD，
∴△ACE∼△ABD
∴ACAB=CEBD
即13+1=1BD
解得BD=4米，
故答案为：4.
【分析】由题意可得，CE∥BD，由平行于三角形一边的直线截其它两边，所截的三角形与原三角形相似得△ACE∽△ABD，进而根据相似三角形对应边成比例建立方程可求出BD.
10．【答案】5
【知识点】平行线分线段成比例；相似三角形的应用
【解析】【解答】解：∵AB∥CD，
∴OAOC=ABCD，
∴3010=15CD，
∴CD=5cm.
故答案为：5.
【分析】根据平行线分线段成比例定理得出OAOC=ABCD，代入数值进行计算，即可得出答案.
11．【答案】5
【知识点】相似三角形的应用
【解析】【解答】解：根据题意，易得△MBA∽△MCO，
根据相似三角形的性质可知ABOC=AMOA+AM，即1.68=AM20+AM，解得AM=5．
∴小明的影长为5米．
【分析】先求出1.68=AM20+AM，再计算求解即可。
12．【答案】AD=4BE
【知识点】相似三角形的性质；相似三角形的应用
【解析】【解答】解：由题意可得：AB=AD=BD，BO=12BD
在△OEB和△AOB中，∠OEB=∠AOB，∠OBE=∠ABO
∴△OEB~△AOB
∴OBAB=EBOB
∴EB=OB2AB=12BD2BD=14BD=14AD
∴AD=4BE
故答案为AD=4BE
【分析】利用三角形的相似，根据相似比即可求出答案。
13．【答案】32cm2
【知识点】相似三角形的应用
【解析】【解答】解：由题意得：△ABC~△A'B'C'
∵平面q到平面n的距离是平面n到平面m的距离的2倍
∴ABA'B'=ACA'C'=12
A'B'=2AB=2×4=8，A'C'=2AC=2×4=8
∴△A'B'C' 的面积为：12×8×8=32cm2
故答案为：32cm2
【分析】根据相似三角形的性质，相似三角形的周长的比等于相似比即可得到结论。
14．【答案】解：由题意，BD∥AC．
∴△BDE∽△ACE．
∴BDBE=ACAE．
∴10.2=AC1.8-0.2．
解得AC＝8．
答：井深AC的长为8米．
【知识点】相似三角形的应用
【解析】【分析】先证明△BDE∽△ACE，再利用相似三角形的性质可得BDBE=ACAE，然后将数据代入计算可得AC＝8。
15．【答案】解：过点H作HM⊥AC于点M，交ED于点N，如图所示：
易得NH=DG=3米，MN=CD=33米，
∴MH=MN+HN=36米．
∵AC⊥CG，FD⊥CG，
∴AC∥FD，
∴∠BAH=∠EFH，∠ABH=∠FEH，
∴△ABH∽△FEH，
∴ABFE=EHNH，
同理得：△BHM∽△ENH，
∴BHEH=MHHN，
∴ABFE=MHHN，
即AB1=363，
∴AB=12，
∴人物铜像的高度AB为12米．
【知识点】相似三角形的应用
【解析】【分析】过点H作HM⊥AC于点M，交ED于点N，则NH=DG=3米，MN=CD=33米，MH=MN+HN=36米，由垂直于同一直线的两直线互相平行可得AC∥FD，根据平行线的性质可得∠BAH=∠EFH，∠ABH=∠FEH，利用两角对应相等的两个三角形相似可得△ABH∽△FEH，△BHM∽
△ENH，由相似三角形的性质可求出AB的值，据此解答.
16．【答案】（1）证明：如图所示，连接 OA ，
∵AC 平分 ∠BCD ，
∴∠OCA=∠DCA ，
∵OA=OC ，
∴∠OAC=∠OCA=∠DCA ，
∴OA∥CD ，
∵AD⊥CD ，
∴OA⊥AD ，
又∵OA 是 ⊙O 的半径，
∴AD 是 ⊙O 的切线；
（2）解：∵BC 是直径，
∴∠BAC=90° ，
∵点E是 AB 的中点，点O是 BC 的中点，
∴OE 是 △ABC 的中位线，
∴AC=2OE=6 ，
∵∠CDA=∠CAB=90°，∠ACD=∠BCA ，
∴△CAB∽△CDA ，
∴CDAC=CABC ，即 CD6=610 ，
∴CD=3.6 ．
【知识点】相似三角形的应用
【解析】【分析】（1）如图所示，连接OA，由角平分线的定义得到∠OCA＝∠DCA，再由等边对等角推出∠OAC＝∠OCA＝∠DCA，则OA∥CD，即可证明OA⊥AD，则AD是⊙O的切线；
（2）先由直径所对的圆周角是直角得到∠BAC＝90°，再证明OE是△ABC的中位线，得到AC＝2OE＝6，进一步证明△CAB∽△CDA，利用相似三角形的性质即可求出CD＝3.6．
17．【答案】（1）解：∵AB∥CD，
∴△OAB∽△OCD，
∴ABCD=OEOF，
∴+EF，
解得EF=80(dm).
（2）解：由（1）得，ABCD=OEOF，
∴0.3y=xx+80，
∴y=0.3+24x或y=0.3x+24x，
性质：当x>0时，y随x的增大而减小.
(注：写出其他性质，只要合理均可给分)
（3）解：由y≥3，0.3+24x≥3，
则0.3x+24≥3x，
解得x≤809，
∴OE的取值范围为：0