（期末押题卷）2023-2024学年五年级数学上册期末考试高频易错题押题检测卷二（人教版）

这是一份（期末押题卷）2023-2024学年五年级数学上册期末考试高频易错题押题检测卷二（人教版），共7页。试卷主要包含了点A的位置是，盒子里装有7个红球，3个黄球等内容，欢迎下载使用。

考试分数：100分；考试时间：90分钟
注意事项：
1．答题前，填写好自己的姓名、班级、考号等信息，请写在答题卡规定的位置上。
2．选择题、判断题必须使用2B铅笔填涂答案，非选择、判断题必须使用黑色墨迹签字笔或钢笔答题，请将答案填写在答题卡规定的位置上。
3．所有题目必须在答题卡上作答，在试卷上作答无效。
4．考试结束后将试卷和答题卡一并交回。
一、选择题（共16分）
1．下面简便计算方法不正确的是（ ）。
A．9.9×4.7＝（10－0.1）×4.7B．3.5×2.5＋5×0.25＝（3.5＋0.5）×2.5
C．1.25×7.8×0.8＝1.25×0.8×7.8D．5.46×100.1＝5.46×100＋5.46×1
2．在周长900米的环湖小路边，每隔100米安装一个采集图像的摄像头，一共需要安装（ ）个。
A．8B．9C．10D．11
3．盒子里有大小、形状相同的白球、黑球共16个，如果任意摸一个球，摸到白球的可能性大，则白球至少要有（ ）个。
A．7B．8C．9D．15
4．下面的式子中，（ ）不是方程。
A．B．C．D．
5．一个三角形的底是，如果底增加，那么三角形的面积就增加，原来三角形的面积是（ ）。
A．0.2B．3.6C．4.8D．7.2
6．点A的位置是（5，3），点B的位置是（7，6），点C与点A在同一列，与点B在同一行，则点C的位置是（ ）。
A．（5，6）B．（3，7）C．（5，7）D．（7，3）
7．某工厂要运送一批50吨的货物，2小时运走了12.5吨，还要多少小时才能把剩下的全部运走？下列思考过程正确的有（ ）个。
① ②
③ ④
A．1B．2C．3D．4
8．下面算式的商与42÷13的商不相等的是（ ）。
A．0.42÷0.13B．0.42÷1.3C．420÷130D．4.2÷1.3
二、填空题（共16分）
9．盒子里装有7个红球，3个黄球。从盒子里任意摸出一个球，摸到红球的可能性 ( )，摸到黄球的可能性( )，( )摸到白球。
10．工人叔叔沿着一条街道的两边安装路灯，每隔50米安一盏（两端都要安装），共安装了80盏，这条街道长( )千米。
11．在一个面积是48平方厘米的平行四边形里剪一个最大的三角形，这个三角形的面积是( )平方厘米。
12．明明的座位在第六排第三个位置，用数对表示他的位置是（3，6），他前一个同学露露的位置用数对表示是( )。
13．李叔叔1.5小时做30个零件，平均每小时做( )个零件，每个零件需要( )小时。
14．任意翻一下日历，( )翻出11月15日，( )翻出11月31日。（填“可能”或“不可能”）
15．一本书a页，小明每天看页，看了4天，还剩( )页没看；当a＝128，＝18时，还剩( )页。
16．13.56×4＋6×13.56可以用( )律进行简算。0.25×3.5×4可以用( )律进行简算。
三、判断题（共8分）
17．数对（2,5）和数对（6,5）在同一行上． ( )
18．0.4×8×2.5×8＝8×（0.4×2.5）。 ( )
19．袋子里面装有白球和黑球，随机摸出1个，摸出白球的可能性大，说明袋子里白球装得多． ( )
20．等底等高的两个三角形面积一定相等。( )
四、计算题（共18分）
21．（6分）列竖式计算。
10.75÷12.5＝ 3.25×9.04＝ （计算并验算）
289.8÷0.18＝ 6.5×2.16＝
22．（6分）解方程。
0.4÷0.5＝8.8 2.4＋0.7＝8.37 6＋1.8×7＝23.4
23．（6分）求下列图形的面积。（单位：m）

五、作图题（共6分）
24．（6分）
（1）在下图中标出下列各场所的位置。
学校（5，3） 商场（6，7）
（2）上周六，玲玲的活动路线是（8，1）→（8，5）→（2，4）→（5，2）→（8，1）。请将她的活动路线画出来。
六、解答题（共36分）
25．（6分）在一块平行四边形的草坪中铺了一条宽为1米的小路，每平方米的草坪需要50元，求铺这块草坪需要多少元？
26．（6分）小勇登山，从山脚到山顶有8.4千米，他上山用了3小时，下山用了2小时，他从上山到下山的平均速度是多少？
27．（6分）两列火车从相距550km的两地同时相向开出。甲车每小时行120km，乙车每小时行100km，经过几小时两车相遇？（先写出数量关系式，再列方程解答）
数量关系式：_____________。
列方程解答：_____________。
28．（6分）要铺设一条长1500米的污水管道。甲施工队单独铺设需要10天，乙施工队单独铺设需要8天，如果两个施工队合作铺设4天后，还剩下多少米没有铺设完成？
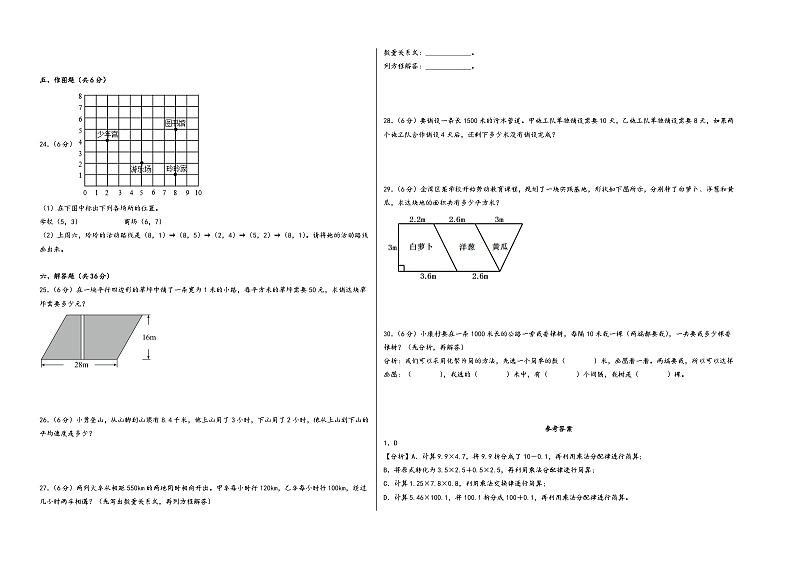
29．（6分）金湾区某学校开始劳动教育课程，规划了一块实践基地，形状如下图所示，分别种了白萝卜、洋葱和黄瓜，求这块地的面积共有多少平方米？
30．（6分）小康村要在一条1000米长的公路一旁栽香樟树，每隔10米栽一棵（两端都要栽），一共要栽多少棵香樟树？（先分析，再解答）
分析：我们可以采用化繁为简的方法，先选一个简单的数（ ）米，画图看一看。两端要栽，所以可以这样画图：（ ），我选的（ ）米中，有（ ）个间隔，栽树是（ ）棵。
参考答案
1．D
【分析】A．计算9.9×4.7，将9.9拆分成了10－0.1，再利用乘法分配律进行简算；
B．将原式转化为3.5×2.5＋0.5×2.5，再利用乘法分配律进行简算；
C．计算1.25×7.8×0.8，利用乘法交换律进行简算；
D．计算5.46×100.1，将100.1拆分成100＋0.1，再利用乘法分配律进行简算。
【详解】A．9.9×4.7＝（10－0.1）×4.7，正确；
B．3.5×2.5＋5×0.25＝（3.5＋0.5）×2.5，正确；
C．1.25×7.8×0.8＝1.25×0.8×7.8，正确；
D．5.46×100.1＝5.46×100＋5.46×0.1，原题错误；
故答案为：D。
整数乘法运算律在小数乘法中同样适用。
2．B
【分析】把环湖小路看作一个封闭图形，所以植树棵数＝间隔数，所以用周长除以间距即可。
【详解】900÷100＝9（个）
故答案为：B。
在封闭线路上植树，棵数与段数相等，即：棵数＝间隔数。
3．C
【分析】可能性的大小与球数量的多少有关，数量多则被摸到的可能性较大，反之，则可能性就小，据此解答即可。
【详解】16÷2＋1
＝8＋1
＝9（个）
所以白球至少要有9个。
故答案为：C
本题考查可能性，明确可能性的大小与数量的多少有关是解题的关键。
4．A
【分析】含有未知数的等式是方程，据此解答即可。
【详解】A．不是等式，所以不是方程；
B．4＋x＝5，是方程；
C．0.6y＝6，是方程；
D．m÷7＝3，是方程。
故答案为：A
本题考查方程的意义，解答本题的关键是掌握方程的意义。
5．B
【分析】一个三角形的底是3cm ，如果底增加1cm ，那么三角形的面积就增加1.2cm2 ，高不变；增加的面积就是底为1厘米的的三角形，根据三角形面积公式求出高，再求出原来三角形面积即可。
【详解】3×（1.2×2÷1）÷2
＝3×2.4÷2
＝7.2÷2
＝3.6（cm2）
故答案为：B
本题考查三角形的面积，解答本题的关键是掌握三角形的面积公式。
6．A
【分析】用数对表示位置时，前一个数表示第几列，后一个数表示第几行；据此可知，（5，3）表示第5列第3行，（7，6）表示第7列第6行，已知点C与点A在同一列，与点B在同一行，说明C在第5列第6行，所以C用数对表示为（5，6）。
【详解】点A的位置是（5，3），点B的位置是（7，6），点C与点A在同一列，与点B在同一行，则点C的位置是（5，6）。
故答案为：A
7．C
【分析】根据计算步骤，逐项进行分析，再进行选择即可。
【详解】①50÷（12.5÷2），（12.5÷2）求出每小时运走的货物，进而求出一共需要的总时间；不符合题意；
②（50－12.5）÷12.5×2，（50－12.5）求出剩下的货物数量，用剩下的货物数量除以12.5，就是求剩下的货物里有几个12.5吨，进而求出的是运走剩下的货物需要的时间；符合题意；
③50÷（12.5÷2）－2，（12.5÷2）求出每小时运走的货物，再利用货物的总数除以每小时运走的数量即可求出需要的总时间，再减去原来的已经运了时间，符合题意；
④（50－12.5）÷（12.5÷2），（50－12.5）求出剩下的货物数量，再用（12.5÷2）求出每小时运走的货物，进而求出运走剩下的货物需要的时间，符合题意；
所以，有②、③和④满足题意。
故答案为：C
8．B
【分析】商不变的性质：被除数和除数同时乘或除以相同的数（0除外），商不变。根据商不变的性质选择即可。
【详解】A．因为除数0.13是两位小数，所以根据商不变的性质，被除数和除数同时除以100，即42÷13＝（42÷100）÷（13÷100）＝0.42÷0.13。所以42÷13与0.42÷0.13的商相等。
B．因为除数1.3是一位小数，所以根据商不变的性质，被除数和除数同时除以10，即42÷13＝（42÷10）÷（13÷10）＝4.2÷1.3。所以42÷13与0.42÷1.3的商不相等。
C．因为除数130，所以根据商不变的性质，被除数和除数同时乘10，即42÷13＝（42×10）÷（13×10）＝420÷130。所以42÷13与420÷130的商相等。
D．因为除数1.3是一位小数，所以根据商不变的性质，被除数和除数同时除以10，即42÷13＝（42÷10）÷（13÷10）＝4.2÷1.3。所以42÷13与4.2÷1.3的商相等。
故答案为：B
9． 大 小 不可能
【分析】根据可能性大小的判断方法，比较盒子里红球、黄球的数量多少，数量多的，摸到的可能性大；反之，数量最少的，摸到的可能性就小。
盒子如果没有哪种颜色的球，那么不可能摸到这种颜色的球。
【详解】7＞3
红球的数量多，黄球的数量少，没有白球；
所以从盒子里任意摸出一个球，摸到红球的可能性大，摸到黄球的可能性小，不可能摸到白球。
10．1.95
【分析】本题考查两端都栽的植树问题。沿着一条街道的两边安装路灯，每隔50米安一盏，一共安装了80盏，则一边安装80÷2＝40（盏），两端都安装，那么间隔数就是40一1＝39（个），间隔距离是50米，所以这条街道长39×50＝1950（米），1950米＝1.95千米。据此解答。
【详解】80÷2＝40（盏）
（40一1）×50
＝39×50
＝1950（米）
1950米＝1.95千米
这条街道长1.95千米。
本题考查两端都栽的植树问题。理解“两端都安装路灯，间隔数用灯盏数减1”是解答的关键。
11．24
【分析】每个平行四边形都可以沿对角线剪成两个三角形，这两个三角形可以重合，且是这个平行四边形内可以剪成的面积最大的三角形。据此解题即可。
【详解】48÷2＝24平方厘米
所以，在这个平行四边形内可以剪成的最大三角形的面积是24平方厘米。
本题考查了平行四边形和三角形的关系，明确每个平行四边形都是由两个完全一致的三角形组成的，是解题的关键。
12．（3，5）
【分析】根据明明的位置可知，数对的第一个数表示顺序，第二个数表示排数，他前一个同学的位置顺序一样，排数减1，据此分析。
【详解】明明的座位在第六排第三个位置，用数对表示他的位置是（3，6），他前一个同学露露的位置用数对表示是（3，5）。
13． 20 0.05
【分析】用做零件的数量÷做零件的时间，即用30÷1.5，即可求出平均每小时做零件的个数；
用做零件的时间÷做零件的个数，即可求出每个零件需要的时间。
【详解】30÷1.5＝20（个）
1.5÷30＝0.05（小时）
李叔叔1.5小时做30个零件，平均每小时做20个零件，每个零件需要0.05小时。
14． 可能 不可能
【分析】根据事件发生的确定性和不确定性进行分析：任意翻一下日历，可能翻出11月15日，因为有11月15日这一天，不可能翻出11月31日，因为11月只有30天；由此解答即可。
【详解】由分析可知：
任意翻一下日历，可能翻出11月15日，不可能翻出11月31日。
15． a－4 56
【分析】根据题意可得出数量关系：总页数－每天看的页数×看的天数＝剩下的页数，据此用含字母的式子表示还剩的页数；
然后把a＝128，＝18代入式子中，计算出得数即可。
【详解】还剩：a－×4＝（a－4）页
当a＝128，＝18时
a－4
＝128－4×18
＝128－72
＝56（页）
一本书a页，小明每天看页，看了4天，还剩（a－4）页没看；当a＝128，＝18时，还剩56页。
16． 乘法分配 乘法交换
【分析】乘法分配律：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，反过来运用也可以。
乘法交换律：两个数相乘，交换两个因数的位置，积不变。
【详解】13.56×4＋6×13.56＝13.56×（4＋6），可以用乘法分配律进行简算。
0.25×3.5×4＝0.25×4×3.5，可以用乘法交换律进行简算。
整数的运算定律同样适用于小数。
17．√
【详解】略
18．×
【分析】分别计算两边的结果，然后再比较比较即可。
【详解】0.4×8×2.5×8
＝（0.4×8）×（2.5×8）
＝3.2×20
＝64
8×（0.4×2.5）
＝8×1
＝8
64≠8
所以0.4×8×2.5×8≠8×（0.4×2.5）。原题干说法错误。
故答案为：×
本题考查了小数乘法运算律的应用，明确整数的运算律在小数同样适用。
19．√
【详解】袋子里面装有白球和黑球，随机摸出1个，哪种颜色球的个数多，摸出的可能性就大．摸出白球的可能性大，说明袋子里白球装得多；摸出黑球的可能性大，说明袋子里黑球装得多．
20．√
【分析】三角形面积的大小与三角形的底和高有关，当两个三角形的底和高都相等时，那么这两个三角形的面积相等。
【详解】三角形的面积＝底×高÷2，由三角形的面积公式可知，等底等高的两个三角形面积一定相等。
故答案为：√
掌握三角形的面积计算公式是解答题目的关键。
21．0.86；29.38
1610；14.04
【分析】除数是小数的小数除法，先移动除数的小数点，使它变成整数；除数的小数点向右移动几位，被除数的小数点也向右移动几位（位数不够的，在被除数的末尾用0补足）；然后按除数是整数的小数除法进行计算。
小数乘法先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点；如果小数的位数不够，需要在前面补0占位。
【详解】10.75÷12.5＝0.86 3.25×9.04＝29.38
验算：
289.8÷0.18＝1610 6.5×2.16＝14.04

22．＝11；＝2.7；＝1.8
【分析】根据等式的性质解方程。
（1）先把方程化简成0.8＝8.8，然后方程两边同时除以0.8，求出方程的解；
（2）先把方程化简成3.1＝8.37，然后方程两边同时除以3.1，求出方程的解；
（3）先把方程化简成6＋12.6＝23.4，然后方程两边先同时减去12.6，再同时除以6，求出方程的解。
【详解】（1）0.4÷0.5＝8.8
解：0.8＝8.8
0.8÷0.8＝8.8÷0.8
＝11
（2）2.4＋0.7＝8.37
解：3.1＝8.37
3.1÷3.1＝8.37÷3.1
＝2.7
（3）6＋1.8×7＝23.4
解：6＋12.6＝23.4
6＋12.6－12.6＝23.4－12.6
6＝10.8
6÷6＝10.8÷6
＝1.8
23．9.9m2；60m2；168m2
【分析】（1）根据三角形的面积＝底×高÷2，代入数据计算求解；
（2）根据平行四边形的面积＝底×高，代入数据计算求解；
（3）如下图，图形的面积＝长方形的面积＋梯形的面积，根据长方形的面积＝长×宽，梯形的面积＝（上底＋下底）×高÷2，代入数据计算求解。

【详解】（1）4.5×4.4÷2
＝19.8÷2
＝9.9（m2）
三角形的面积是9.9m2。
（2）12×5＝60（m2）
平行四边形的面积是60m2。
（3）10×6＋（10＋14）×（15－6）÷2
＝60＋24×9÷2
＝60＋108
＝168（m2）
梯形的面积是168m2。
24．见详解
【分析】（1）数对的第1个数表示列，第2个数表示行，据此标出商场和学校的位置；
（2）根据数对找到位置，并按数对的顺序依次把各点连接起来即可。
【详解】（1）（2）见下图：
本题主要考查学生对用数对表示位置知识的掌握。
25．21600元
【分析】用底边长为28米，高为16米的平行四边形的面积减去长为16米，宽为1米的长方形，分别利用平行四边形和长方形的面积公式求出平行四边形的草坪面积和空地的面积，再用平行四边形的草坪面积减去空地的面积，即是应铺草坪的面积，再乘每平方米的草坪的造价，从而得解。
【详解】28×16－16×1
＝448－16
＝432（平方米）
432×50＝21600（元）
答：铺这块草坪需要21600元。
此题主要考查组合图形的面积，灵活运用平行四边形、长方形的面积公式解决问题。
26．3.36千米/小时
【分析】平均速度＝总路程÷总时间，上山和下山的路程是一样的，总路程是单程的2倍，代入数据解答即可。
【详解】8.4×2÷（3＋2）
＝16.8÷5
＝3.36（千米/时）
答：他从上山到下山的平均速度是3.36千米/时。
此题考查小数乘除法的计算以及平均速度的求法。
27．（甲车速度＋乙车速度）×相遇时间＝两地距离550km；
（120＋100）x＝550，x＝2.5
【分析】两车相遇时，两车的路程和恰好等于两地的距离，据此填出数量关系式。再根据数量关系式，列方程解方程即可。
【详解】数量关系式：（甲车速度＋乙车速度）×相遇时间＝两地距离550km
解：设经过x小时两车相遇。
（120＋100）x＝550
220x＝550
x＝550÷220
x＝2.5
答：经过2.5小时两车相遇。
本题考查了相遇问题，两车同时相对而行，相遇时的路程和等于两地的距离。
28．150米
【分析】根据工作总量÷工作时间＝工作效率，即用1500除以10即可得到甲施工队的工作效率，用1500除以8即可得到乙施工队的工作效率，再根据工作效率之和×工作时间＝工作总量，据此求出两个施工队合作铺设4天可完成铺设的长度，最后用污水管道的总长度减去已经完成铺设的长度即可求出还剩下多少米没有铺设完成。
【详解】1500÷10＝150（米）
1500÷8＝187.5（米）
（150＋187.5）×4
＝337.5×4
＝1350（米）
1500－1350＝150（米）
答：还剩下150米没有铺设完成。
29．21平方米
【分析】这块地的形状是梯形，梯形的上底是（3.6＋2.6）米，梯形的下底是（2.2＋2.6＋3）米，梯形的高是3米。梯形的面积＝（上底＋下底）×高÷2，把梯形上底、下底、高的数值代入公式计算即可求出这块地的面积。
【详解】上底：3.6＋2.6＝6.2（米）
下底：2.2＋2.6＋3
＝4.8＋3
＝7.8（米）
面积：（6.2＋7.8）×3÷2
＝14×3÷2
＝42÷2
＝21（平方米）
答：这块地的面积共有21平方米。
此题主要考查了梯形面积计算公式的应用。计算梯形的面积时，不要忘记除以2。
30．100；画图见详解；100；10；11
101棵
【分析】根据对植树问题的总结：
如果植树线路的两端都植树，那么全长÷间距＝间隔数，用间隔数再加上1就是植树棵数；
如果植树线路的两端都不植树，那么全长÷间距＝间隔数，用间隔数再减去1就是植树棵数；
如果植树线路的一端植树，另外一端不植树，那么全长÷间距＝间隔数，间隔数等于植树棵数，据此判断即可。
【详解】由分析可得：
我们可以采用化繁为简的方法，先选一个简单的数100米，画图如下：
由图可见，我选中的100米中，有10个间隔，栽树是11棵。
1000÷10＋1
＝100＋1
＝101（棵）
答：一共要栽101棵香樟树。
本题考查了植树问题的相关知识，注意按情况讨论，不同的植树方式有不同的间隔数和不同的棵数。