黑龙江省齐齐哈尔市建华区2023-2024学年九年级上学期期末数学试题

这是一份黑龙江省齐齐哈尔市建华区2023-2024学年九年级上学期期末数学试题，共9页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
一、单项选择题（每小题3分，满分30分）
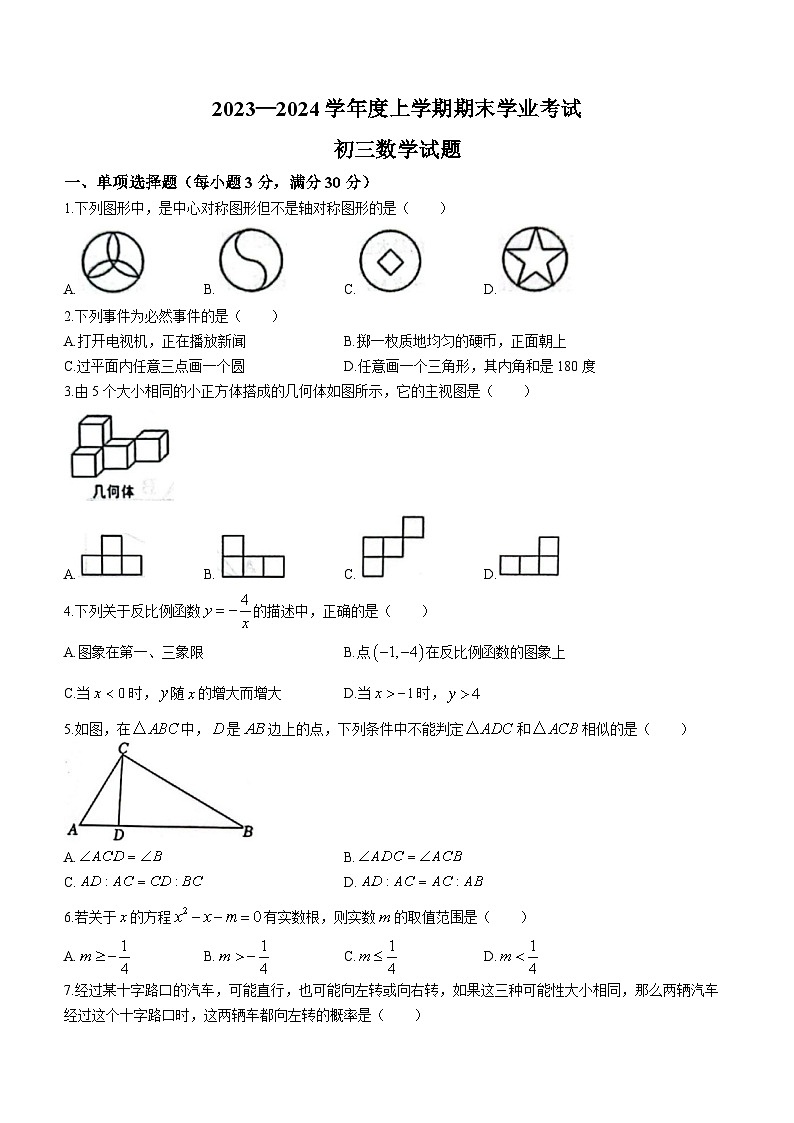
1.下列图形中，是中心对称图形但不是轴对称图形的是（ ）
A.B.C.D.
2.下列事件为必然事件的是（ ）
A.打开电视机，正在播放新闻B.掷一枚质地均匀的硬币，正面朝上
C.过平面内任意三点画一个圆D.任意画一个三角形，其内角和是180度
3.由5个大小相同的小正方体搭成的几何体如图所示，它的主视图是（ ）
A.B.C.D.
4.下列关于反比例函数的描述中，正确的是（ ）
A.图象在第一、三象限B.点在反比例函数的图象上
C.当时，随的增大而增大D.当时，
5.如图，在中，是边上的点，下列条件中不能判定和相似的是（ ）
A.B.
C.D.
6.若关于的方程有实数根，则实数的取值范围是（ ）
A.B.C.D.
7.经过某十字路口的汽车，可能直行，也可能向左转或向右转，如果这三种可能性大小相同，那么两辆汽车经过这个十字路口时，这两辆车都向左转的概率是（ ）
A.B.C.D.
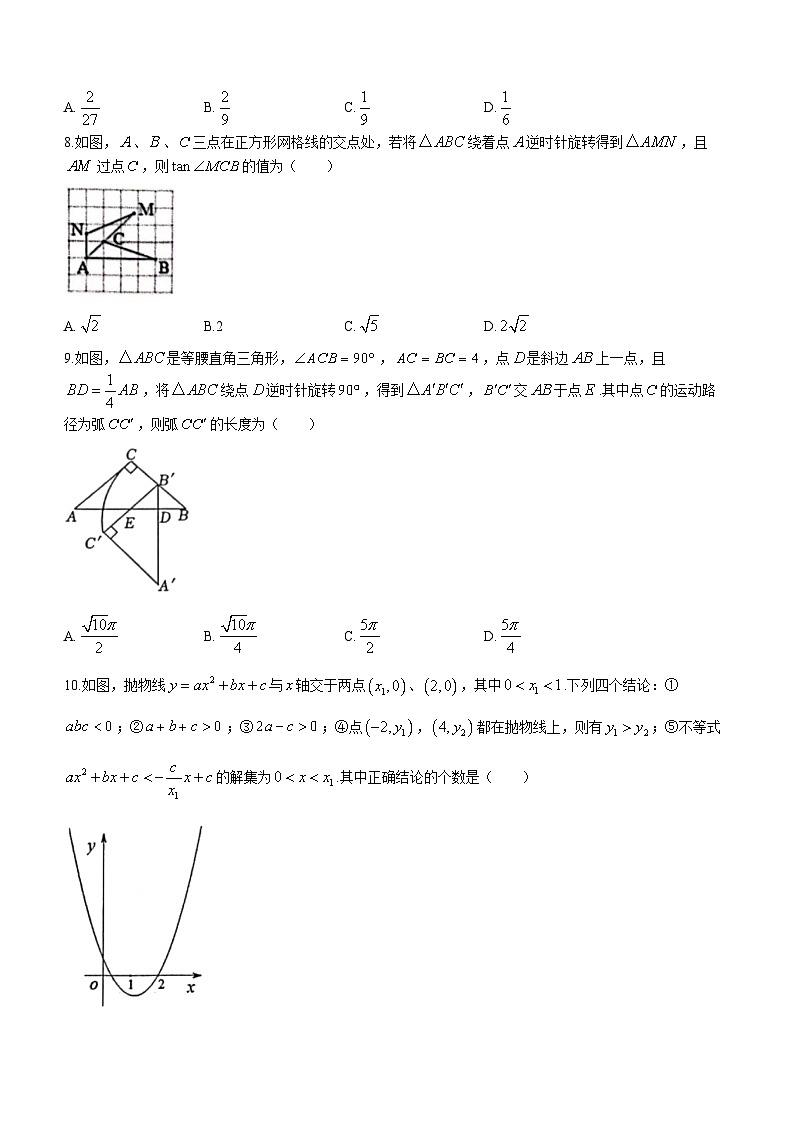
8.如图，、、三点在正方形网格线的交点处，若将绕着点逆时针旋转得到，且过点，则的值为（ ）
A.B.2C.D.
9.如图，是等腰直角三角形，，，点是斜边上一点，且，将绕点逆时针旋转，得到，交于点.其中点的运动路径为弧，则弧的长度为（ ）
A.B.C.D.
10.如图，抛物线与轴交于两点、，其中.下列四个结论：①；②；③；④点，都在抛物线上，则有；⑤不等式的解集为.其中正确结论的个数是（ ）
A.1B.2C.3D.4
二、填空题（每小题3分，满分21分）
11.若，则________.
12.已知圆锥的底面半径为5，高为12，则它的侧面展开图的面积是________.
13.一个不透明的箱子中有5个红球和若干个黄球，除颜色外无其它差别.若任意摸出一个球，摸出红球的概率为，则这个箱子中黄球的个数为________个.
14.如图所示的衣架可以近似看成一个等腰三角形，其中，，，则高为________.
15.如图，矩形的两边、分别在平面直角坐标系的坐标轴上，点的坐标为，点为中点，反比例函数的图象经过点，交于点，连接、、，则的面积为________.
16.在矩形中，，，点是边上一点，将沿折叠，使点的对应点落在矩形的对称轴上，则此时________.
17.如图，在平面直角坐标系中，的顶点在直线：上，顶点在轴上，垂直轴，且，顶点在直线：上，；过点作直线的垂线，垂足为，交轴于，过点作垂直轴，交于点，连接，得到第一个；过点作直线的垂线，垂足为，交轴于，过点作垂直轴，交于点，连接，得到第二个；如此下去，…，则的面积是________.
三、解答题（本题共6道大题，共69分）
18.（本题共2个小题，（1）小题6分，（2）小题5分，共11分）
（1）计算：；
（2）解方程：.
19.（本题满分10分）
如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象相交于点，两点.
（1）分别求出一次函数和反比例函数的解析式；
（2）若点在轴上，位于原点右侧，且，则________.
（3）根据图象，请你直接写出满足条件：的的取值范围.
20.（本题满分10分）
如图，在菱形中，与交于点，于点，交于点.
（1）图中与相似的三角形有________个；
（2）若，，求的长.
21.（本题满分12分）
如图，在中，，以为直径的交于点，连接，过点作，垂足为点，、的延长线交于点.
（1）求证：是的切线；
（2）若，，求的长.
22.（本题满分12分）
在综合实践课上，王老师组织同学们以“图形的旋转”“图形的折叠”为主题开展数学活动.下面是同学们进行相关问题的研究.
在中，.点为线段上一动点（不与、重合），以为顶点作，射线交线段于点，将射线绕点顺时针旋转交射线于点，连接.
【特例感知】如图①，当时，可知：________；
【类比探究】如图②，当，时，
图① 图②
（1）猜想：________，________；
（2）求证：；
（3）【问题探究】当为直角三角形时，________；
（4）【拓展探究】点关于射线的对称点为，线段长度的最小值为________.
23.（本题满分14分）
如图，抛物线与轴交于点、，与轴交于点.点是该抛物线上位于第二象限的动点，连接，.
（1）求抛物线的函数解析式；
（2）当时，求点的横坐标；
（3）点到直线的距离的最大值为________，此时点的坐标为________；
（4）在抛物线的对称轴上找一点，抛物线上找一点，使以点、、、为顶点的四边形为平行四边形，请直接写出点的坐标.
2023-2024学年度上学期期末学业考试（2023.12）
初三数学试题参考答案及评分标准
一、1.B 2.D 3.B 4.C 5.C 6.A 7.C 8.B 9.A 10.D
二、11. 12. 13.15 14. 15.9
16.或 17.
三、18.（1）解：原式………………………………6分
（2），……………………………………5分
19.解：（1）∵反比例函数图象与一次函数图象相交于点，.
∴，解得，∴反比例函数解析式为，
∴，
∴点的坐标为，
∴一次函数解析式为；……………………………………6分
（2）.…………………………………………2分
（3）或.…………………………………………2分
20.解：（1）6………………………………………………2分
（2）在菱形中，
∵，∴，∴
又∵，，∴，，
∵，∴
∴，∴
∴，即，解得，；………………………………8分
21.证明：（1）如图，连接，
∵，∴
又∵，∴
∴
∴，
又∵，
∴
∴，
又∵是半径，
∴是的切线；…………………………………………………………6分
（2）∵，，∴，
∵，∴，
，，
∵，∴，∴
∴.………………………………………………………………6分
22.【特例感知】；……………………………………1分
【类比探究】（1）猜想：、90；…………………………2分
（2）证明：∵，∴，∴，
∵，∴，
∵，∴，
∴；∴……………………………………5分
【问题探究】；…………………………………………2分
【拓展探究】线段长度的最小值为2.……………………………………2分
23.解：（1）∵抛物线与轴交于，，与轴交于.
∴，解得：，∴抛物线的解析式为；………………4分
（2）过点作于，交直线于点，
设直线的解析式为，
则，解得：，∴直线的解析式为.
设点的坐标为为，且
则点的坐标为，
∴，
当时，
解得：
∴点的横坐标为或………………………………5分
（3）点到直线的距离的最大值，此时点的坐标为；………………2分
（4），，.……………………………………3分
（注：以上各题用不同于本参考答案的解法做正确的相应给分）