福建省泉州市培元中学2023-2024学年七年级上学期期中考试数学试卷（含解析）

这是一份福建省泉州市培元中学2023-2024学年七年级上学期期中考试数学试卷（含解析），共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．的相反数是（ ）
A．5B．C．D．
2．下列所画的数轴正确的是（ ）
A． B．
C． D．
3．数字用科学记数法表示为（ ）
A．B．C．D．
4．下列各式中，符合代数式书写要求的是（ ）．
A．B．C．D．
5．光盘的质量标准中规定：厚度为的光盘是合格品，则下列经测量得到的数据中，不合格的是（ ）
A．B．C．D．
6．下列各数，，，，，，其中有理数有（ ）个．
A．2B．3C．4D．5
7．用代数式表示“与的和的平方”，正确的是（ ）
A．B．C．D．
8．下列说法中，错误的个数为（ ）
①平方等于本身的数只有一个；②没有最小的负数，也没有最大的正数；③0既不是正数也不是负数； ④表示的点一定位于原点的左侧．
A．1个B．2个C．3个D．4个
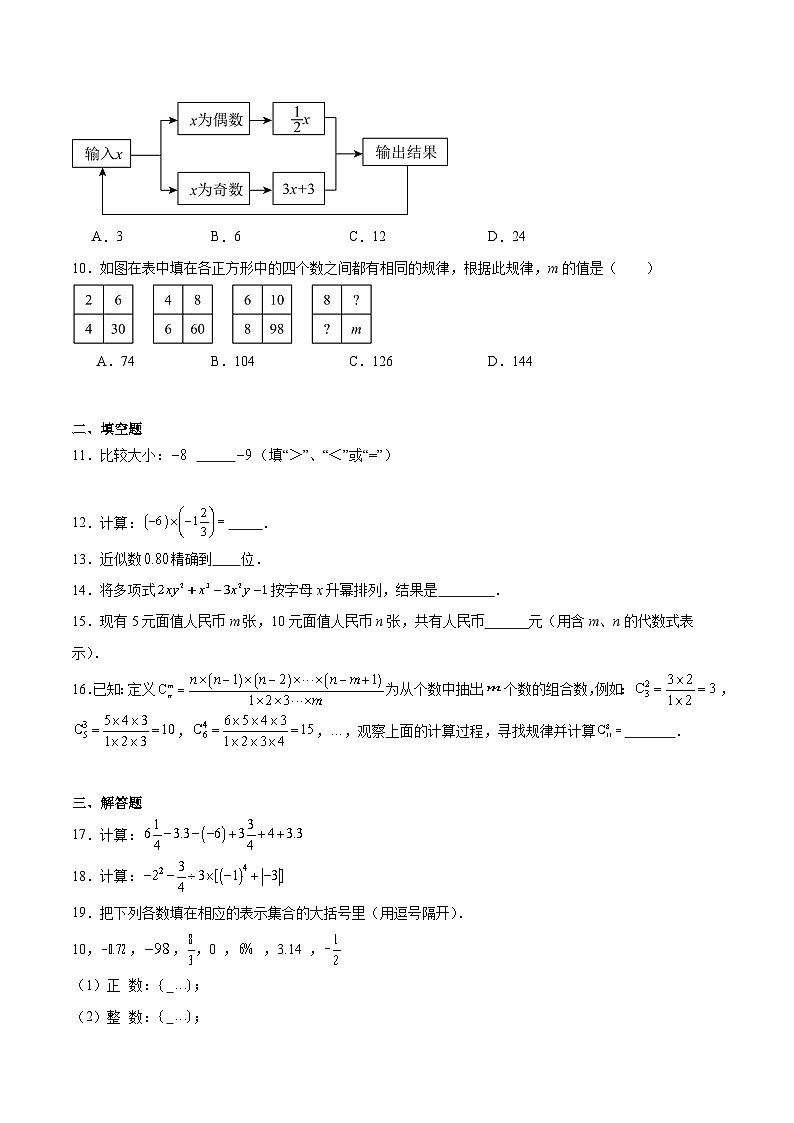
9．如图所示，在这个运算程序当中，若开始输入的x是48，则经过2022次输出的结果是（ ）

A．3B．6C．12D．24
10．如图在表中填在各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（ ）
A．74B．104C．126D．144
二、填空题
11．比较大小： （填“＞”、“＜”或“=”）
12．计算： ．
13．近似数精确到 位．
14．将多项式按字母x升幂排列，结果是 ．
15．现有5元面值人民币m张，10元面值人民币n张，共有人民币 元（用含m、n的代数式表示）．
16．已知：定义为从个数中抽出个数的组合数，例如：，，，…，观察上面的计算过程，寻找规律并计算 ．
三、解答题
17．计算：
18．计算：
19．把下列各数填在相应的表示集合的大括号里（用逗号隔开）．
10，，，，0 ， ，3.14 ，
（1）正 数： ；
（2）整 数： ；
（3）负分数： ；
（4）非负数： ．
20．已知a，b互为相反数，c，d互为倒数，，求：的值．
21．2016年7月，台风“莫利娅”登陆，给我国福建，浙江等省造成严重影响，为民排忧解难的解放军叔叔驾驶冲锋舟沿一条东西方向的河流营救灾民，早晨从A地出发，来回营救灾民，晚上最后到达B地，约定向东为正方向，当天航行依次记录如下（单位：千米）：+16，﹣4，+8，﹣8，+14，﹣7，﹣11．
(1)B地在A地的东面还是西面？与A地相距多少千米？
(2)若冲锋舟每千米耗油0．5升，油箱容量为30升，求途中至少需要补充多少升油？
22．如图所示，将边长为a的小正方形和边长为b的大正方形放在同一水平面上（）．
(1)用a、b表示阴影部分的面积；
(2)计算当，时，阴影部分的面积．
23．任意写出一个三位数（个位，十位，百位上的数字都不为零），任取其三个数字中的两个，组合成所有可能的两位数（有个），求出所有这些两位数的和，然后将它除以原三位数的各个数位上的数字之和．例如，对三位数，取其两个数字组成所有可能的两位数：，，，，，，它们的和是，三位数各位数字的和是，．
(1)若写的三位数是111，最后得到的结果是 ；若写的三位数是345，最后得到的结果是 ；
(2)由（1）的探索过程，若写出的三位数，百位数字是，十位数字是，个位数字是，最后得到的结果是什么？请运用相关知识严格的证明你的猜想．
24．泉州市鲤城区某超市在双十一期间对顾客实行优惠，规定如下：
(1)若张老师一次性购物600元，则她实际付款___________元．
(2)若某顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款_______ 元，当x大于或等于500元时，他实际付款 元（用含x的代数式表示并化简）；
(3)若张老师有两天去超市购物原价合计900元，第一天购物的原价为a元（），请用含a的代数式表示这两天购物张老师的实际付款总额；并求出当元时，张老师两天一共节省了多少元？
25．如图，数轴上有，，三点，其中，两点表示的数分别为，，点位于，两点之间，且满足．
(1)线段的长为 ，点表示的数为 ；
(2)若、、三个动点分别从，，三点同时出发，均沿数轴负方向运动，它们的速度（单位长度/秒）分别是2，，，设运动时间为t秒，求当、、中某两个点重合时，它们与第三个点相距多少个单位长度？
(3)在（2）的条件下，在、、中的某两个点重合时，点立刻改变方向，向数轴正方向移动且保持原速不变．在此后的运动过程中，所形成的三条线段、、，请问是否存在某一时刻t，使得其中一条线段的长度是另一条线段长的4倍？若存在，请你求出时间t的所有可能；若不存在，请说明理由．
参考答案
1．A
解：的相反数是5；
故选A．
2．B
解：A、原点左侧的数据标错，应该是从左到右按照从小到大的顺序排列，本选项不符合题意；
B、正确，本选项符合题意；
C、没有原点，本选项不符合题意；
D、单位长度不一样，本选项不符合题意；
故选：B．
3．B
解：．
故选：B．
4．D
解：应表示为：，故选项A不符合要求；
应表示为：，故选项B不符合要求；
应表示为：，故选项C不符合要求；
的书写规范，故选项D符合题意；
故选：D．
5．D
解：，，
当光盘厚度时，是合格品，
，
的光盘不合格．
故选：D．
6．C
解：，，，，，，
其中有理数有：，，，，共有4个．
故选：C．
7．C
解：与的和的平方表示为：．
故选：C．
8．B
解：①平方等于本身的数有0和1，故①错误；
②没有最小的负数，也没有最大的正数，故②正确；
③0既不是正数也不是负数，故③正确；
④当时，，则表示的点在原点的右边，
当时，，则表示的点在原点，
当时，，则表示的点在原点的左边，故④错误．
综上所述，错误的个数为2．
故选：B．
9．B
解：第一次输入，输出结果为，
第二次输入，输出结果为，
第三次输入，输出结果为，
第四次输入，输出结果为，
第五次输入，输出结果为，
第六次输入，输出结果为，
第七次输入，输出结果为，
第八次输入，输出结果为，
∴推导一般性规律为：从第三次开始，每三次为一个循环，
∴，
∴经过2022次输出的结果是6，
故选：B．
10．D
解析：分析前三个正方形中的数据发现其包含两点规律：（1）从左上到左下到右上是三个连续的偶数；（2）右下的数等于左下的数与右上的数的积加上左上数的3倍.
由此可知.
故选D.
11．＞
解：∵，
∴，
故答案为：＞．
12．10
解析：
．
故答案为：10．
13．百分
解：近似数精确到百分位，
故答案为：百分．
14．
解：将多项式按字母升幂排列：，
故答案为：．
15．
解：由题意得：共有人民币元，
故答案为：
16．165
解：
故填：165．
17．20
解：原式=
=

．
18．
解：原式=
．
19．正数：10，， ，3.14；整数：10，，0 ；负分数：，；非负数：10，，0 ， ，3.14
解：（1）正数： 10，， ，3.14；
（2）整数：10，，0 ；
（3）负分数：，；
（4）非负数：10，，0 ， ，3.14 ．
20．或
解：根据题意得：，，或，
当时，
原式
；
当时，
原式
．
21．（1）∵
∴B地在A地的东面，与A地相距8千米．
（2）∵总路程（千米），
∴（升），
∴途中至少需要补充4升油．
22．（1）解：图中阴影部分的面积：
．
（2）解：当，时，阴影部分的面积为：
=
23．（1）解： ；
；
故答案为：22；22；
（2）猜想：所得结果都是22，理由如下：
设该三位数百位数为，十位数为，个位数为，
则这个三位数可表示为，
组合成的两位数有：，，，，，，
求和得：，
即：；
24．（1）（元），
（2）当x小于500元但不小于200时，实际付款（元），
当x大于或等于500元时，实际付款：（元）
（3）因为第一天购物原价为a元
则第二天购物原价为元，则
第一天购物优惠后实际付款 （元）
第二天购物优惠后实际付款（元）
则一共付款（元）
当元时，实际一共付款（元）
一共节省（元）
答：一共节省了195元．
25．（1）解：；
设点表示的数为，
∵，两点表示的数分别为，，点位于，两点之间，
∴，，
∵，
∴，
解得：，
∴点表示的数为，（如下图）
（2）解：秒时，： ；： ；：；
设经过秒追上，依题意： ，
解得：（秒），
此时相距：
（个单位长度）；
（3）解：由（2）得：第秒时、相遇，且相遇点为：，
此后点开始向数轴正方向移动，即该运动过程中必然满足，
且在此后的运动过程中： ：；
分析可知，反向运动后，、、三点在数轴上恒有：在最左侧，在最右侧，在、之间
∴，
，
，
∵在最左侧，在最右侧，在、之间，且当时，恒成立，
∴ 恒成立，
故若要满足其中一条线段的长度是另一条线段长的倍，可分以下种情况讨论：
①若，
即，
解得：（舍去）；
②若，
即，
解得：；
③若，
即，
解得：（或）；
综上所述：存在值为或时，满足其中一条线段的长度是另一条线段长的倍．一次性购物
优惠办法
少于200元
无优惠
低于500元但不低于200元
全部金额给予8折优惠
500元或超过500元
其中500元部分给予8折优惠，
超过500元部分给予7折优惠