广东省+广州市越秀区育才中学2023-2024学年上学期12月月考九年级+数学试卷

这是一份广东省+广州市越秀区育才中学2023-2024学年上学期12月月考九年级+数学试卷，共8页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
一、单项选择题（每小题3分，共30分）
1．下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（ ）
2．如图，是由绕点顺时针旋转后得到的图形，若点恰好落在上，
且的度数为，则的度数是（ ）
A．B．C．D．
3．已知且对应中线之比为，则与的周长之比为（ ）
A．B．C．D．
4．下列事件为必然事件的是（ ）
A．掷一枚硬币，正面朝上B．位似的两个三角形的对应边互相平行
C．等边三角形的中心角是D．弦是直径
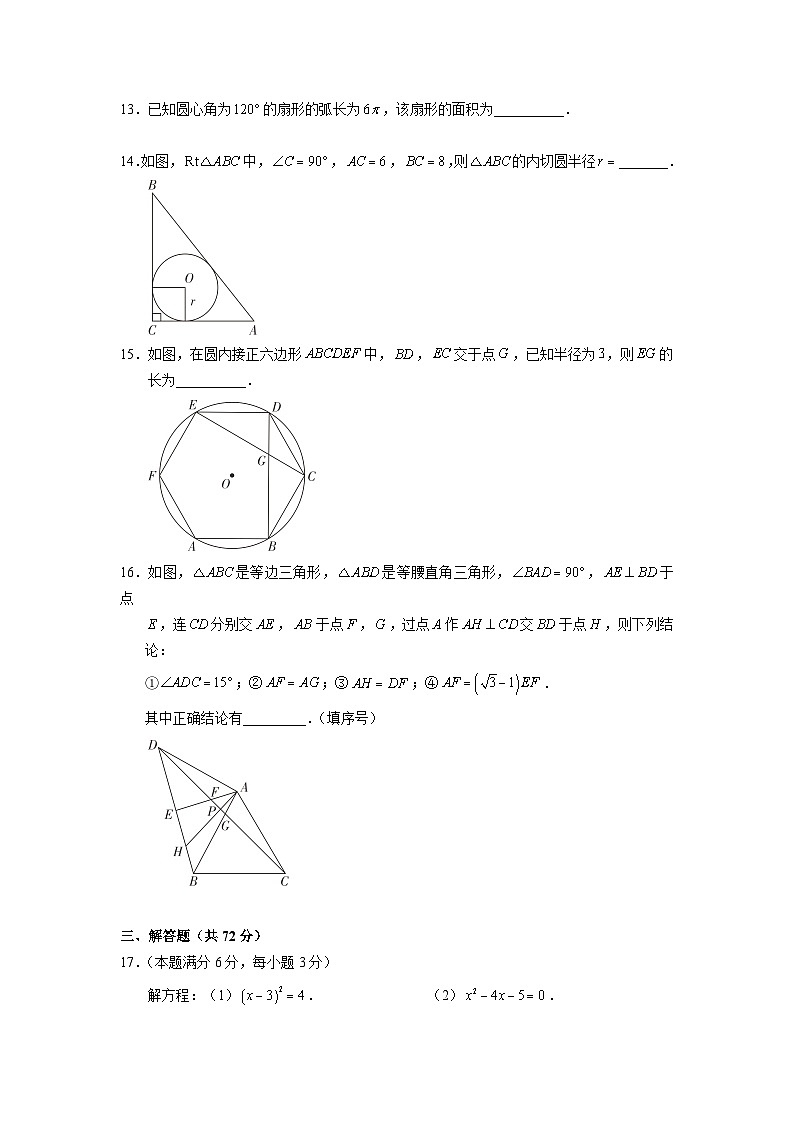
5．现在是流感的高发时期，某校月初有一人患了流感，经过两轮传染后，共人患流感，
假设每轮传染中平均每人传染人，则可列方程（ ）
A．B．
C．D．
6．设，是一元二次方程的两根，则（ ）
A．B．C．D．
7．关于二次函数的图象，下列结论不正确的是（ ）
A．抛物线的开口向上B．当时，随的增大而减小
C．对称轴是直线D．抛物线与轴交于点
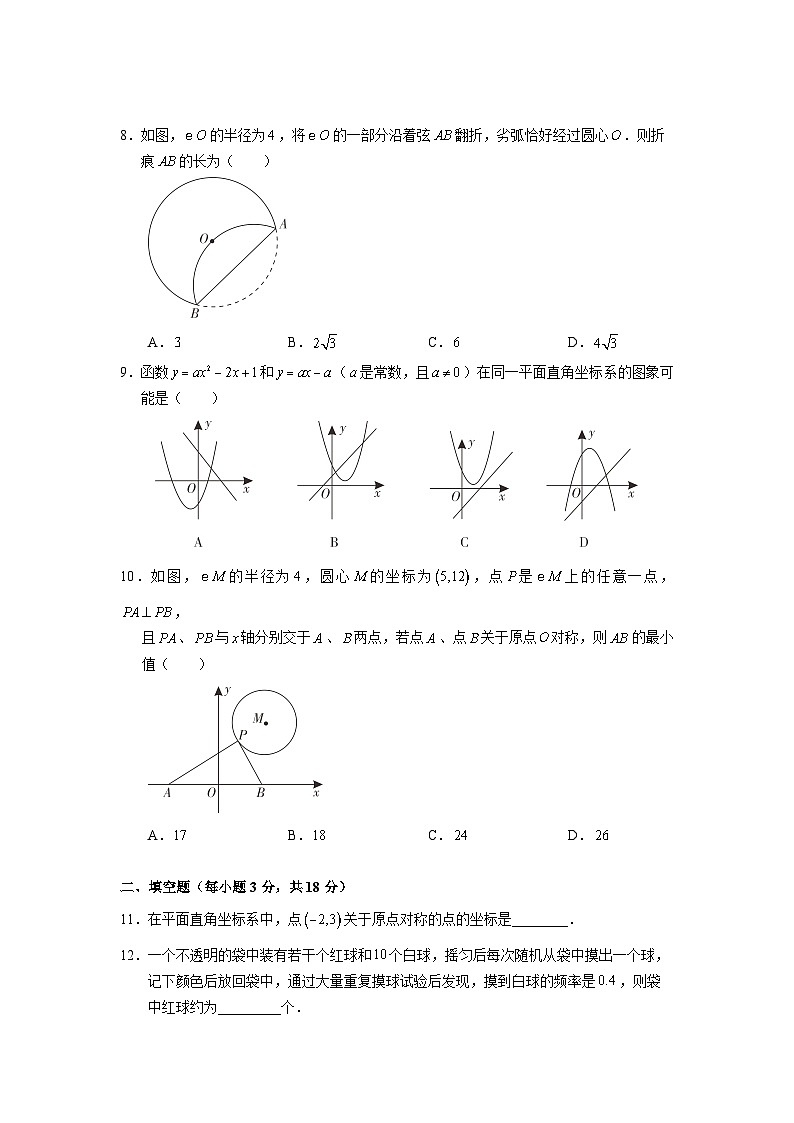
8．如图，的半径为，将的一部分沿着弦翻折，劣弧恰好经过圆心．则折
痕的长为（ ）
A．B．C．D．
9．函数和（是常数，且）在同一平面直角坐标系的图象可能是（ ）
10．如图，的半径为，圆心的坐标为，点是上的任意一点，，
且、与轴分别交于、两点，若点、点关于原点对称，则的最小值（ ）
A．B．C．D．
二、填空题（每小题3分，共18分）
11．在平面直角坐标系中，点关于原点对称的点的坐标是________．
12．一个不透明的袋中装有若干个红球和个白球，摇匀后每次随机从袋中摸出一个球，
记下颜色后放回袋中，通过大量重复摸球试验后发现，摸到白球的频率是，则袋
中红球约为_________个．
13．已知圆心角为的扇形的弧长为，该扇形的面积为__________．
14．如图，中，，，，则的内切圆半径_______．
15．如图，在圆内接正六边形中，，交于点，已知半径为，则的
长为__________．

16．如图，是等边三角形，是等腰直角三角形，，于点
，连分别交，于点，，过点作交于点，则下列结论：
①；②；③；④．
其中正确结论有_________．（填序号）
三、解答题（共72分）
17．（本题满分6分，每小题3分）
解方程：（1）．（2）．
18．（本小题满分4分）
如图，我们想要测量河两岸相对应两点、之间的距离（即河宽），先从点出发与成角方向走到处立一标杆，然后方向不变，继续向前走到处，在处转，沿方向再走到达处，使得、、在同一条直线上，那么河宽是多少米？
19．（本小题满分6分）
如图，已知是坐标原点，、的坐标分别为、
（1）画出绕点顺时针旋转后得到的图形；
（2）在轴的左侧以为位拟中心画出的位似三角形，使新图与原图的相似
比为．
20．（本小题满分6分）
广州的白云山、越秀山、莲花山和大夫山被誉为广州四大名山，不仅风景秀美而且有丰厚的历史底蕴，是广州市民喜欢游玩之地．小明、小丽两家人决定周末去游玩，并用抽卡片的方式从白云山、越秀山、莲花山和大夫山（分别记为、、、）选出一个景点．他们准备了张不透明的卡片，正面分别写上、、和．卡片除正面字母不同外其余均相同．
（1）小明随机抽取一张卡片，则抽取到卡片的概率是_______；
（2）小明随机抽取一张卡片后，放回洗匀，小丽再随机抽取一张卡片，请用列或画树状图的方法求他们都抽取到同一地点的概率．
21．（本小题满分8分）
如图，二次函数的图象与轴交于点和点，点轴交于点．
（1）求二次函数的解析式；
（2）求点坐标，并结合图象写出时，的取值范围；
22．（本小题满分10分）
为积极响应国家“旧房改造”工程，某市推出《加快推进旧房改造工作的实施方案》推进新型城镇化建设，改善民生，优化城市建设．
（1）根据方案，该市的旧房改造户数从年底的万户增长到年底的万户，求该市这两年旧房改造户数的平均年增长率；
（2）该市计划对某小区进行旧房改造，如果计划改造户，计划投入改造费用平均
元户，且计划改造的户数每增加户，投入改造费平均减小元户，求旧房改造申报的最高投入费用是多少元？
23．（本小题满分10分）
如图，在等腰中，．
（1）尺规作图：以为直径作，标出点（保留作图痕迹，不写作法）；
（2）在（1）中所作的交边于点，过点作交于点，延长
交的延长线于点，
①求证：是的切线；
②若，，求的长．
24．（本小题满分10分）
如图，在四边形中，，，，延长线段，将射线绕点逆时针旋转至射线，点关于的对称点为，直线与射线相交于，连接，，
（1）当时，如图1，为的中点，连接，求的度数；
（2）如图2，随着的变化，射线在内部运动，
①当落在直线上时，求的运动路径长（用含的代数式表示）；
②若，，在射线的运动过程中，求的面积最大值．
25．（本小题满分12分）
在平面直角坐标系中，抛物线（，，为常数，且）经过和两点．
（1）求和的值（用含的代数式表示）；
（2）若该抛物线开口向下，且经过，两点，当时，
随的增大而减小，求的取值范围；
（3）已知点，，若该抛物线与线段恰有一个公共点时，结合函数图
象，求的取值范围．