新教材2024版高中数学第五章三角函数5.1任意角和蝗制5.1.2蝗制课件新人教A版必修第一册

这是一份新教材2024版高中数学第五章三角函数5.1任意角和蝗制5.1.2蝗制课件新人教A版必修第一册，共39页。

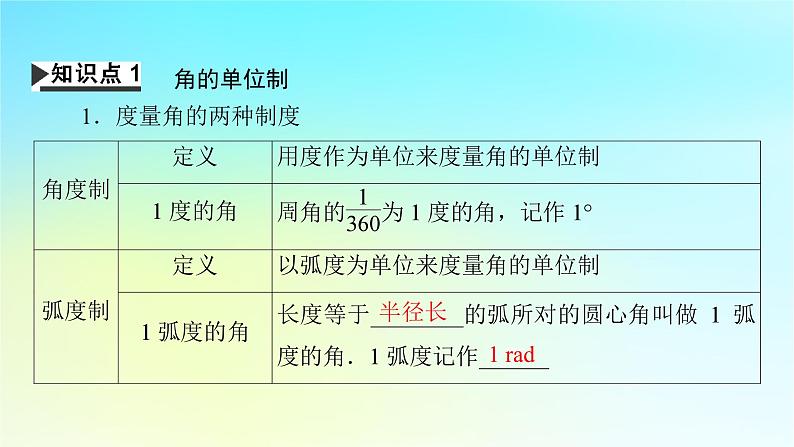
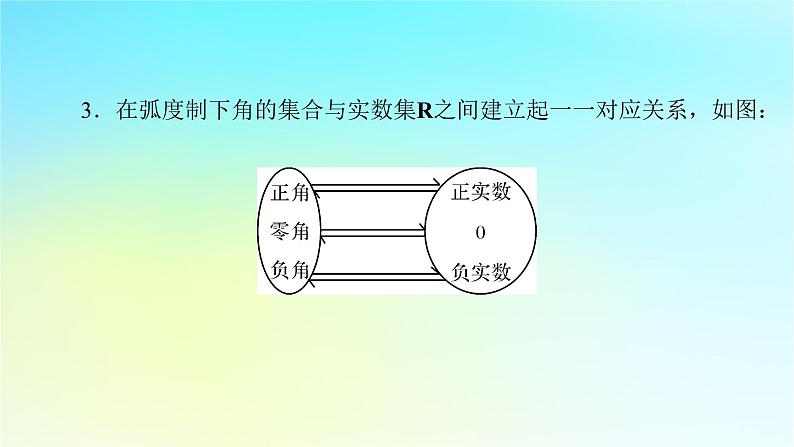
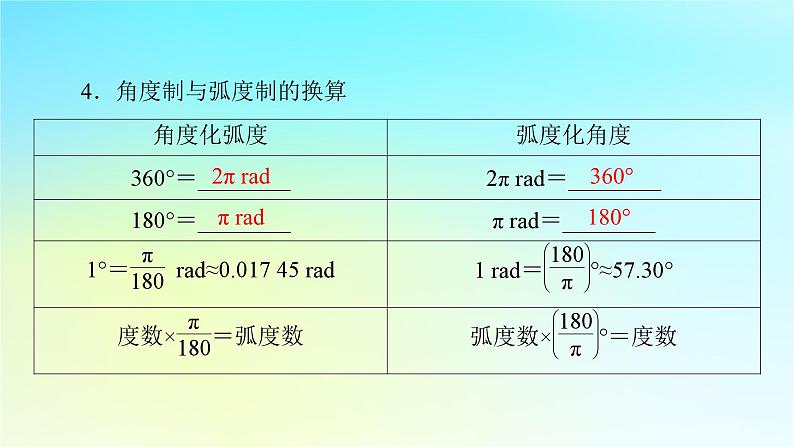
第五章　三角函数5.1　任意角和弧度制5.1.2　弧度制| 自 学 导 引 | 　　　　角的单位制1．度量角的两种制度半径长　1 rad 　2．弧度数的计算(1)正角：正角的弧度数是一个________．(2)负角：负角的弧度数是一个________．(3)零角：零角的弧度数是______．正数　负数　0 　3．在弧度制下角的集合与实数集R之间建立起一一对应关系，如图：4．角度制与弧度制的换算2π rad　360°　π rad　180° 　【答案】(1)×　(2)√　(3)√【解析】(1)1弧度是长度等于半径的弧所对的圆心角．(2)“1弧度的角”的大小等于半径长的圆弧所对的圆心角，是一个定值，与所在圆的半径大小无关．　　　　扇形的弧长及面积公式设扇形的半径为R，弧长为l，α为其圆心角，则l＝αR　【预习自测】圆的半径是6 cm，则圆心角为15°的扇形面积是________．| 课 堂 互 动 | 弧度制下与角α终边相同的角的表示在弧度制下，与角α的终边相同的角可以表示为{β|β＝2kπ＋α，k∈Z}，即与角α终边相同的角可以表示成α加上2π的整数倍．提醒：(1)注意角度与弧度不能混用；(2)各终边相同的角需加2kπ，k∈Z．2．已知角α＝2 010°．(1)将α改写成β＋2kπ(k∈Z,0≤β＜2π)的形式，并指出α是第几象限的角；(2)在区间[－5π，0)上找出与α终边相同的角．题型3　扇形的弧长公式及面积公式的应用　　　　一个扇形所在的圆半径为5，该扇形弧长为5．(1)求该扇形的面积；(2)求该扇形的中心角弧度数．提醒：当扇形周长一定时，求扇形面积的最大值，需把面积S转化为关于r的二次函数，但要注意r的取值范围，特别注意一个扇形的弧长必须满足0＜l＜2πr．3．已知扇形AOB的周长为10 cm．(1)若这个扇形的面积为4 cm2，求扇形圆心角的弧度数；(2)求该扇形的面积取得最大值时，圆心角的大小及弧长．解：设扇形圆心角的弧度数为θ(0＜θ＜2π)，弧长为l，半径为r，面积为S．易错警示　角度和弧度混用致错　　　　求终边在如图所示的阴影部分(不包括边界)内的角的集合．错解一：{α|k·360°＋330°＜α＜k·360°＋60°，k∈Z}．错解二：{α|2kπ－30°＜α＜2kπ＋60°，k∈Z}．易错防范：错解一中，若给k赋一个值，集合中不等式右边的角反而小于左边的角．错解二中，同一不等式中混用了角度制与弧度制．同一个问题(或题目)中使用的度量单位要统一，要么用角度制单位，要么用弧度制单位，不能将两者混用．| 素 养 达 成 | 1．角的概念推广后，在弧度制下，角的集合与实数集R之间建立起一一对应的关系：每一个角都有唯一的一个实数(即这个角的弧度数)与它对应；反过来，每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应(体现了数学运算核心素养)．2．解答角度与弧度的互化问题的关键在于充分利用“180°＝π rad”这一关系式．3．在弧度制下，扇形的弧长公式及面积公式都得到了简化，具体应用时，要注意角的单位取弧度．1．(题型1)(多选)下列说法中，正确的是 (　　)A．半圆所对的圆心角是π radB．周角的大小等于2πC．1弧度的圆心角所对的弧长等于该圆的半径D．长度等于半径的弦所对的圆心角的大小是1弧度【答案】ABC【答案】B【答案】B