





还剩24页未读,
继续阅读
成套系列资料,整套一键下载
- 新教材2024版高中数学第五章三角函数5.2三角函数的概念5.2.1三角函数的概念课件新人教A版必修第一册 课件 0 次下载
- 新教材2024版高中数学第五章三角函数5.3诱导公式第二课时课件新人教A版必修第一册 课件 0 次下载
- 新教材2024版高中数学第五章三角函数5.4三角函数的图象与性质5.4.2正弦函数余弦函数的性质第一课时正弦函数余弦函数的周期性与奇偶性课件新人教A版必修第一册 课件 0 次下载
- 新教材2024版高中数学第五章三角函数5.4三角函数的图象与性质5.4.2正弦函数余弦函数的性质第二课时正弦函数余弦函数的单调性与最值课件新人教A版必修第一册 课件 0 次下载
- 新教材2024版高中数学第五章三角函数5.4三角函数的图象与性质5.4.3正切函数的性质与图象课件新人教A版必修第一册 课件 0 次下载
数学必修 第一册5.4 三角函数的图象与性质教课内容ppt课件
展开
这是一份数学必修 第一册5.4 三角函数的图象与性质教课内容ppt课件,共32页。PPT课件主要包含了答案A,答案3等内容,欢迎下载使用。
| 自 学 导 引 |
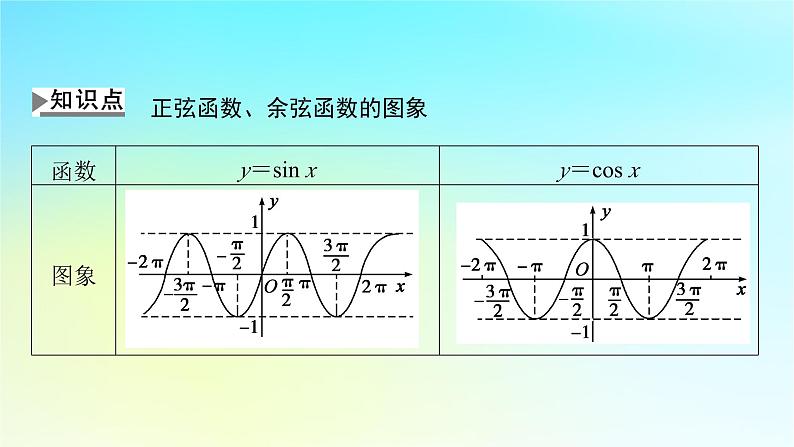
正弦函数、余弦函数的图象
正弦函数y=sin x,x∈R的图象叫做正弦曲线,余弦函数y=cs x,x∈R的图象叫做余弦曲线.
【预习自测】判断下列说法是否正确.(正确的画“√”,错误的画“×”)(1)正弦函数y=sin x的图象向左右和上下无限伸展.( )(2)函数y=sin x与y=sin (-x)的图象完全相同.( )(3)函数y=cs x的图象关于(0,0)对称.( )【答案】(1)× (2)× (3)×【解析】(1)正弦函数y=sin x的图象向左右无限伸展,但上下限定在直线y=1和y=-1之间.(2)二者图象不同,而是关于x轴对称.(3)函数y=cs x的图象关于y轴对称.
| 课 堂 互 动 |
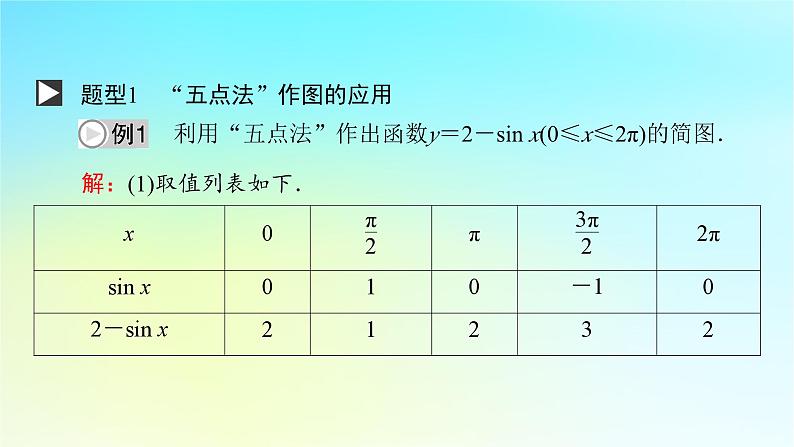
题型1 “五点法”作图的应用 利用“五点法”作出函数y=2-sin x(0≤x≤2π)的简图.
解:(1)取值列表如下.
(2)描点连线,如图所示.
用“五点法”画函数y=A sin x+b(A≠0)或y=A cs x+b(A≠0)在[0,2π]上简图的步骤(1)列表:
1.利用“五点法”作出函数y=-1-cs x(0≤x≤2π)的简图.解:(1)取值列表如下.
利用三角函数图象解sin x>a(或cs x>a)的三个步骤(1)作出直线y=a,y=sin x(或y=cs x)的图象.(2)确定sin x=a(或cs x=a)的x值.(3)确定sin x>a(或cs x>a)的解集.提醒:解三角不等式sin x>a,如果不限定范围时,一般先利用图象求出x∈[0,2π]范围内x的取值范围,然后根据终边相同角的同一三角函数值相等,写出原不等式的解集.
题型3 正弦、余弦曲线与其他曲线的交点问题 求方程sin x+2|sin x|-|lg2x|=0解的个数.
判断方程解的个数的关注点(1)确定方程解的个数问题,常借助函数图象用数形结合的方法求解.(2)当在同一坐标系中作两个函数的图象时,要注意其相对位置,常借助于函数值的大小来确定.
3.方程x2-cs x=0的实数解的个数是________.【答案】2 【解析】作函数y=cs x与y=x2的图象,如图所示,由图象可知原方程有两个实数解.
易错警示 利用正弦函数、余弦函数图象判断方程根的个数没有找准临界点致误 方程sin x=lg x的实数根有( )A.1个B.2个C.3个D.无穷多个
错解:如图所示,y=sin x与y=lg x的图象,有且只有1个公共点.故选A.
易错防范:作y=lg x图象时,没有找准临界点的坐标,只作出了草图.
正解:在同一平面直角坐标系中作函数y=sin x与y=lg x的图象.由图中可以看出两函数图象有三个交点,故原方程的实根有3个.故选C.
| 素 养 达 成 |
1.对“五点法”画正弦函数图象的理解(体现了直观想象核心素养).(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.(2)正弦型函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.
2.作函数y=a sin x+b的图象的步骤
【答案】D 【解析】函数y=-sin x与y=sin x的图象关于x轴对称.
2.(题型1,2)(多选)下列关于正弦函数、余弦函数的图象的描述,正确的是( )A.都可由[0,2π]内的图象向上、向下无限延展得到B.都是对称图形C.都与x轴有无数个交点D.y=-cs x的图象与y=cs x的图象关于x轴对称【答案】BCD
| 自 学 导 引 |
正弦函数、余弦函数的图象
正弦函数y=sin x,x∈R的图象叫做正弦曲线,余弦函数y=cs x,x∈R的图象叫做余弦曲线.
【预习自测】判断下列说法是否正确.(正确的画“√”,错误的画“×”)(1)正弦函数y=sin x的图象向左右和上下无限伸展.( )(2)函数y=sin x与y=sin (-x)的图象完全相同.( )(3)函数y=cs x的图象关于(0,0)对称.( )【答案】(1)× (2)× (3)×【解析】(1)正弦函数y=sin x的图象向左右无限伸展,但上下限定在直线y=1和y=-1之间.(2)二者图象不同,而是关于x轴对称.(3)函数y=cs x的图象关于y轴对称.
| 课 堂 互 动 |
题型1 “五点法”作图的应用 利用“五点法”作出函数y=2-sin x(0≤x≤2π)的简图.
解:(1)取值列表如下.
(2)描点连线,如图所示.
用“五点法”画函数y=A sin x+b(A≠0)或y=A cs x+b(A≠0)在[0,2π]上简图的步骤(1)列表:
1.利用“五点法”作出函数y=-1-cs x(0≤x≤2π)的简图.解:(1)取值列表如下.
利用三角函数图象解sin x>a(或cs x>a)的三个步骤(1)作出直线y=a,y=sin x(或y=cs x)的图象.(2)确定sin x=a(或cs x=a)的x值.(3)确定sin x>a(或cs x>a)的解集.提醒:解三角不等式sin x>a,如果不限定范围时,一般先利用图象求出x∈[0,2π]范围内x的取值范围,然后根据终边相同角的同一三角函数值相等,写出原不等式的解集.
题型3 正弦、余弦曲线与其他曲线的交点问题 求方程sin x+2|sin x|-|lg2x|=0解的个数.
判断方程解的个数的关注点(1)确定方程解的个数问题,常借助函数图象用数形结合的方法求解.(2)当在同一坐标系中作两个函数的图象时,要注意其相对位置,常借助于函数值的大小来确定.
3.方程x2-cs x=0的实数解的个数是________.【答案】2 【解析】作函数y=cs x与y=x2的图象,如图所示,由图象可知原方程有两个实数解.
易错警示 利用正弦函数、余弦函数图象判断方程根的个数没有找准临界点致误 方程sin x=lg x的实数根有( )A.1个B.2个C.3个D.无穷多个
错解:如图所示,y=sin x与y=lg x的图象,有且只有1个公共点.故选A.
易错防范:作y=lg x图象时,没有找准临界点的坐标,只作出了草图.
正解:在同一平面直角坐标系中作函数y=sin x与y=lg x的图象.由图中可以看出两函数图象有三个交点,故原方程的实根有3个.故选C.
| 素 养 达 成 |
1.对“五点法”画正弦函数图象的理解(体现了直观想象核心素养).(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.(2)正弦型函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.
2.作函数y=a sin x+b的图象的步骤
【答案】D 【解析】函数y=-sin x与y=sin x的图象关于x轴对称.
2.(题型1,2)(多选)下列关于正弦函数、余弦函数的图象的描述,正确的是( )A.都可由[0,2π]内的图象向上、向下无限延展得到B.都是对称图形C.都与x轴有无数个交点D.y=-cs x的图象与y=cs x的图象关于x轴对称【答案】BCD













