2022-2023学年山西省运城市芮城县九年级（上）期末数学试卷（含解析）

这是一份2022-2023学年山西省运城市芮城县九年级（上）期末数学试卷（含解析），共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.反比例函数y=6x的图象分别位于( )
A. 第一、第三象限B. 第一、第四象限C. 第二、第三象限D. 第二、第四象限
2.抛物线y=(x−1)2+2与y轴交点坐标为( )
A. (0,1)B. (0,2)C. (1,2)D. (0,3)
3.如图，在5×6的正方形网格中，点A，B，C都在格点上，则tan∠ABC的值为( )
A. 22
B. 2
C. 1
D. 33
4.在一个不透明的袋中有2个红球和1个白球，这些球除颜色外部相同.搅匀后，随机从中摸出一个球.记下颜色后放回袋子中，充分搖匀后，再从中随机摸出一个球，两次都摸到红球的概率是( )
A. 13B. 19C. 59D. 49
5.关于矩形的性质、下面说法错误的是( )
A. 矩形的四个角都是直角B. 矩形的两组对边分别相等
C. 矩形的两组对边分别平行D. 矩形的对角线互相垂直平分且相等
6.抛物线y=a(x−2)2+k的开口向上，点A(−1,y1)，B(3,y2)是抛物线上两点，则y1，y2的大小关系是( )
A. y1>y2B. y17.二次函数y=ax2+bx+c的图象如图所示，则一次函数y=abx+c的图象大致是( )
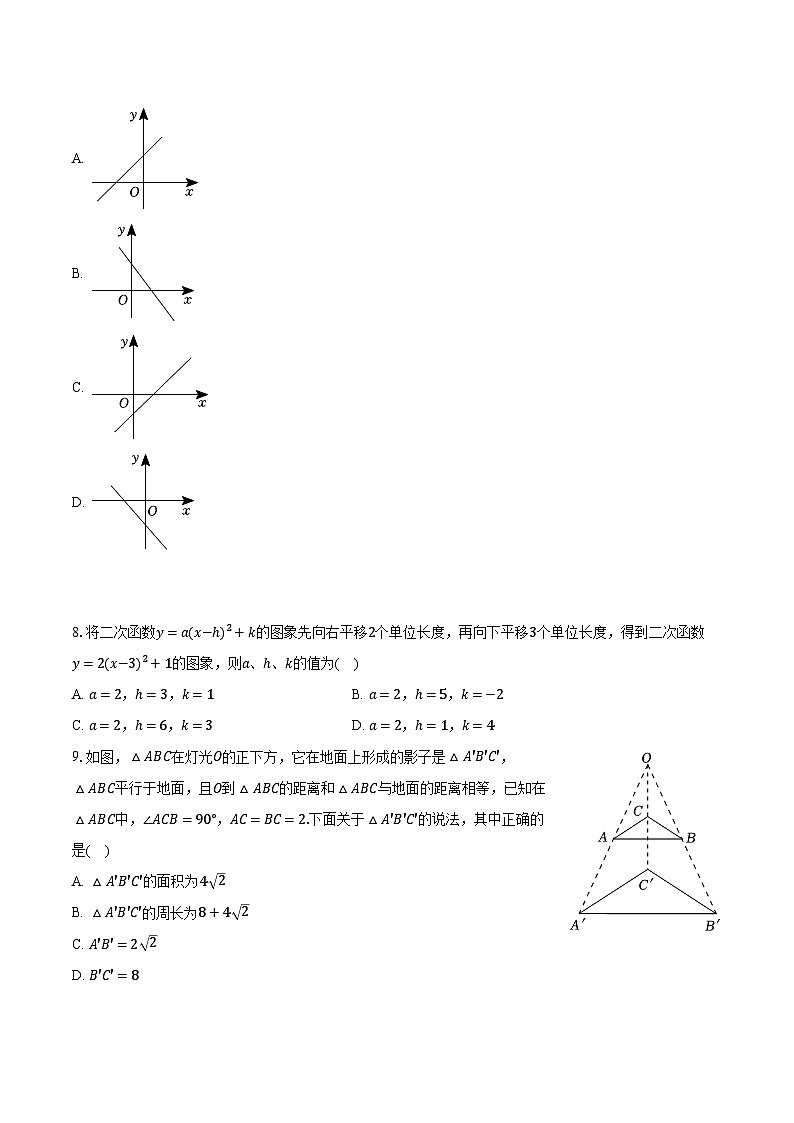
A.
B.
C.
D.
8.将二次函数y=a(x−h)2+k的图象先向右平移2个单位长度，再向下平移3个单位长度，得到二次函数y=2(x−3)2+1的图象，则a、h、k的值为( )
A. a=2，h=3，k=1B. a=2，h=5，k=−2
C. a=2，h=6，k=3D. a=2，h=1，k=4
9.如图，△ABC在灯光O的正下方，它在地面上形成的影子是△A′B′C′，△ABC平行于地面，且O到△ABC的距离和△ABC与地面的距离相等，已知在△ABC中，∠ACB=90°，AC=BC=2.下面关于△A′B′C′的说法，其中正确的是( )
A. △A′B′C′的面积为4 2
B. △A′B′C′的周长为8+4 2
C. A′B′=2 2
D. B′C′=8
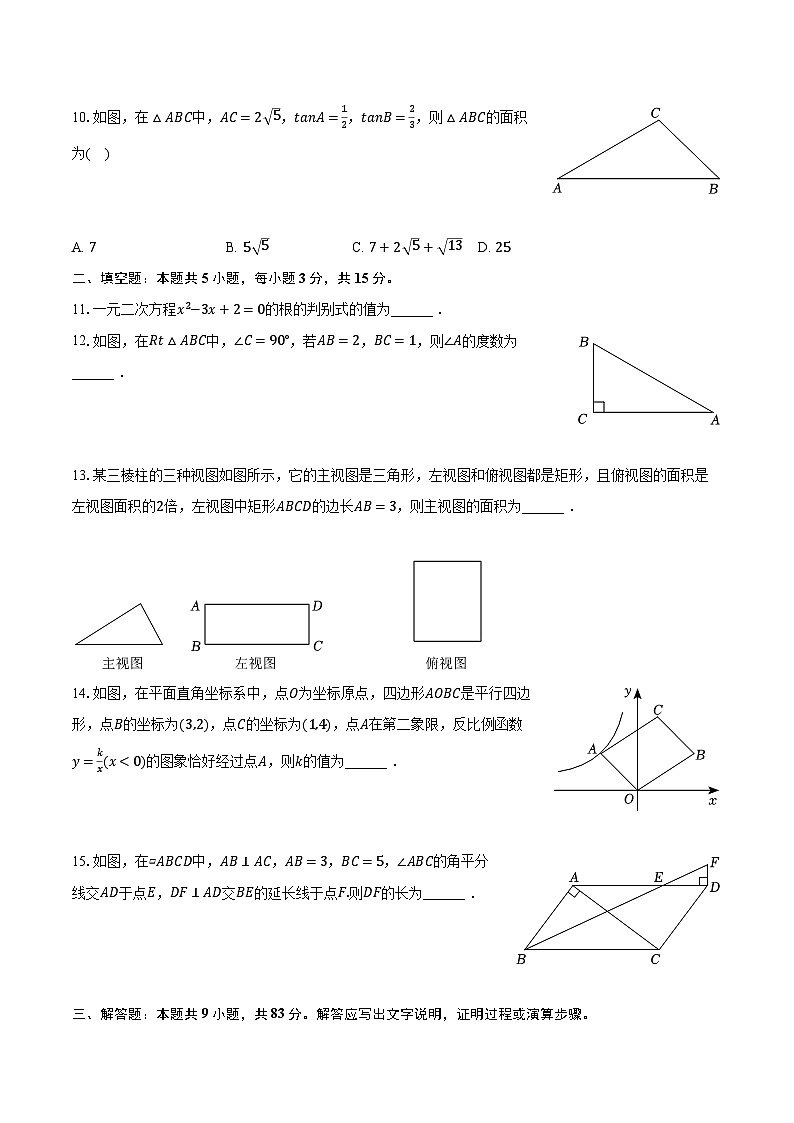
10.如图，在△ABC中，AC=2 5，tanA=12，tanB=23，则△ABC的面积为( )
A. 7B. 5 5C. 7+2 5+ 13D. 25
二、填空题：本题共5小题，每小题3分，共15分。
11.一元二次方程x2−3x+2=0的根的判别式的值为______ ．
12.如图，在Rt△ABC中，∠C=90°，若AB=2，BC=1，则∠A的度数为______ ．
13.某三棱柱的三种视图如图所示，它的主视图是三角形，左视图和俯视图都是矩形，且俯视图的面积是左视图面积的2倍，左视图中矩形ABCD的边长AB=3，则主视图的面积为______ ．
14.如图，在平面直角坐标系中，点O为坐标原点，四边形AOBC是平行四边形，点B的坐标为(3,2)，点C的坐标为(1,4)，点A在第二象限，反比例函数y=kx(x<0)的图象恰好经过点A，则k的值为______ ．
15.如图，在▱ABCD中，AB⊥AC，AB=3，BC=5，∠ABC的角平分线交AD于点E，DF⊥AD交BE的延长线于点F.则DF的长为______ ．
三、解答题：本题共9小题，共83分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
计算：tan60°−2cs30°+ 2sin45°．
17.(本小题8分)
将抛物线y=2x2−4x+1化成y=a(x−h)2+k的形式，并直接写出它的对称轴．
18.(本小题7分)
如图，为了测量某树AB的高度，小明在点C处测得树顶A的仰角为30°，他朝树前行10米到达点D处，又测得树顶A的仰角为60°，已知点A，B，C，D在同一平面内，求树AB的高度.(结果保留根号)
19.(本小题8分)
某种服装平均每天销售20件，每件赢利30元，在每件降价幅度不超过10元的情况下，若每件降价1元，则每天可多售5件，如果每天要赢利1200元，每件应降价多少元？
20.(本小题10分)
如图，一次函数y1=kx+b与反比例函数y2=mx的图象交于A(a,4)，B(−3,−2)两点，直线AB与x轴，y轴分别交于D，C两点．
(1)求一次函数与反比例函数的表达式；
(2)求证：AD=BC；
(3)点P是x轴正半轴上的一点，连接PA，PC，若S△PAC=4，请直接写出点P的坐标．
21.(本小题9分)
如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点D从点B出发，沿BC以每秒1个单位的速度向点C运动；动点E同时从点C出发，沿CA以每秒1个单位的速度向点A运动，连接DE，设运动时间为t秒．
(1)在运动的过程中，当sin∠EDC=35时，则运动时间t的值为______ ；
(2)当△CDE∽△CAB时，求t的值；
(3)设四边形ADBE的面积为y，求y与t的函数关系式，并求出当t为何值时，y有最小值，最小值是多少？
22.(本小题9分)
阅读理解题：一次数学综合实践活动课上，小亮发现并证明了关于三角形角平分线的一个结论.如图1，已知AD是△ABC的角平分线，可得：ABAC=BDCD，小亮的证明过程(部分)如下：
证明：过点C作CE/​/AB，交AD的延长线于点E，
∵CE/​/AB，
∴∠E=∠BAE，∠B=∠BCE．
∴△ABD∽△ECD．
∴ABCE=BDCD．
……

(1)请按照上面小亮的证明思路.写出该证明的剩余部分；
(2)如图2，在△ABC中，AD是△ABC的角平分线，已知BDBC=35，则ABAC的值为______ ．
(3)如图3，在矩形ABCD中，点E是CD上一点，已知AB=3，AD=4，DE=1，连接BE，AF平分∠BAD与BE交于点F，则BF的长为______ ．
23.(本小题12分)
综合与实践．
问题情境：课堂上老师展示了一张直角三角形纸片.请同学们进行折纸活动，已知在Rt△ABC中.∠ACB=90°，点D、F分别是BC、AB上的一点.连接DF．

(1)如图1.小红将△BDF沿直线DF折叠，点B恰好落在BC上点E处，若S△BDFS四边形ACEF=17，则DEDC的值______ ；
(2)如图2，小明将△BDF沿直线DF折叠，点B落在AC上点E处，若FE⊥AC，求证：四边形BDEF是菱形；
(3)如图3.小亮将△BDF沿直线DF折叠，点B落在AC延长线上点E处，且EF平分∠AED，若AC=3，BC=4，求CE的长．
24.(本小题12分)
综合与探究：如图，二次函数y=−12x2+x+4的图象与x轴交于A，B两点(点A在点B的左则)，与y轴交于点C，点D是抛物线的顾点.抛物线的对称轴交x轴于点E，点P是第一象限内且在对称轴右侧二次函数图象上的一个动点，设点P的横坐标为m，点F的坐标为(0,−3)，连接FP，FP分别与x轴，对称轴交于点G，H．
(1)求A，B，C三点的坐标并直接写出顶点D的坐标；
(2)当FG：GP=6：5时.求点P的坐标；
(3)试探究：在点P运动过程中，是否存在点P，使得∠FHE=135°，若存在，请直接写出m的值；若不存在，请说明理由．
答案和解析
1.【答案】A
【解析】【分析】
根据反比例函数的性质结合k=6>0，即可判断出正确答案．
本题考查反比例函数的图象和性质，解答本题的关键是明确当k>0时，反比例函数图象的两个分支位于第一、三象限．
【解答】
解：反比例函数y=6x中，k=6>0，
∴该反比例函数图象的两个分支位于第一、三象限．
故选：A．
2.【答案】D
【解析】解：将x=0代入y=(x−1)2+2，得y=3，
所以抛物线与y轴的交点坐标是(0,3)．
故选D．
将x=0代入y=(x−1)2+2，计算即可求得抛物线与y轴的交点坐标．
本题考查了二次函数图象上点的坐标特征，根据y轴上点的横坐标为0求出交点的纵坐标是解题的关键．
3.【答案】C
【解析】解：连接AC，
∵AC= 12+32= 10，AB= 12+32= 10，BC= 22+42= 20=2 5，
∴AC2+AB2=BC2，
∴△ABC是直角三角形，
在Rt△ABC中，tan∠ABC=ACAB= 10 10=1，
故选：C．
连接AC，得出△ABC是直角三角形，再求正切即可．
本题考查正切函数，直角三角形的判定，得出△ABC是直角三角形是解题的关键．
4.【答案】D
【解析】解：画树状图如下：
由树状图可知，共有9种等可能结果，其中两次都摸到红球的有4种结果，
∴两次都摸到红球的概率为49，
故选：D．
首先根据题意画出树状图，由树状图求得所有等可能的结果与两次都摸到红球的情况，然后利用概率公式求解即可求得答案．注意此题属于放回实验．
本题考查的是用列表法或树状图法求概率的知识．注意画树状图与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．
5.【答案】D
【解析】解：A、矩形的四个角都是直角，说法正确，不符合题意；
B、矩形的两组对边分别相等，说法正确，不符合题意；
C、矩形的两组对边分别平行，说法正确，不符合题意；
D、矩形的对角线互相平分且相等但不一定垂直，说法错误，符合题意；
故选：D．
根据矩形的性质对选项逐一进行判断即可．
本题考查了矩形的性质，矩形的性质：①平行四边形的性质矩形都具有；
②角：矩形的四个角都是直角；
③边：邻边垂直；
④对角线：矩形的对角线相等；
⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．
6.【答案】A
【解析】解：∵抛物线y=a(x−2)2+k的图象与性质，确定抛物线开口向上，对称轴为x=2，
∴函数y=a(x−2)2+k可取到最小值，
∴抛物线上的点离对称轴越近，对应的函数值越小，
∵点A(−1,y1)，B(3,y2)是抛物线上两点，A(−1,y1)到对称轴距离为2−(−1)=3，B(3,y2)到对称轴距离为3−2=1，1<3，
∴B(3,y2)到对称轴距离比A(−1,y1)到对称轴距离近，
∴y1>y2，
故选：A．
根据抛物线y=a(x−2)2+k的图象与性质，确定抛物线开口向上，对称轴为x=2，函数y=a(x−2)2+k可取到最小值，从而抛物线上的点离对称轴越近，则对应的函数值越小，根据点A(−1,y1)，B(3,y2)是抛物线上两点，A(−1,y1)到对称轴距离为2−(−1)=3，B(3,y2)到对称轴距离为3−2=1，由于1<3得到B(3,y2)到对称轴距离比A(−1,y1)到对称轴距离近，则y1>y2．
本题考查二次函数图象与性质比较函数值大小，掌握利用点到对称轴距离比较大小的方法是解决问题的关键．
7.【答案】C
【解析】解：由二次函数的图象可得，
∵开口向上，图象与y轴的负半轴相交，
∴a>0，c<0，
∵对称轴在y轴的左侧，a>0，
∴b>0，
∵a>0，b>0，
∴ab>0，
∴一次函数的图象经过第一、三、四象限，
故选：C．
根据二次函数的图象可以判断a、b、c的符号，从而可以确定一次函数的图象经过的象限，本题得以解决．
本题考查二次函数的图象、一次函数的图象，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．
8.【答案】D
【解析】解：∵将二次函数y=a(x−h)2+k的图象先向右平移2个单位长度，再向下平移3个单位长度，得到二次函数y=a(x−h−2)2+k−3，与y=2(x−3)2+1为同一个解析式，
∴a=2−h−=−3k−3=1，
解得a=2h=1k=4，
故选：D．
根据函数图象的平移法则：左加右减、上加下减按要求平移后将两个函数解析式对比即可得到答案．
本题考查二次函数图象平移，熟练掌握函数图象的平移法则：左加右减、上加下减得到相应函数解析式是解决问题的关键．
9.【答案】B
【解析】解：由题意可知，AB= AC2+BC2= 22+22=2 2，
∴C△ACB=AC+BC+AB=4+2 2，S△ACB=12AC⋅BC=12×2=2，
∴△A′B′C′～△ABC且相似比为2：1，
∵S△A′B′C′S△ABC=(21)2，
∴S△A′B′C′=4S△ABC=4×2=8，故A选项错误，不符合题意；
∵C△A′B′C′C△ABC=21，
∴C△A′B′C′=2C△ABC=8+4 2，故B选项正确，符合题意；
∵A′B′AB=B′C′BC=21，
∴A′B′=2AB=4 2，B′C′=2BC=4，故C、D选项错误，不符合题意；
故选：B．
分别求出AB=2 2、C△ACB=4+2 2、S△ACB=2再依据相似三角形的性质进行判断即可．
本题考查了相似三角形性质的应用；解题的关键是掌握相似三角形的边长和周长比等于相似比，面积比等于相似比的平方．
10.【答案】A
【解析】解：过点C作CD⊥AB于点D，如图所示：
∴∠ADC=∠BDC=90°，
在Rt△ACD中，
∵tanA=12，
∴CDAD=12，
∴设CD=x，则AD=2x，
∵AD2+CD2=AC2，
∴(2x)2+x2=(2 5)2，
解得：x=2或x=−2(舍去)，
∴AD=4，CD=2，
在Rt△BCD中，
∵tanB=CDBD=23，
∴BD=3，
∴AB=AD+BD=7，
∴S△ABC=12AB×CD=12×7×2=7，故A正确．
故选：A．
过点C作CD⊥AB于点D，根据正切函数的定义和勾股定理求出AD=4，CD=2，根据正切函数值求出BD=3，得出△ABC的面积即可．
本题主要考查了三角函数的应用，三角形面积的计算，勾股定理，解题的关键是熟练掌握三角函数的定义，求出AB=7．
11.【答案】1
【解析】解：∵a=1，b=−3，c=2，
∴△=b2−4ac=(−3)2−4×1×2=1，
故答案为：1．
根据根的判别式等于b2−4ac，代入求值即可．
本题考查了根的判别式，熟记一元二次方程ax2+bx+c=0(a≠0)的根的判别式的公式为△=b2−4ac．
12.【答案】30°
【解析】解：∵在Rt△ABC中，∠C=90°，AB=2，BC=1．
∴sinA=BCAB=12，
∴∠A=30°，
故答案为：30°．
根据特殊角的三角函数，在Rt△ABC中，∠C=90°，AB=2，BC=1，从而得到sinA=BCAB=12，从而确定∠A=30°．
本题考查特殊角的三角函数值，掌握特殊角的三角函数值定义是解决问题的关键．
13.【答案】9
【解析】解：∵主视图、俯视图与左视图的长相等，若左视图中矩形ABCD的边长AB=3，俯视图的面积是左视图面积的2倍，
∴主视图的宽为2AB=6，
∵主视图与左视图关系知主视图三角形的高为AB=3，
∴主视图的面积为12×6×3=9，
故答案为：9．
根据三视图关系可知，主视图、俯视图与左视图的长相等，由左视图中矩形ABCD的边长AB=3，俯视图的面积是左视图面积的2倍，可知主视图的宽为2AB=6，由主视图与左视图关系可知，主视图三角形的高为AB=3，从而利用三角形面积公式即可得到主视图的面积为12×6×3=9．
本题考查三视图边长关系，熟练掌握“长对正、高平齐、宽相等”，通过三视图准确得到相应图形的边长是解决问题的关键．
14.【答案】−4
【解析】解：∵四边形AOBC是平行四边形，
∴xB−xO=xC−xA，yB−yO=yC−yA，
∵B(3,2)，C(1,4)，O(0,0)，
∴3−0=1−xA，2−0=4−yA，
解得xA=−2，yA=2，
∴A(−2,2)，
将A(−2,2)代入y=kx并解得k=−4，
故答案为：−4．
根据平行四边形的性质和点B，C，O的坐标求出点A的坐标，再把点A的坐标代入y=kx即可求解．
本题考查了反比例函数图象上点的坐标特点，熟练掌握平行四边形的性质是解题的关键．
15.【答案】1
【解析】解：令AC与BE交于O点，如图所示：
∵AB⊥AC，AB=3，BC=5，
∴AC= BC2−AB2= 52−32=4，
在平行四边形ABCD中，AD//BC，AD=BC=5，DC=AB=3，
∴∠AEB=∠EBC，
∵∠ABC的角平分线交AD于点E，
∴∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AE=AB=3，
∴DE=AD−AE=5−3=2，
∵∠AOE=∠COB，
∴△AOE∽△COB，
∴AOOC=AEBC=35，
∵AC=4，
∴AO=32，
∵∠FED=∠AEB，
∴∠FED=∠ABO，
∵DF⊥AD交BE的延长线于点F，
∴∠FDE=∠BAC=90°，
∴△BOA∽△EFD，
∴AODF=ABED，
即DF=AO⋅EDAB=32×23=1，
故答案为：1．
令AC与BE交于O点，如图所示，根据AB⊥AC，AB=3，BC=5，利用勾股定理得到AC=4，再由平行四边形ABCD中，∠ABC的角平分线交AD于点E，DF⊥AD交BE的延长线于点F，得到AE=AB=3，DE=AD−AE=5−3=2，由△AOE∽△COB得到AO=32，再由△BOA∽△EFD，从而AODF=ABED，代值求解即可得到答案．
本题考查利用相似求线段长，涉及勾股定理、平行四边形性质、等腰三角形的判定与性质、相似三角形的判定与性质等知识，本题综合性较强，熟练掌握相关几何知识的性质是解决问题的关键．
16.【答案】解：原式= 3−2× 32+ 2× 22
= 3− 3+1
=1．
【解析】直接利用特殊角的三角函数值分别代入，再利用二次根式的混合运算法则化简，进而计算得出答案．
此题主要考查了特殊角的三角函数值以及二次根式的混合运算，正确化简各数是解题关键．
17.【答案】解：y=2x2−4x+1
=2(x2−2x)+1
=2(x2−2x+1−1)+1
=2(x−1)2−1，
∴抛物线的对称轴为直线x=1．
【解析】运用配方法将抛物线解析式整理为二次函数的顶点式即可得出答案．
本题考查了二次函数的性质，熟练掌握配方法是解本题的关键．
18.【答案】解：方法一：设AB=x米，
在Rt△ABD中，∠ABD=90°，
∵tan∠ADB=ABBD，
∴BD=ABtan60∘=x 3= 3x3，
在Rt△ABC中，∠ABC=90°，
∵tan∠ACB=ABBC，
∴BC=ABtan30∘=x 33= 3x，
∵CD=BC−BD，
∴10= 3x− 33x，
∴x=5 3，
答：树AB的高度为5 3米．
方法二：∵∠ADB=∠C+∠CAD，∠C=30°，∠ADB=60°，
∴∠CAD=∠C=30°，
∴AD=CD=10，
在Rt△ABD中，∠ABD=90°，
∵sin∠ADB=ABAD，
∴AB=AD⋅sin60°=10× 32=5 3，
答：树AB的高度为5 3米．
【解析】根据解直角三角形的方法，即可求解．
本题考查了解直角三角形的应用，根据题意和图形，采用适当的方法解直角三角形是解决本题的关键．
19.【答案】解：设每件降价x元，
根据题意可得：(30−x)(20+5x)=1200，
化简得：x2−26x+120=0，
解得x1=20，x2=6，
∵20>10，
∴x=20舍去，
答：每件应降价6元．
【解析】根据题意，设每件降价x元，由等量关系列出方程(30−x)(20+5x)=1200，解一元二次方程，由每件降价幅度不超过10元的情况下，进行取舍即可得到答案．
本题考查一元二次方程解实际应用题，读懂题意，找到等量关系列出方程是解决问题的关键．
20.【答案】(1)解：∵点B(−3,−2)在反比例函数y=mx的图象上，
∴m=−3×(−2)=6．
∴反比例函数的表达式为y=6x．
∵点A(a,4)在反比例函数y=6x的图象上，
∴a=64=32．
∴点A的坐标为点(32,4)．
将点A(32,4),B(−3,−2)代入y=kx+b中，得−2=−3k+b4=32k+b，
解得：k=43b=2，
∴一次函数的表达式为y=43x+2；
(2)证明：方法一：作AM⊥x轴于点M，BN⊥y轴于点N，

则AM=4,OM=32,BN=3,ON=2.∠AMD=∠BNC=90°，
当x=0时，y=2；当y=0时，x=32．
∴点C的坐标为(0,2)；点D的坐标为(−32,0)，
∴OC=2,OD=32．
∴CN=OC+ON=4，DN=OD+OM=3．
∴AM=CN=4，BN=DM=3．
在△ADM与△CBN中，
AM=CN∠AMD=∠CNBDM=BN，
∴△ADM≌△CBN(SAS)．
∴AD=BC．
方法二：作AM⊥y轴于点M，BN⊥x轴于点N，

则AM=32,OM=4,BN=2,ON=3.∠AMC=∠BND=90°，
当x=0时，y=2；当y=0时，x=32．
∴点C的坐标为(0,2)；点D的坐标为(−32,0)．
∴OC=2,OD=32．
∴CM=OM−OC=4−2=2．
∴DN=ON−OD=3−32=32．
∴CM=BN=2,DN=AM=32．
在△ACM与△DBN中，
CM=BN∠AMC=∠BNDAM=DN，
∴△ACM≌△DBN(SAS)，
∴BD=AC，
∴BD+CD=AC+CD．
即：AD=BC；
方法三：当x=0时，y=2；当y=0时，x=32，
∴点C的坐标为(0,2)；点D的坐标为(−32,0)．
∵AD= (xA−xD)2+(yA−yD)2= (32+32)2+(4−0)2= 32+42=5．BC= (xB−xC)2+(yB−yC)2= (3−0)2+(−2−2)2= 32+42=5．
∴AD=BC；
(3)解：∵点C的坐标为(0,2)，点D的坐标为(−32,0)，点A的坐标为点(32,4)，S△PAC=4，
设P(x,0)(x>0)，
∴S△APC=S△APD−S△PDC=12(x+32)×4−12(x+32)×2=x+32，
∴32+x=4，
解得：x=52，
∴P(52,0)．
【解析】(1)将点B(−3,−2)代入反比例函数求得m=6，进而将点A(a,4)，代入y=6x得出A(32,4)，再根据待定系数法求一次函数的解析式即可求解；
(2)方法一：作AM⊥x轴于点M，BN⊥y轴于点N，证明△ADM≌△CBN，根据全等三角形的性质，即可得证；
方法二：作AM⊥y轴于点M，BN⊥x轴于点N，证明△ACM≌△DBN，根据全等三角形的性质，即可得证；
方法三：得出点C的坐标为(0,2)；点D的坐标为(−32,0)，根据勾股定理求得AD，BC，即可得证；
(3)设P(x,0)(x>0)，根据三角形面积列出方程，解方程即可求解．
本题考查了一次函数与反比例函数交点问题，勾股定理，全等三角形的性质与判定，一次函数与坐标轴的交点问题，掌握以上知识是解题的关键．
21.【答案】247
【解析】解：(1)由题意可知，在Rt△CDE中，CE=t，CD=BC−BD=8−t，
∴DE= CD2+CE2= t2+(8−t)2，
∵sin∠EDC=35，
∴CEDE=t t2+(8−t)2=35，即t2t2+(8−t)2=925，
∴(8−tt)2=169，即8−tt=43或8−tt=−43，
解得t=247或t=−8(负值，舍弃)，
故答案为：247；
(2)解：由(1)可知DC=8−t，CE=t，
∵△CDE∽△CAB，
∴CDCA=CECB，
∴8−t6=t8，
∴t=327；
(3)∵y=S△ABC−S△CDE=12CB⋅CA−12CD⋅CE=12×6×8−12t(8−t)=12t2−4t+24=12(t−4)2+16，
∵12>0，开口向上，函数有最小值，
∴当t=4时，y最小值=16．
(1)根据题意，在Rt△CDE中，CE=t，CD=BC−BD=8−t，有勾股定理得到DE= CD2+CE2= t2+(8−t)2，由sin∠EDC=35列方程求解即可得到答案；
(2)由(1)中得到的CE=t，CD=BC−BD=8−t，直接根据△CDE∽△CAB列出比例式求解即可得到答案；
(3)根据题中图形得到y=S△ABC−S△CDE，利用三角形面积公式代值求解y=12(t−4)2+16，再由二次函数性质求出最值即可得到答案．
本题考查三角形背景下动点综合问题，涉及勾股定理、三角函数、相似三角形性质、图形面积及二次函数性质，本题难度不大，综合性强，熟练掌握勾股定理求线段长、三角函数求线段长、相似三角形性质求线段长、图形面积表示及二次函数最值求法是解决问题的关键．
22.【答案】32 5
【解析】(1)证明：过点C作CE/​/AB，交AD的延长线于点E，
∵CE/​/AB，
∴∠E=∠BAE，∠B=∠BCE．
∴△ABD∽△ECD．
∴ABCE=BDCD．
∵AD是△ABC的角平分线，
∴∠BAD=∠CAD．
∴∠E=∠CAD，
∴CA=CE，
∴ABAC=BDCD；
(2)解：∵AD是△ABC的角平分线，
由(1)可得ABAC=BDCD，
∵BDBC=35，
∴BDCD=32，
∴ABAC=BDCD=32．
故答案为：32；
(3)解：延长BE交AD的延长线于点G，
∵四边形ABCD是矩形，
∴AB/​/CD．
∴∠GDE=∠GAB，∠DEG=∠ABG．
∴△GDE∽△GAB，
∴DGAG=DEAB，
∴DG4+DG=13，
∴DG=2．
∴AG=AD+DG=4+2=6，
在Rt△ABG中，∠BAG=90°，
∴BG= AB2+AG2= 32+62=3 5，
∵AF平分∠BAG，
∴BFFG=ABAG=12，
∴BFBG=13，
∴BF= 5．
故答案为： 5．
(1)过点C作CE/​/AB，交AD的延长线于点E，先证明△ABD∽△ECD，得到ABCE=BDCD，接着上述思路，再证明CA=CE，即可得到结论；
(2)AD是△ABC的角平分线，由(1)可得ABAC=BDCD，由BDBC=35得到BDCD=32，即可得到答案；
(3)延长BE交AD的延长线于点G，先证明△GDE∽△GAB，则DGAG=DEAB，求得DG=2，得AG=6，在Rt△ABG中，由勾股定理可得BG=3 5，再根据(1)的结论进一步即可得到答案．
此题主要考查了相似三角形的判定和性质、矩形的性质、勾股定理等知识，熟练掌握相似三角形的判定和性质是解题的关键．
23.【答案】12
【解析】(1)解：由折叠的性质可得∠BDF=∠EDF=90°，S△BDF=S△EDF，BD=ED，
∴∠BDF=∠BCA=90°，
∴DF/​/AC，
∴△BDF∽△BCA，
∴S△BDFS△ABC=(BDBC)2，
∵S△BDFS四边形ACEF=17，
∴S△BDFS△ABC=S△BDFS四边形ACEF+S△BDF+S△EFD=19，
∴BDBC=13，
∴DEDC=12，
故答案为：12；
(2)证明：方法一：∵FE⊥AC，
∴∠AEF=90°．
∴∠C=∠AEF=90°．
∴EF/​/BC，
∴∠CDE=∠FED，
由折叠可知：∠FED=∠B，FB=FE，
∴∠B=∠CDE，
∴DE/​/AB，
∴四边形BDEF是平行四边形．
又∵FB=FE，
∴四边形BDEF是菱形．
方法二：∵FE⊥AC，
∴∠AEF=90°，
∴∠C=∠AEF=90°．
∴EF/​/BC，
∴∠EFD=∠BDF．
由折叠可知：∠BDF=∠EDF，FB=FE，DB=DE．
∴∠EFD=∠EDF．
∴EF=ED．
∴BD=DE=EF=BF．
∴四边形BDEF是菱形．
方法三：∵FE⊥AC，
∴∠AEF=90°．
∴∠C=∠AEF=90°，
∵EF/​/BC，
∴∠FED=∠CDE．
由折叠可知：∠FED=∠B，FB=FE，DE=DB．
∴∠B=∠CDE
∴DE/​/AB，
∴四边形BDEF是平行四边形．
连接BE，
∵FB=FE，DE=DB，
∴点D，F都在BE的垂直平分线上．
∴DF⊥BE
∴四边形BDEF是菱形．
方法四：连接BE，交DF于点O，
∵FE⊥AC，
∴∠AEF=90°．
∴∠C=∠AEF=90°，
∴EF/​/BC，
∴∠DBE=∠FEB
由折叠可知：FB=FE，DE=DB
∴∠DEB=∠DBE.点D，F都在BE的垂直平分线上．
∴DF⊥BE，∠DEB=∠FEB．
∴∠EOF=∠EOD=90°．
∴△EOF≌△EOD．
∴EF=ED．
∴BD=DE=EF=BF．
∴四边形BDEF是菱形．
(3)解：∵EF平分∠AED，
∴∠AEF=∠DEF．
由折叠可知：FB=FE，∠B=∠DEF．
∴∠AEF=∠B．
又∵∠A=∠A，
∴△AEF∽△ABC
∴AEAB=AFAC=EFBC．
∴AE5=AF3=5−AF4．
∴AF=157，AE=257．
∴CE=AE−AC=257−3=47．
(1)根据折叠的性质得到∠BDF=∠EDF=90°，S△BDF=S△EDF，BD=ED，证明△BDF∽△BCA，得到S△BDFS△ABC=(BDBC)2，再由S△BDFS四边形ACEF=17，推出BDBC=13，则DEDC=12；
(2)方法一：先证明EF/​/BC，再证明∠B=∠CDE，得到DE/​/AB，则四边形BDEF是平行四边形．再由FB=FE，即可证明四边形BDEF是菱形；方法二：先证明EF/​/BC，得到∠EFD=∠BDF.再证明∠EFD=∠EDF.推出BD=DE=EF=BF，即可证明四边形BDEF是菱形；方法三：同方法一证明四边形BDEF是平行四边形．连接BE，证明点D，F都在BE的垂直平分线上．得到DF⊥BE，则四边形BDEF是菱形；方法四：连接BE，交DF于点O，先证明EF/​/BC，得到∠DBE=∠FEB，再证明点D，F都在BE的垂直平分线上．得到DF⊥BE，∠DEB=∠FEB.证明△EOF≌△EOD，进而推出BD=DE=EF=BF，即可证明四边形BDEF是菱形；
(3)证明△AEF∽△ABC得到AEAB=AFAC=EFBC.求出AF=157，AE=257.则CE=AE−AC=257−3=47．
本题主要考查了折叠的性质，相似三角形的性质与判定，菱形的判定，全等三角形的性质与判定，线段垂直平分线的性质与判定等等，熟知相似三角形的性质与判定条件是解题的关键．
24.【答案】解：(1)由y=−12x2+x+4得，
当x=0时，y=4，
∴点C的坐标为(0,4)；
当y=0时，−12x2+x+4=0，解得：x1=−2，x2=4．
∵点A在点B的左侧，
∴点A的坐标为(−2,0)，点B的坐标为(4,0)．
∴点D的坐标为(1,92)．
(2)作PM⊥x轴于点M，则∠PMG=90°，

∴∠FOG=∠PMG=90°．
又∵∠FGO=∠PGM．
∴△FGO∽△PGM，
∴FGPG=OPPM．
∴65=3PM
∴PM=52．
当y=52时，−12x2+x+4=52，
∴x1=−1(舍去)，x2=3，
∴m=3，
∴点P的坐标为(3,52)．
(3)存在点P，使得∠FHE=135°，理由如下：
∵∠FHE=135°，
∴∠EHG=45°，
∵∠HEG=90°，
∴∠EGF=45°，
∵∠GOF=90°，
∴∠OFG=45°，
∴∠OFG=∠OGF=45°，
∴OG=OF，
∵F(0,−3)，
∴OF=3，
∴OG=3，
∴G(3,0)，
设直线FG的解析式为y=kx+b，
把G(3,0)，F(0,−3)代入y=kx+b得：3k+b=0b=−3，
∴k=1b=−3，
∴y=x−3，
∴y=x−3y=−12x2+x+4，
∴−12x2+x+4=x−3，
∴x=± 14，
∵点P是第一象限内且在对称轴右侧二次函数图象上的一个动点，点P的横坐标为m，
∴m= 14．
故存在点P，使得∠FHE=135°，m的值为： 14．
【解析】(1)利用函数解析式求出当x=0时，y=4；当y=0时，x1=−2，x2=4；以及顶点坐标公式，即可得出答案；
(2)作PM⊥x轴于点M，通过证明△FGO∽△PGM可得出：FGPG=OPPM.即可得出PM=52.当y=52时，求出x1=−1(舍去)，x2=3，即可得出点P的坐标．
(3)由∠FHE=135°，可得∠EHG=45°，故∠EGF=45°，∠OFG=45°，可得OG=OF=3，即可得出设直线FG的解析式为：y=x−3，结合y=x−3y=−12x2+x+4，即可得出m的值．
本题考查了二次函数的性质，二次函数与相似三角形、特殊角的存在性问题，掌握二次函数的性质，灵活构造图形是解题的关键．