新教材2024版高中数学第四章数列章末素养提升课件新人教A版选择性必修第二册

这是一份新教材2024版高中数学第四章数列章末素养提升课件新人教A版选择性必修第二册，共60页。

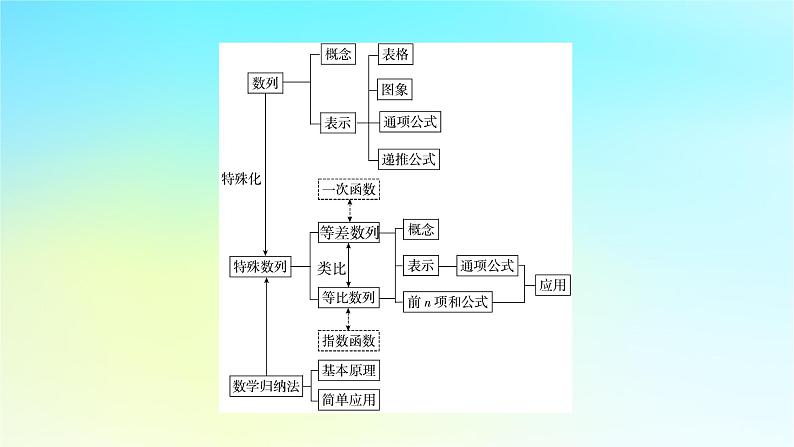
第四章　数列章末素养提升体系构建核心归纳思想方法专题一　方程思想数列是特殊的函数，用函数的观点认识数列和处理数列问题，既有利于理解和掌握数列的基本概念和性质，又有利于解决问题．等差(比)数列的通项公式和求和公式中的五个量中，已知其中任意三个，通过解方程可求其余两个． 设递增等差数列{an}的前n项和为Sn，已知a3＝1，a4是a3和a7的等比中项．(1)求数列{an}的通项公式；(2)求数列{an}的前n项和Sn.【分析】(1)由已知条件列方程组求出{an}的公差，再结合a3＝1，由此能求出an.(2)利用等差数列的前n项和公式求解．【点评】本题考查等差数列的性质和应用，是基础题．解题时要认真审题，仔细解答，注意合理地利用方程思想．【答案】D 专题二　分类讨论思想在解决数学问题时，应注意问题的层次性，即考虑到问题的方方面面，在讨论时应考虑全面，做到不重不漏，这是历年高考的重点．【分析】(1)运用等差数列的通项公式与求和公式，根据条件列方程，求出首项和公差，得到通项an.运用n＝1时，b1＝T1，n＞1时，bn＝Tn－Tn－1，求出bn.(2)写出cn，然后运用分组求和，一组为等差数列，一组为等比数列，分别应用求和公式化简即可．【点评】本题主要考查等差数列和等比数列的通项与求和公式的运用，第(1)问求bn时分n＝1和n≥2讨论；第(2)问求{cn}的前n项和时分n为奇数和偶数两种情况讨论．解：(1)∵an＝an－1·3n－1，两边取以3为底的对数得log3an＝log3an－1＋(n－1)，∴log3an－log3an－1＝n－1，∴log3a2－log3a1＝1，log3a3－log3a2＝2，…，log3an－log3an－1＝n－1，以上各式相加得专题三　转化与化归思想【分析】(1)利用已知条件及等差数列的性质求出数列{an}的公差，由此即可得{an}的通项公式．利用bn＝Sn－Sn－1求{bn}的通项公式，注意分n＝1和n≥2两种情况讨论；(2)先求cn的通项公式，再利用错位相减法求和．【点评】在数列求和时，若题目考查的是非等差(等比)数列，无法使用公式法求和时，就需要利用转化与化归思想，用分组转化法、裂项相消法、错位相减法等方法来求和．素养提升素养一　数学运算——数列基本量中的学科素养在解决数列问题中，常常涉及基本量的运算，需要确定运算对象和运算法则，明确运算方向，能够用程序化的思想理解与表达问题，采取不同的运算方法，体现了数学运算的核心素养．(一)等差数列中的运算素养例1 已知等差数列{an}的前9项和为27，a10＝8，则a100＝ (　　)A．100　　 B．99C．98　　 D．97【答案】C【分析】利用等差数列的前n项和以及等差数列的性质求出公差，再利用等差数列通项公式求解．【点评】本题考查的是等差数列的性质，熟练掌握等差数列的性质，是解答的关键．例2 已知等差数列{an}的前n项和为Sn，且a1＝－11，a5＋a6＝－4，则Sn取得最小值时n的值为 (　　)A．6　　　 B．7C．8　　　 D．9【答案】A【分析】求出Sn的表达式，根据表达式是二次函数，结合二次函数图象的性质求解．【点评】本题综合考查了等差数列与二次函数，借助二次函数求解最值问题．(二)等比数列中的运算素养例3 已知等比数列{an}的公比大于1，Sn为数列{an}的前n项和．已知S3＝7，且a1＋3，3a2，a3＋4构成等差数列，求数列{an}的通项公式．由题意得q>1，∴q＝2，∴a1＝1.故数列{an}的通项为an＝2n－1.【分析】先列方程组求出{an}的公比，再用等比数列的通项公式求解．【点评】对于等差数列与等比数列的综合题，要找准某结合点，弄清哪些是等差数列中的量，哪些是等比数列中的量，注意它们的区别，避免用错公式．素养二　数学抽象和逻辑推理的学科素养数学抽象是最核心的数学素养，是形成理性的重要基础；逻辑推理是要得到数学结论，提出或者验证数学命题的思维过程．数学研究对象的确立依赖于数学抽象，而数学内部自身的发展依赖于数学推理，数列中的观察、归纳得到结论是典型的逻辑推理．例4 (2021年绵阳期中)已知等差数列1，3，5，7，9，11，…，按如下方法分组：(1)，(3，5)，(7，9，11)，(13，15，17，19)，…，则第n组中各数之和为__________．【答案】n3【分析】先由题设求出等差数列的公差，再根据分组的规律求出第n组中各数之和．【点评】解题的关键是看清题目中所给的数列的项与项数之间的关系，注意运算过程不要出错．【分析】(1)直接由已知等式归纳得结论；(2)验证n＝1时结论成立；归纳假设n＝k时结论成立，利用归纳假设证明n＝k＋1时结论成立，最后下结论．【点评】归纳、猜想、证明属于探索性问题的一种，一般经过计算、观察、归纳，然后猜想出结论，再用数学归纳法证明．由于“猜想”是“证明”的前提和“对象”，务必保证猜想的正确性，同时必须注意数学归纳法步骤的书写．素养三　数学建模的核心素养数学建模的过程包括：提出问题、建立模型、求解模型、检验结果、完善模型．能够在熟悉的实际情境中，运用数学思维进行分析，发现情境中的数学关系，提出数学问题；能够运用数学建模的一般方法和相关知识，创造性地建立数学模型，解决问题；能够理解数学建模的意义和作用．例6 (2021年恩施期中)某工厂2019年初有资金1000万元，资金年平均增长率可达到20%，但每年年底要扣除x(x<200)万元用于奖励优秀职工，剩余资金投入再生产．(1)以第2019年为第一年，设第n年初有资金an万元，用an和x表示an＋1，并证明数列{an－5x}为等比数列；(2)为实现2029年初资金翻两番的目标，求x的最大值(精确到万元)．(参考数据：1.29≈5.160，1.210≈6.192，1.211≈7.430)【分析】(1)根据题意可以得出an与an＋1的关系，构造新数列{an－5x}，用等比数列的定义证明；(2)2029年初资金翻两番，表示的也就是经过11年资金达到4000万，即a11≥4000.例7 返乡创业的大学生一直是人们比较关注的对象，他们从大学毕业，没有选择经济发达的大城市，而是回到自己的家乡，为养育自己的家乡贡献自己的力量，在享有“国际花园城市”称号的温江幸福田园，就有一个由大学毕业生创办的农家院“小时代”，其独特的装修风格和经营模式，引来无数人的关注，带来红红火火的现状，给青年大学生们在就业创业上很多新的启示．在接受采访中，该农家院老板谈起以下情况：初期投入为72万元，经营后每年的总收入为50万元，第n年需要付出房屋维护和工人工资等费用是首项为12，公差为4的等差数列{an}(单位：万元)．【分析】(1)运用等差数列的通项公式，代入可求an；(2)根据条件求第n年总盈利的表达式，利用二次函数知识求解最值；(3)根据条件求年平均获利表达式，用基本不等式求最值．链接高考例1.(2020年新课标Ⅰ)设{an}是等比数列，且a1＋a2＋a3＝1，a2＋a3＋a4＝2，则a6＋a7＋a8＝ (　　)A．12 B．24C．30 D．32【答案】D【解析】{an}是等比数列，且a1＋a2＋a3＝1，则a2＋a3＋a4＝q(a1＋a2＋a3)＝2，解得q＝2，所以a6＋a7＋a8＝q5(a1＋a2＋a3)＝25×1＝32.【分析】根据等比数列的性质即可求出．【点评】本题考查了等比数列的性质和通项公式，属于基础题．数列基本量的计算【答案】B【分析】根据等比数列的通项公式求出首项和公比，再根据求和公式即可求出．【点评】本题考查了等比数列的通项公式和求和公式，考查了运算求解能力，属于基础题．【点评】本题考查等差数列的通项公式与前n项和公式的应用，属于基础题．例4.(2020年新课标Ⅱ)记Sn为等差数列{an}的前n项和．若a1＝－2，a2＋a6＝2，则S10＝________．【答案】25【分析】由已知结合等差数的性质及求和公式即可直接求解．【点评】本题主要考查了等差数列的性质及求和公式，属于基础题．例5.(2021年高考甲卷)记Sn为等比数列{an}的前n项和．若S2＝4，S4＝6，则S6＝ (　　)A．7 B．8C．9 D．10【答案】A【解析】∵Sn为等比数列{an}的前n项和，∴S2，S4－S2，S6－S4成等比数列，∴S2＝4，S4－S2＝6－4＝2，∴S6－S4＝1，∴S6＝1＋S4＝1＋6＝7.数列的综合问题【分析】根据题目条件可得S2，S4－S2，S6－S4成等比数列，从而求出S6－S4＝1，进一步求出答案．【点评】本题考查等比数列及其性质的综合，考查分析问题与解决问题的能力，属于中档题．例6.(2020年新课标Ⅱ)北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层．上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块．下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块．已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石) (　　)A．3699块　　 B．3474块C．3402块　　 D．3339块【答案】C【分析】由题意可得从内到外每环之间构成等差数列，且公差d＝9，a1＝9，根据等差数列的性质即可求出n＝9，再根据前n项和公式即可求出．【点评】本题考查了等差数列在实际生活中的应用，考查了分析问题与解决问题的能力，属于中档题．例7.(2020年海南)将数列{2n－1}与{3n－2}的公共项从小到大排列得到数列{an}，则{an}的前n项和为________．【答案】3n2－2n【分析】首先判断{an}是以1为首项，6为公差的等差数列，再利用求和公式，得出结论．【点评】本题考查了等差数列的应用及求和公式，属于基础题．数列求和解：(1)由题设可得b1＝a2＝a1＋1＝2，b2＝a4＝a3＋1＝a2＋2＋1＝5，又因为a2k＋2＝a2k＋1＋1，a2k＋1＝a2k＋2(k∈N*)，【分析】(1)根据题设中的递推关系可得bn＋1＝bn＋3，从而可求{bn}的通项；(2)根据题设中的递推关系可得{an}的前20项和为S20可化为S20＝2(b1＋b2＋…＋b9＋b10)－10，利用(1)的结果可求S20.【点评】对于数列的交叉递推关系，我们一般利用已知的关系得到奇数项的递推关系或偶数项的递推关系，再结合已知数列的通项公式、求和公式等来求解问题．【分析】(1)利用等差数列的性质及a1得到9q2－6q＋1＝0，解方程即可；(2)利用公式法、错位相减法分别求出Sn，Tn，再作差比较即可．【点评】本题主要考查数列求和，涉及等差数列的性质、错位相减法求数列的和，考查学生的数学运算能力，属于中档题．