新教材2024版高中数学第五章一元函数的导数及其应用章末素养提升课件新人教A版选择性必修第二册

这是一份新教材2024版高中数学第五章一元函数的导数及其应用章末素养提升课件新人教A版选择性必修第二册，共60页。

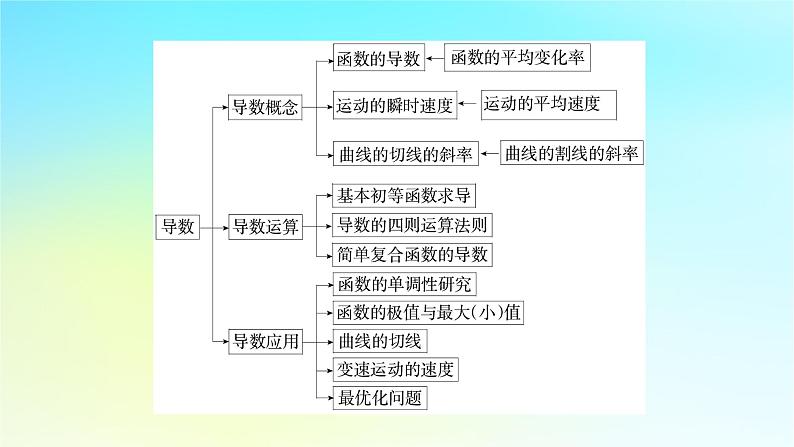
第五章　一元函数的导数及其应用章末素养提升体系构建核心归纳思想方法专题一　数形结合思想数形结合的思想，其实质是将抽象的数学语言与直观的图象结合起来，关键是代数问题与图形之间的相互转化，它可以使代数问题几何化，几何问题代数化．已知函数f(x)＝x3＋3ax－1，g(x)＝f′(x)－ax－5，其中f′(x)是f(x)的导函数．(1)对满足－1≤a≤1的一切a的值，都有g(x)<0，求实数x的取值范围；(2)设a＝－m2，当实数m在什么范围内变化时，函数y＝f(x)的图象与直线y＝3只有一个公共点．②当m≠0时，f′(x)＝3x2－3m2＝0，得x＝±|m|，列表如下f(x)极小＝f(|m|)＝－2m2|m|－1<－1.又因为f(x)的值域是R，且在(|m|，＋∞)上单调递增，所以当x>|m|时，函数y＝f(x)的图象与直线y＝3只有一个公共点．【点评】对于函数交点问题，我们可以应用导数讨论根的情况：首先，由导数研究出相应函数的单调性、极值(最值)，并结合解析式分析出函数图象的变化趋势；其次，由函数的性质(单调性、极值、奇偶性等)和变化趋势画出函数的示意图；最后，根据图象与x轴的交点情况，确定参数的取值范围．【答案】D【解析】如图，由f(x)＝ax－|ln x|＋1有三个不同的零点，可得y＝ax＋1与y＝|ln x|的图象有三个交点，画出函数y＝|ln x|的图象，直线y＝ax＋1过定点(0，1)，当x>1时，设过点(0，1)的直线与y＝ln x的切点为(x0，ln x0).专题二　分类与整合思想分类与整合是重要的数学解题思想．它把数学问题划分成若干个局部问题，在每一个局部问题中，原先的“不确定因素”不再影响问题的解决，当这些局部问题都解决时，整个问题也就解决了．实质上分类讨论是“化整为零，各个击破，再合零为整”的解题策略．引起讨论的主要原因有：①参数对函数类型、导函数的符号、单调区间端点的不同影响；②函数分段；③不等式两边同时乘(除以)某因式时，此因式的符号；④等式变形时除以(乘)某因式时，因式是否为零；⑤数值的大小关系等．导数中的含参数的讨论分四级：一级：最高次项的系数含参数a，分a＝0，a>0，a<0三种情况依次讨论该系数．“a＝0”时，写出不含参数的f′(x)的最简洁、直观的形式；“a>0”或“a<0”时，把最高次项系数外提，化简变形(含因式分解)到最简洁、直观的形式，能直接看出根来．二级：接一级，判断方程f′(x)＝0是否有根，即分Δ＝0，Δ>0，Δ<0三种情况讨论．如果方程f′(x)＝0没有实根，说明f′(x)>0或f′(x)<0恒成立，即f(x)单调递增或单调递减，直接写结论；如果方程f′(x)＝0有实根，求出所有的根，然后进入级别三．三级：接二级，判断得出的根是否在定义域内．①若f′(x)＝0的根不在定义域内，则f′(x)>0或f′(x)<0，说明函数f(x)在定义域内单调递增或单调递减，直接写出结论；②若f′(x)＝0有一个根在定义域内，则对这个唯一的根进行列表，求出f(x)的单调递增区间和单调递减区间；③若f′(x)＝0在定义域内有两根(包含两等根或两异根)，那么就进入四级．四级：接三级，在三级中确定f′(x)＝0在定义域内有两根x1，x2的情况下，讨论两根的大小．【点评】本题重点考查通过求导研究函数的单调性，本题主要的数学思想是分类讨论，即对两根大小进行讨论．分类要做到不重不漏，层次分明．【答案】D专题三　转化化归思想等价转化是把未知的问题转化为在已有知识范围内可解的问题的一种重要的思想方法．通过不断的转化，把不熟悉、复杂的问题转化为熟悉甚至模式化、简单化的问题．不断培养和训练转化意识，将有利于强化解决数学问题中的应变能力，提高思维能力和技能、技巧．【分析】本题考查恒成立问题，通过对问题的挖掘，实际上是求函数的最值问题，借助导数工具以及不等式恒成立结论解决．【点评】解决本题的关键是转化思想的应用，求参数k的范围问题转化为求函数的最值问题，再通过求最值转化为解不等式解决．利用导数求函数最值是解决不等式恒成立问题的一种重要方法．“构造”是一种重要而灵活的思维方式，应用好构造思想解题的关键是：一要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行逻辑组合．【答案】A素养提升素养一　导数的运算素养数学运算要求能够在关联的情境中确定运算对象，提出运算问题．能够针对运算问题，合理选择运算方法、设计运算程序，解决问题．能够理解运算是一种演绎推理；能够在综合利用运算方法解决问题的过程中，体会程序化思想的意义和作用．在交流的过程中，能够借助运算探讨问题．导数中涉及运算、求导以及求导后研究函数的性质．【答案】B【点评】本题考查拉格朗日中值定理、函数的零点与方程的根的应用，考查理解辨析能力与运算求解能力，解决问题关键是利用定义结合导数的运算进行求解．例2　在许多实际问题中，一个因变量往往与几个自变量有关，即因变量的值依赖于几个自变量，这样的函数称为多元函数．例如，某种商品的市场需求量不仅仅与其市场价格有关，而且与消费者的收入以及这种商品的其他代用品的价格等因素有关，即决定该商品需求量的因素不止一个而是多个．我们常常用偏导数来研究多元函数．以下是计算二元函数z＝f(x，y)＝2x2＋y＋3xy2在(1，2)处偏导数的全过程：fx′(x，y)＝4x＋3y2，fy′(x，y)＝1＋6xy，所以fx′(1，2)＝4×1＋3×22＝16，fy′(1，2)＝1＋6×1×2＝13.由上述过程，二元函数z＝g(x，y)＝ln(x2＋y2)，则gx′(1，2)＋gy′(1，2)＝__________.【点评】本题主要考查归纳推理与导数的计算，解题关键是看懂新定义中计算偏导数的过程．素养二　导数中的逻辑推理能够跟已学过的知识有关联的数学命题，通过对条件与结果的分析，探索论证的思路，选择合适的论证方法予以证明，并能用准确的数学语言表述论证过程；能够通过举反例说明某些数学结论不成立．导数中的推理证明问题主要是通过构造函数，利用导数证明函数的单调性．【思路点拨】求出f(x)＝g(ex)，得到g(n)＝f(m)＝g(em)，求出m＝ln n，则mn＝n·ln n，n∈(0，1)，令h(x)＝xln x，x∈(0，1)，根据函数的单调性求出h(x)的最小值即mn的最小值即可．【点评】本题考查了函数的单调性、最值问题，考查导数的应用以及转化思想，是一道常规题．【思路分析】(1)f(x)＝(x＋3)ex－3，定义域为R，求导，分析单调性，进而得函数f(x)的最值；(2)问题可以转化为，当x≥0时，(x＋1)ex－(mx2＋2x＋1)≥0恒成立，令g(x)＝(x＋1)ex－(mx2＋2x＋1)，只需要g(x)min≥0即可，接下来分类讨论求g(x)min即可．【点评】本题考查利用导数研究函数的单调性和极值，理解函数的单调性与导数的正负性之间的联系是解题的关键，考查学生的逻辑推理能力和运算能力．链接高考【答案】5x－y＋2＝0导数的几何意义的应用【分析】先验证点在曲线上，再求导，代入切线方程公式即可．【点评】本题考查利用导数研究过曲线上某点处的切线方程，是基础的计算题．【答案】D【点评】本题考查直线与圆的位置关系，属于基础题，采用选项检验，排除思想解题，有时事半功倍．例3.(2019年新课标Ⅱ)曲线y＝2sin x＋cos x在点(π，－1)处的切线方程为 (　　)A．x－y－π－1＝0 B．2x－y－2π－1＝0C．2x＋y－2π＋1＝0 D．x＋y－π＋1＝0【答案】C【解析】由y＝2sin x＋cos x，得y′＝2cos x－sin x，∴y′|x＝π＝2cos π－sin π＝－2，∴曲线y＝2sin x＋cos x在点(π，－1)处的切线方程为y＋1＝－2(x－π)，即2x＋y－2π＋1＝0.【分析】求出原函数的导函数，得到函数在x＝π时的导数，再由直线的点斜式方程得答案．【点评】本题考查利用导数研究过曲线上某点处的切线方程，熟记基本初等函数的导函数是关键，属于基础题．例4.已知曲线y＝aex＋xln x在点(1，ae)处的切线方程为y＝2x＋b，则 (　　)A．a＝e，b＝－1 B．a＝e，b＝1C．a＝e－1，b＝1 D．a＝e－1，b＝－1【答案】D【解析】y＝aex＋xln x的导数为y′＝aex＋ln x＋1，在点(1，ae)处的切线方程为y＝2x＋b，可得ae＋1＋0＝2，解得a＝e－1，又因为切点为(1，1)，可得1＝2＋b，即b＝－1.【分析】求得函数y的导数，可得切线的斜率，由切线方程，可得ae＋1＋0＝2，可得a，进而得到切点，代入切线方程可得b的值．【点评】本题考查导数的运用：求切线的斜率，考查直线方程的运用，考查方程思想和运算能力，属于基础题．例5.(2020年新课标Ⅰ)曲线y＝ln x＋x＋1的一条切线的斜率为2，则该切线的方程为____________．【答案】y＝2x【分析】求得函数y＝ln x＋x＋1的导数，设切点为(m，n)，可得切线的斜率，解方程可得切点，进而得到所求切线的方程．【点评】本题考查导数的运用：求切线的方程，考查直线方程的运用，考查方程思想和运算能力，属于基础题．【答案】1导数的运算【点评】本题主要考查求函数的导数，属于基础题．导数的实际应用【点评】本题考查函数在实际问题中的应用，考查利用导数求最值的应用，考查运算能力和分析问题与解决问题的能力，属于中档题．8. (2021年新高考Ⅰ)函数f(x)＝|2x－1|－2ln x 的最小值为________．导数研究函数的极值、最值等综合性问题例【点评】本题考查利用导数研究函数的单调性和最值，以及运算能力，属于中档题．【分析】(1)(ⅰ)根据导数的几何意义即可求出切线方程；(ⅱ)根据导数和函数单调性极值的关系，即可求出．(2)要证不等式成立，只要证明(x1－x2)[f′(x1)＋f′(x2)]－2[f(x1)－f(x2)]>0，根据导数和函数最值的关系，以及放缩法即可证明．【点评】本题考查利用导数研究函数的单调性、极值，对不等式进行证明，属于难题．