新教材适用2023_2024学年高中数学第8章立体几何初步习题课课件新人教A版必修第二册

这是一份新教材适用2023_2024学年高中数学第8章立体几何初步习题课课件新人教A版必修第二册，共37页。

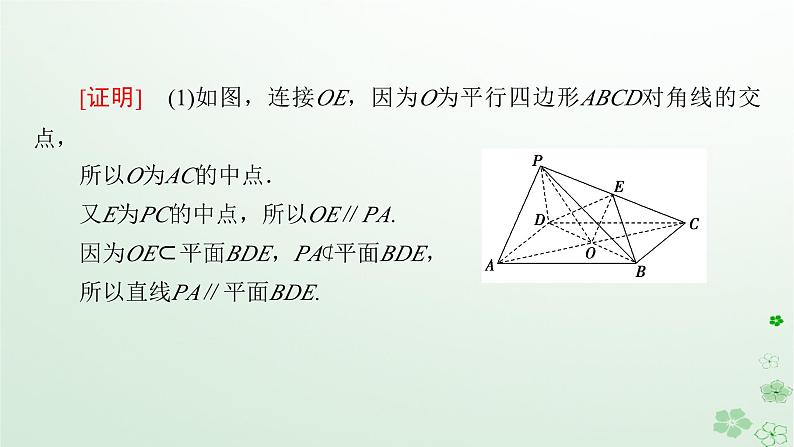
第八章　立体几何初步习题课　平行与垂直的综合问题关键能力•攻重难 如图，在四棱锥P－ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP＝OC，PA⊥PD.求证：(1)直线PA∥平面BDE；(2)平面BDE⊥平面PCD.题|型|探|究[证明]　(1)如图，连接OE，因为O为平行四边形ABCD对角线的交点，所以O为AC的中点．又E为PC的中点，所以OE∥PA.因为OE⊂平面BDE，PA⊄平面BDE，所以直线PA∥平面BDE.(2)因为OE∥PA，PA⊥PD，所以OE⊥PD.因为OP＝OC，E为PC的中点，所以OE⊥PC.又PD⊂平面PCD，PC⊂平面PCD，PC∩PD＝P，所以OE⊥平面PCD.因为OE⊂平面BDE，所以平面BDE⊥平面PCD.[归纳提升]　(1)在应用线面平行的判定定理进行平行转化时，一定注意定理成立的条件，通常应严格按照定理成立的条件规范书写步骤，如：把线面平行转化为线线平行时，必须说清经过已知直线的平面和已知平面相交，这时才有直线与交线平行．(2)对于有关两个平面垂直的证明，一般利用两个平面垂直的判定定理：如果一个平面经过另一个平面的垂线，那么这两个平面垂直，在应用定理解决问题时，经常采取“线线垂直”⇒“线面垂直”⇒“面面垂直”的转化思想进行推理．(1)BG∥平面ACD；(2)平面BCG⊥平面GDE.(2)因为△ACD为等腰三角形，且AC＝AD，又点F为CD的中点，所以AF⊥CD,因为DE⊥平面ACD，AF⊂平面ACD，所以DE⊥AF,因为CD∩DE＝D，CD，DE⊂平面CDE，所以AF⊥平面CDE,由(1)知AF∥BG，所以BG⊥平面CDE，因为BG⊂平面BCG，所以平面BCG⊥平面CDE，又平面CDE即是平面GDE，所以平面BCG⊥平面GDE.(1)求证：BC⊥平面ACD；(2)点F在棱CD上，且满足AD∥平面BEF，求几何体F－BCE的体积．[归纳提升]　平面图形翻折为空间图形问题的解题关键是看翻折前后线面位置关系的变化，根据翻折的过程找到翻折前后线线位置关系中没有变化的量和发生变化的量，这些不变的和变化的量反映了翻折后的空间图形的结构特征．解决此类问题的步骤为： (2023·安徽阜阳期末)如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△CDF折起，使点C到达点P 的位置，且平面PEF⊥平面ABFD.(1)证明：PF⊥PE；(2)若AB＝2，求三棱锥B－PEF的体积．[解析]　(1)证明：因为四边形ABCD为正方形，E，F分别为AD，BC的中点，所以BF⊥EF，又平面PEF⊥平面ABFD，且平面PEF∩平面ABFD＝EF，BF⊂平面ABFD，所以BF⊥平面PEF，所以BF⊥PF.又因为BF∥AD，所以PF⊥AD.又PF⊥PD，AD∩PD＝D，所以PF⊥平面ADP，又PE⊂平面ADP，所以PF⊥PE.(2)当P为AM的中点时，MC∥平面PBD.理由如下：如图，连接AC交BD于O.因为四边形ABCD为矩形，所以O为AC的中点．连接OP，因为P为AM的中点，所以MC∥OP.又MC⊄平面PBD，OP⊂平面PBD，所以MC∥平面PBD.[归纳提升]　探索性问题的一般解题方法先假设其存在，然后把这个假设作为已知条件，和题目的其他已知条件一起进行推理论证和计算．在推理论证和计算无误的前提下，如果得到了一个合理的结论，则说明存在；如果得到了一个不合理的结论，则说明不存在． (2023·福建莆田一中期中)如图，在四棱锥P－ABCD中，PA⊥平面ABCD，在直角梯形ABCD中，AD∥BC，∠BAD＝90°，BC＝2AD，E为线段BC的中点．(1)求证：平面PDE⊥平面PAD；(2)在线段PB上找一点F，使得EF∥平面PCD，则满足题意的点F 是否存在？若存在，求出点F的位置；若不存在，请说明理由；(3)若Q是PC的中点，AB＝1，PA＝2，BC＝2，求三棱锥P－ABQ的体积．[解析]　(1)证明：∵AD∥BC，BC＝2AD，E是BC的中点，∴AD∥BE，AD＝BE，∴四边形ABED是平行四边形，∵∠BAD＝90°，∴四边形ABED为矩形，∴DE⊥AD.∵PA⊥平面ABCD，DE⊂平面ABCD，∴PA⊥DE，又AD∩PA＝A，∴DE⊥平面PAD，又DE⊂平面PDE，∴平面PDE⊥平面PAD.(2)取PB的中点F，连接EF.在△BCP中，E，F分别为BC，BP的中点，∴EF∥CP，又CP⊂平面PCD，EF⊄平面PCD，∴EF∥平面PCD，∴当F为PB的中点时，EF∥平面PCD.课堂检测•固双基1．如图所示，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M，N分别是AB，PC的中点，PA＝AD＝a.(1)求证：MN∥平面PAD；(2)求证：MN⊥平面PCD.[证明]　(1)如图，取CD的中点E，连接NE，ME.∵E，M，N分别是CD，AB，PC的中点，∴NE∥PD，EM∥DA，NE∩EM＝E且NE，EM⊂平面NEM.∴平面NEM∥平面PDA，∴MN∥平面PAD.2．(2021·全国Ⅰ卷)如图，在三棱锥A－BCD中，平面ABD⊥平面BCD，AB＝AD，O为BD的中点．(1)证明：OA⊥CD；(2)若△OCD是边长为1的等边三角形，点E在棱AD上，DE＝2EA，且二面角E－BC－D的大小为45°，求三棱锥A－BCD的体积．[解析]　(1)证明：在△ABD中，∵AB＝AD，O为BD的中点，∴AO⊥BD，∵平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，AO⊂平面ABD，∴AO⊥平面CBD，CD⊂平面CBD，∴AO⊥CD.(2)过点E作EN∥AO交BD于N，过点N作NM∥CD交BC于M，∴AO⊥平面CBD，EN∥AO，∴EN⊥平面CBD，在△BCD中，∵OB＝OD＝OC＝1，∴∠BCD＝90°，即DC⊥BC，