新教材适用2023_2024学年高中数学第9章统计章末知识梳理课件新人教A版必修第二册

这是一份新教材适用2023_2024学年高中数学第9章统计章末知识梳理课件新人教A版必修第二册，共36页。
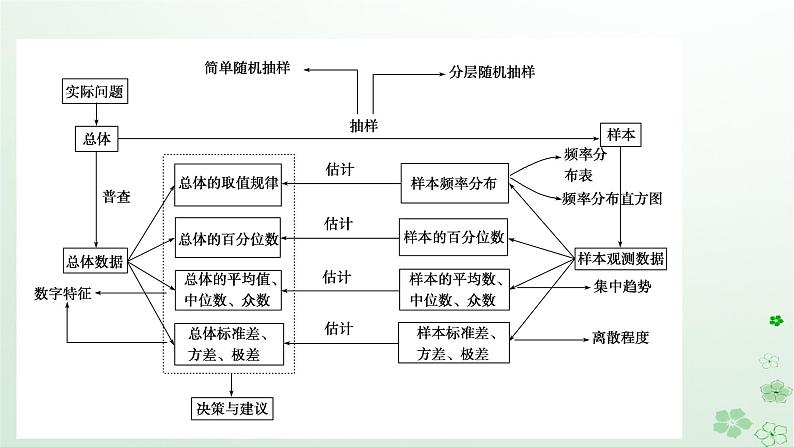
第九章　统计章末知识梳理知识体系构建核心知识归纳一、随机抽样1．简单随机抽样(1)特征：①逐个不放回的抽取；②每个个体被抽到的概率都相等．(2)常用方法：①抽签法；②随机数法．2．分层随机抽样(1)定义：按一个或多个变量把总体划分成若干个子总体，每个个体属于且仅属于一个子总体，在每个子总体中独立地进行简单随机抽样，再把所有子总体中抽取的样本合在一起作为总样本．(3)在比例分配的分层随机抽样中．我们可以直接用样本平均数估计总体平均数．二、用样本估计总体1．频率分布直方图可以利用频率分布直方图估计总体的取值规律．2．百分位数与总体百分位数的估计(1)第p百分位数：一般地，一组数据的第p百分位数是这样一个值，它使得这组数据中至少有p%的数据小于或等于这个值，且至少有(100－p)%的数据大于或等于这个值．(2)可以用样本数据的百分位数估计总体的百分位数．3．众数、中位数和平均数与总体集中趋势的估计4．总体集中趋势的估计要点专项突破1.两种抽样方法的适用范围：当总体容量较小，样本容量也较小时，可采用抽签法；当总体容量较大，样本容量较小时，可采用随机数法；当总体中个体差异较显著时，可采用分层随机抽样．2．掌握两种抽样方法，提升数据分析素养． 为了了解学生学习的情况，某校采用分层随机抽样的方法从高一1 200人、高二1 000人、高三n人中，抽取90人进行问卷调查．已知高一被抽取的人数为36，那么高三被抽取的人数为( )A．20 B．24C．30 D．32[分析]　各层中抽样比例相同．B 某地共有10万户居民，从中随机调查1 000户居民拥有电脑的情况，调查结果如下表：若该地区城市与农村住户之比为4∶6，估计该地区无电脑的农村居民总户数约为( )A．0.923万户 B．1.385万户C．1.8万户 D．1.2万户B与频率分布直方图有关问题的常见类型及解题策略(1)已知频率分布直方图中的部分数据，求其他数据，可利用频率和等于1求解. (2)已知频率分布直方图，求某种范围内的数据，可利用图形及某范围结合求解． 下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位：cm)：(1)列出样本的频率分布表(频率保留两位小数)；(2)画出频率分布直方图；(3)估计身高低于134 cm的人数占总人数的百分比．[解析]　(1)列出样本频率分布表：(2)画出频率分布直方图，如图所示．所以估计身高低于134 cm的人数约占总人数的19%. 某保险公司为客户定制了5个险种：甲，一年期短险；乙，两全保险；丙，理财类保险；丁，参保险种比例定期寿险；戊，重大疾病保险．各种保险按相关约定进行参保与理赔．已知该保险公司对5个险种的参保客户进行抽样调查，得出如上统计图例，则以下四个选项错误的是( )AA．18～29周岁人群参保总费用最少B．30周岁以下的参保人群约占参保人群的20%C．54周岁以上的参保人数最少D．丁险种更受参保人青睐[解析]　由扇形统计图及折线图可知，8%×6 000