数学必修 第二册8.6 空间直线、平面的垂直教课ppt课件

这是一份数学必修 第二册8.6 空间直线、平面的垂直教课ppt课件，共45页。PPT课件主要包含了素养目标•定方向，必备知识•探新知，a⊂α，a⊥l，关键能力•攻重难，题型探究，ACD，拓展应用，课堂检测•固双基等内容，欢迎下载使用。
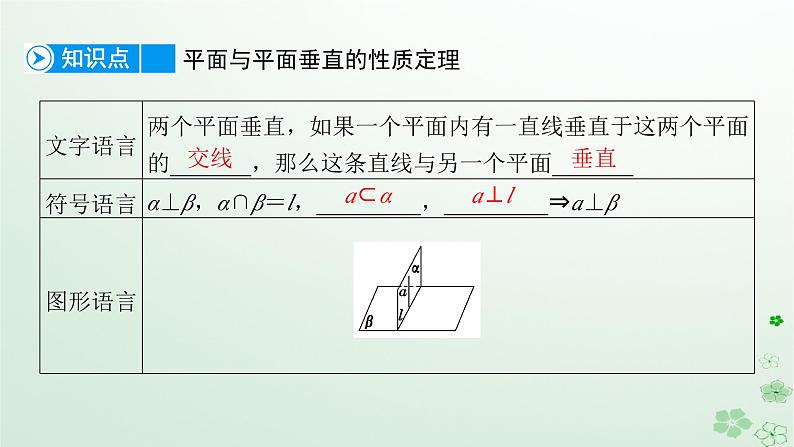
8．6　空间直线、平面的垂直8.6.3　平面与平面垂直第2课时　平面与平面垂直的性质
 1．借助长方体，通过直观感知，归纳出平面与平面垂直的性质定理，并加以证明．2．能用平面与平面垂直的性质定理解决一些简单的空间线面位置关系问题． 在发现、推导和应用平面与平面垂直的性质定理的过程中，发展学生的数学抽象素养、逻辑推理素养和直观想象素养.
[提醒]　对面面垂直的性质定理的理解(1)定理成立的条件有三个：①两个平面互相垂直；②直线在其中一个平面内；③直线与两平面的交线垂直．(2)定理的实质是由面面垂直得线面垂直，故可用来证明线面垂直．(3)已知面面垂直时，可以利用此定理转化为线面垂直，再转化为线线垂直．
[拓展]　平面与平面垂直的其他性质与结论(1)如果两个平面互相垂直，那么经过第一个平面内一点垂直于第二个平面的直线在第一个平面内．即α⊥β，A∈α，A∈b，b⊥β⇒b⊂α.(2)如果两个平面互相垂直，那么与其中一个平面平行的平面垂直于另一个平面．即α⊥β，γ∥β⇒γ⊥α.(3)如果两个平面互相垂直，那么其中一个平面的垂线平行于另一个平面或在另一个平面内．即α⊥β，b⊥β⇒b∥α或b⊂α.(4)如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面．即α∩β＝l，α⊥γ，β⊥γ⇒l⊥γ.(5)三个两两垂直的平面的交线也两两垂直．即α⊥β，α∩β＝l，β⊥γ，β∩γ＝m，γ⊥α，γ∩α＝n⇒l⊥m，m⊥n，l⊥n.
练一练：平面α⊥平面β，α∩β＝l，n⊂β，n⊥l，直线m⊥α，则直线m与n的位置关系是_______.[解析]　因为α⊥β，α∩β＝l，n⊂β，n⊥l，所以n⊥α.又m⊥α，所以m∥n.
(多选题)已知两个平面垂直，下列命题中不正确的是( 　　　 )A．一个平面内的已知直线必垂直于另一个平面内的任意一条直线B．一个平面内的已知直线必垂直于另一个平面的无数条直线C．一个平面内的任一条直线必垂直于另一个平面D．过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面
[解析]　一个平面内只有垂直交线的线和另一个平面垂直，才和另一个平面内任意一条直线垂直，所以A，C错误；因为一个平面内有无数条平行直线垂直于该平面，都与该直线是垂直的，所以B正确；过平面内任意一点作交线的垂线，该垂线在平面内时，则此垂线必垂直于另一个平面，若点在交线上时，作交线的垂线，则垂线不一定在平面内，此垂线不一定垂直于另一个平面．[归纳提升]　对于D，很容易认为是正确的，其实与面面垂直的性质定理是不同的，“两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直”与“两个平面垂直，过一个平面内任意一点作交线的垂线，则此垂线与另一个平面垂直”是不同的，关键是过平面内一点作的直线不一定在平面内．
对于直线m，n和平面α，β，能得出α⊥β的一个条件是( 　　)A．m⊥n，m∥α，n∥βB．m⊥n，α∩β＝m，n⊂αC．m∥n，n⊥β，m⊂αD．m∥n，m⊥α，n⊥β[解析]　对于C选项，在β内取两条相交直线a与b，因为n⊥β，所以n⊥a，n⊥b，又m∥n，所以m⊥a，m⊥b，又a与b相交，所以m⊥β，又m⊂α，所以α⊥β，所以C正确.
[归纳提升]　若所给题目中有面面垂直的条件，一般要利用面面垂直的性质定理将其转化为线面垂直、线线垂直．应用面面垂直的性质定理，注意三点：①两个平面垂直是前提条件；②直线必须在其中一个平面内；③直线必须垂直于它们的交线．
如图，在四棱锥P－ABCD中，侧面PAD是正三角形，且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD＝60°，N是PB的中点，过A，D，N三点的平面交PC于M，E为AD的中点．求证：(1)EN∥平面PDC；(2)BC⊥平面PEB；(3)平面PBC⊥平面ADMN.
又∵E为AD的中点，∴MN∥DE且MN＝DE.∴四边形DENM为平行四边形．∴EN∥DM，且DM⊂平面PDC，EN⊄平面PDC，∴EN∥平面PDC.
(2)∵四边形ABCD是边长为2的菱形，且∠BAD＝60°，∴BE⊥AD.又∵侧面PAD是正三角形，且E为中点，∴PE⊥AD，又∵PE∩BE＝E，∴AD⊥平面PBE.又∵AD∥BC，∴BC⊥平面PEB.
(3)由(2)知AD⊥平面PBE，又PB⊂平面PBE，∴AD⊥PB.又∵PA＝AB，N为PB的中点，∴AN⊥PB.且AN∩AD＝A，∴PB⊥平面ADMN.又∵PB⊂平面PBC.∴平面PBC⊥平面ADMN.
[归纳提升]　垂直关系的转化在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化．每一种垂直的判定都是从某一垂直开始转向另一垂直，最终达到目的，其转化关系如下：
如图，P是正方形ABCD所在平面外一点，且平面PAC⊥平面ABCD，E、F分别是线段AB、PC的中点．(1)求证：EF∥平面PAD；(2)求证：BD⊥PC.
证法三：取CD中点I，连接EI，FI，由于E，F，I均为中点，所以FI∥PD，EI∥AD，FI∩EI＝I，FI，EI⊂平面FIE，PD∩AD＝D，PD，AD⊂平面PAD，平面EFI∥平面PAD，EF⊂平面FIE，所以EF∥平面PAD.
(2)因为正方形ABCD中，BD⊥AC，又平面ABCD⊥平面PAC;平面PAC∩平面ABCD＝AC，BD⊂平面ABCD，所以BD⊥平面PAC，因为PC⊂平面PAC，所以BD⊥PC.
垂直的综合应用 　如图所示，在斜三棱柱A1B1C1－ABC中，底面是等腰三角形，AB＝AC，D是BC的中点，侧面BB1C1C⊥底面ABC.(1)求证：AD⊥CC1；(2)过侧面BB1C1C的对角线BC1的平面交侧棱于点M，若AM＝MA1，求证：截面MBC1⊥侧面BB1C1C；(3)若截面MBC1⊥侧面BB1C1C，则AM＝MA1吗？请叙述你的判断理由．
[分析]　(1)根据面面垂直的性质定理易证AD⊥CC1；(2)先证C1N⊥侧面BB1C1C，根据面面垂直的判定定理即可得证；(3)先证M，E，D，A四点共面，再证四边形AMED是平行四边形，进而即可证明．[解析]　(1)因为AB＝AC，D是BC的中点，所以AD⊥BC.因为底面ABC⊥侧面BB1C1C，底面ABC∩侧面BB1C1C＝BC，所以AD⊥侧面BB1C1C.又CC1⊂平面BB1C1C，所以AD⊥CC1.
(2)证明：延长B1A1与BM交于点N，连接C1N.因为AM＝MA1，所以NA1＝A1B1.因为A1C1＝A1N＝A1B，所以C1N⊥B1C1，所以C1N⊥侧面BB1C1C.所以截面MBC1⊥侧面BB1C1C.
(3)结论正确．证明如下：过M作ME ⊥BC1于点E，连接DE.因为截面MBC1⊥侧面BB1C1C，所以ME⊥侧面BB1C1C，又AD⊥侧面BB1C1C，所以ME∥AD，所以M，E，D，A四点共面．因为MA∥侧面BB1C1C，所以AM∥DE.所以四边形AMED是平行四边形，又AM∥CC1，所以DE∥CC1.
如图，在四棱锥P－ABCD中，底面ABCD为菱形，∠BAD＝60°，PA＝PD＝AD＝2，M，N分别为线段PC，AD的中点．(1)求证：AD⊥平面PBN；(2)若平面PAD⊥平面ABCD，求三棱锥P－NBM的体积．
1．若平面α⊥平面β，平面β⊥平面γ，则( 　　)A．α∥γB．α⊥γC．α与γ相交但不垂直D．以上都有可能
2．(2022·长春高一检测)已知直线a和平面α、β有如下关系：①α⊥β，②α∥β，③a⊥β，④a∥α，则下列命题为真的是( 　　)A．①③⇒④B．①④⇒③C．③④⇒①D．②③⇒④[解析]　由α⊥β，a⊥β，可得a∥α或a⊂α，故A错误；由α⊥β，a∥α，可得a⊂β或a∥β或a与β相交，故B错误；由a∥α，过a作平面γ与α相交，交线为b，则a∥b，因为a⊥β，所以b⊥β，而b⊂α，可得α⊥β，故C正确；由α∥β，a⊥β，可得a⊥α，故D错误．
3．已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则( 　　)A．m∥lB．m∥nC．n⊥lD．m⊥n[解析]　因为α∩β＝l，所以l⊂β，又n⊥β，所以n⊥l.
4．如图所示，三棱锥P－ABC中，平面PAB⊥底面ABC，且PA＝PB＝PC，则△ABC是_______三角形．[解析]　设P在平面ABC上的射影为O，∵平面PAB⊥底面ABC，平面PAB∩平面ABC＝AB，∴O∈AB.∵PA＝PB＝PC，∴OA＝OB＝OC，∴O是△ABC的外心，且是AB的中点，∴△ABC是直角三角形．
5．如图，在直二面角α－AB－β中，AC和BD分别在平面α和β上，它们都垂直于AB，且AB＝4，AC＝6，BD＝8，则CD＝________.