举一反三：六年级数学上册第四单元《比》（2）期末重难点题型（原卷版+解析版）人教版

这是一份举一反三：六年级数学上册第四单元《比》（2）期末重难点题型（原卷版+解析版）人教版，文件包含举一反三六年级数学上册第四单元《比》2期末重难点题型原卷版人教版docx、举一反三六年级数学上册第四单元《比》2期末重难点题型解析版人教版docx等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。

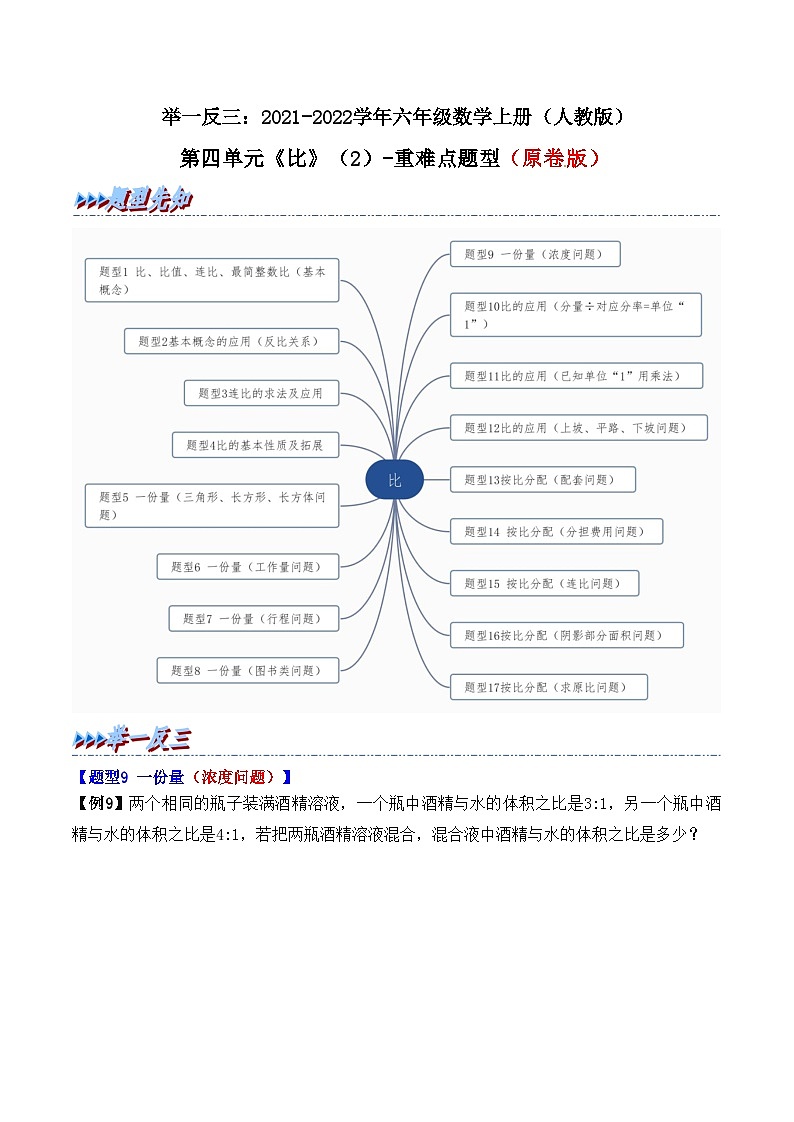
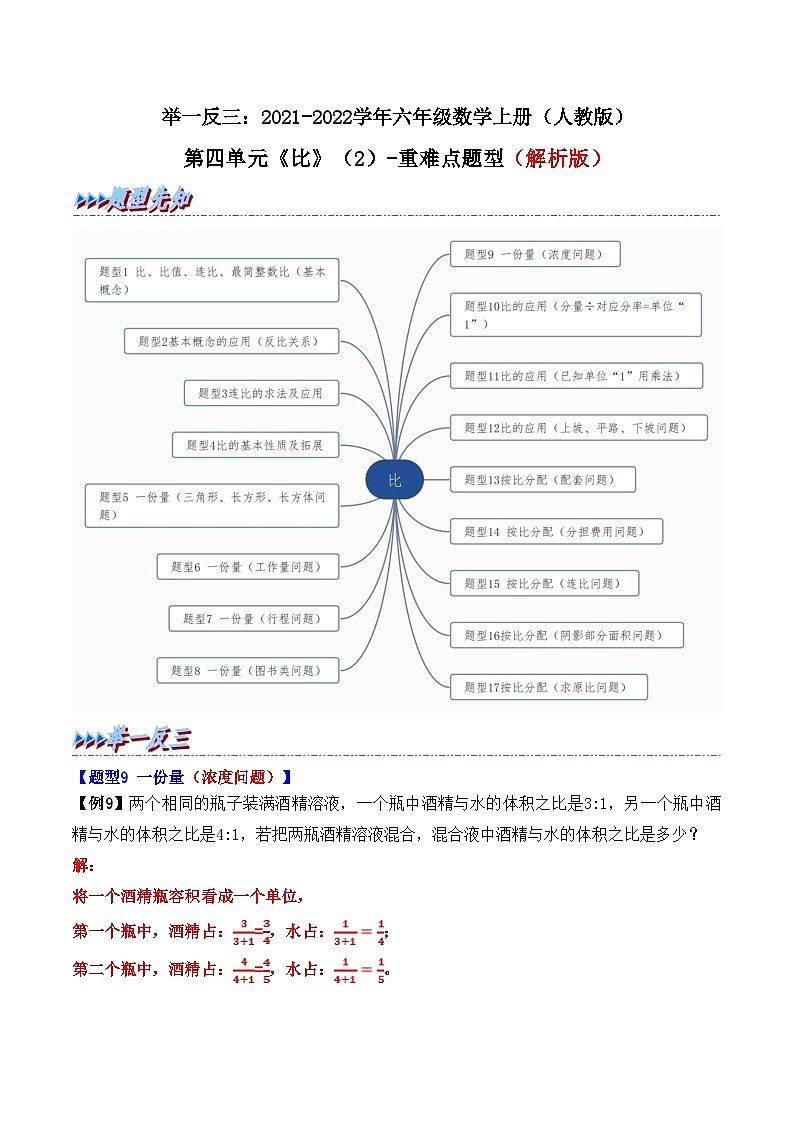
【题型9 一份量（浓度问题）】
【例9】两个相同的瓶子装满酒精溶液，一个瓶中酒精与水的体积之比是3:1，另一个瓶中酒精与水的体积之比是4:1，若把两瓶酒精溶液混合，混合液中酒精与水的体积之比是多少？
解：
将一个酒精瓶容积看成一个单位，
第一个瓶中，酒精占：=，水占：；
第二个瓶中，酒精占：=，水占：。
在混合液中，酒精和水的体积之比是：
（1× + 1×）:（1× + 1×）
=:
=31:9。
答：混合液中酒精和水的体积之比是31:9。
点拨：首先理解两瓶酒精溶液混合后酒精和水的体积没变，所以把一个酒精瓶看成一个单位，分别求出两个瓶子中的酒精、水各占总体的比，再用酒精之和与水的体积之和相比，得到答案。
【变式9-1】两个相同的瓶子都装满酒精溶液，A瓶中酒精与水的体积比是1:2，而B瓶中酒精与水的体积比是1:3。现把两个瓶子中的酒精溶液充分混合，混合液中酒精与水的体积之比是多少？
解：
将一个酒精瓶容积看成一个单位，
第一个瓶中，酒精占：=，水占：；
第二个瓶中，酒精占：=，水占：。
在混合液中，酒精和水的体积之比是：
（1× + 1×）:（1× + 1×）
=:
=7:17。
答：混合液中酒精和水的体积之比是7:17。
【变式9-2】一桶盐水200克，盐和水的质量比是1：24。要使盐水中，盐和水的质量比是1：29，要加入多少克水？
解：
200×÷-200
=8×30-200
=240-200
=40（克）。
答：要加入40克水。
点拨：原来盐占盐水的，现在盐占盐水的，盐水的浓度被加水稀释，这一过程中盐的重量不变；先根据原来的浓度求出盐的重量，再用盐的重量除以后来盐水的浓度，就是后来盐水的总重量，后来盐水的总重量减去原来盐水的总重量就是需要加水的重量。
【变式9-3】一种盐水中,盐与水的质量比是1：25，在520克这样的盐水中再加入5克盐,溶解后,盐水中盐与水的质量比是（ ）：（ ）。
解：
含盐：520×=20（克），
20+5=25（克），
含水：520×=500（克），
25：500=1：20。
答：溶解后,盐水中盐与水的质量比是1：20。
故答案为：1,20。
点拨：把这种盐水平均分成（1+25）份,其中盐占1份,水占25份,即盐占盐水的,这样可以求出在520克这样的盐水中含盐520×=20克,然后用20+5=25克,再求出在520克这样的盐水中含水520×=500克,那么盐与水的质量比是25：500,即1：20,据此解答即可。
【题型10 比的应用（分量÷对应分率=单位“1”）】
【例10】一批零件，已知加工完的个数与未加工的个数之比是1:3，再加工150个，已加工的零件个数与未加工的零件个数之比为2:3，则这批零件一共有多少个？
解：
150÷（ - ）
=150÷
=1000（个）.
答：这批零件一共有1000个。
点拨：与150个相对应的分率是（ - ），要求这批零件一共有多少个，根据数量÷对应的分率=单位“1”的量求解即可。
【变式10-1】光明小学原来体育达标人数与没有达标的人数比是3：5，后来又有60名同学达标，这时达标人数是没达标的，光明小学共有学生多少人？
解：
60÷（ - ）
=60÷（ - ）
=60÷
=60×
=800（人）。
答：光明小学共有学生800人。
点拨：由题意知道总人数不变，根据原来体育达标人数与没有达标的人数比是3：5，得出原来体育达标人数是总人数的，再由后来达标人数是没达标的，得出达标人数是总人数的，由此即可得出答案。
【变式10-2】皓午看一本小说，看了3天后他发现已经看的页数与还剩的页数比是4：5，如果再看25页就正好看了一半，这本书有多少页？
解：
25÷（ - ）
=25÷
=450（页）。
答：这本书有450页。
点拨：由“已经看的页数与剩下的页数的比是4：5”得出原来已看的页数占全书的，如果再看25页就正好看了一半，那么25页正好对应全书的（ - ），列式计算，解决问题。
【变式10-3】甲车间与乙车间的人数比是7：8，如果乙车间调16人到甲车间，两个车间的人数就一样多，甲、乙车间各有多少人？
解：
总人数：16÷（ - ）
=16÷
=480（人）；
甲车间人数：480×=224（人），
乙车间人数：480-224=256（人）。
答：原来甲车间人数是224人，乙车间人数是256人。
点拨：把两个车间的总人数看作单位“1”，则乙车间的人数占总数的 ；由“
如果乙车间调16人到甲车间，两个车间的人数就一样多”可知，此时乙车间的人数就占总人数的，则对应量16所对应的分率就是（ - ），用对应量除以对应分率就是两车间的总人数，进而可以求得每个车间的人数。
【题型11 比的应用（已知单位“1”用乘法）】
【例11】甲、乙、丙三个数的平均数是120，甲、乙、丙三个数的比是2：3：4，这三个数分别是多少？
解：
一份：
120×3÷（2+3+4）
=360÷9
=40，
甲：40×2=80，
乙：40×3=120，
丙：40×4=160。
答∶甲数是80，乙数是120，丙数是160。
点拨：题中已知三个数的平均数是120，所以应先求出这三个数的总和，再按2∶3∶4把三个数的总和进行分配，求出每个数具体是多少。
【变式11-1】煤场第一天运走600吨煤，正好占总储量的，第二天运走的与总储量的比是1：5，第二天运走多少吨？
解：
600÷×
=3600×
=720（吨）。
答：第二天运走720吨。
点拨：把煤场煤的总储量看作单位“1”，先根据分数除法意义，求出煤的总储量，第二天运走的与总储量的比是1：5，也就是说第二天运走的是总储量的，再依据分数乘法意义即可解答。
【变式11-2】学校运进480把扫把，要求把总数的放入仓库后，其余按4：5分给小学部和中学部，那么小学部和中学部各得多少把扫把？
解：
480×（1－）
=480×
=360（把），
360÷（4+5）×4=160（把），
360-160=200（把）。
答：小学部分160把扫把，中学部分200把扫把。
点拨：根据分数减法的意义求出分了几分之几；再根据分数乘法的意义，求出共分扫把的总数；又知道小学部和中学部按4:5分，分别求出小学部和中学部各占总数的几分之几；再根据求一个数的几分之几是多少用乘法，分别计算出小学部和中学部各分扫把的把数，据此解答。
【变式11-3】利民食品厂男职工、女职工的人数比是5:3，已知该食品厂共有职工184人，这个食品厂的男职工比女职工多多少人？
解：
184× + ）
=184×
=46（人）。
答：这个食品厂的男职工比妇职工多46人。
【题型12 比的应用（上坡、平路、下坡问题）】
【例12】一条公路全长60千米，分成上坡、平路、下坡三段，各段路程的长度之比是1：2：3，张叔叔骑车经过各段路所用时间之比是3：4：5，已知他在平路上骑车速度是每小时25千米。他行完全程用了多长时间？
解：
上坡路的长度：60×=10（千米），
平路的长度：60×=20（千米），
下坡路的长度：60﹣10﹣20=30（千米），
平路的时间：20÷25= （小时），
他行完全程用的时间： ÷4×（3+4+5）= （小时）。
答：他行完全程用小时。
点拨：根据各路段的长度之比，求出各段路占总长度的几分之几，然后根据分数乘法的意义分别求出三段路的长度；用平路的长度除以平路的速度求出平路的时间，再根据过各段路所用的时间比，求出平路的时间占总时间的几分之几，最后根据分数除法的意义求出行完全程的时间即可。
【变式12-1】一条路全长120km，上坡、平路、下坡三段路程之比是1:2:3，小明走完三段路程所用的时间之比是4:5:6，已知他上坡的速度是每小时5km，小明走完全程用了多长时间？
解：
上坡路：
120×=20（千米），
上坡时间：
20÷5=4（小时），
走完全程用时：
4÷4×（4+5+6）=15（小时）。
答：小明走完全程用了15小时。
【变式12-2】一条路全长60千米，分成上坡、平路、下坡三段，各段路程长的比依次是1：2：3，某人走各段路程所用时间比依次是4：5：6，已知他上坡的速度是每小时3千米，问此人走完全程用了多少时间？
解：
上坡用的时间为：
60×÷3
=60×÷3
=（小时），
根据所用时间比可知平路用时为：×=4（小时），
下坡路用时为：×=5（小时），
共用时间为：++5=12（小时）。
答：全程用了12小时。
点拨：本题可先根据全长和三段路程的比求出上坡路的长度，然后再根据上坡的速度求出上坡用的时间，就能根据他所用的时间比求出全程用了多长时间。
【变式12-3】一条河全长300km，分成上游、中游、下游三段，上游、中游、下游的距离之比是2∶5∶3，一条船行驶完这三段距离所用的时间之比是1∶3∶2，已知这条船在下游每小时行30km，这条船行驶完全程用了多长时间？
解：
下游路程：
300÷（2+5+3）×3
=300÷10×3
=30×3
=90（km），
下游行驶时间：
90÷30=3（小时），
全程行驶时间：
3÷2×（1+3+2）=9（小时）。
答∶这条船行驶完全程用了9小时的时间。
【题型13 按比分配（配套问题）】
【例13】装配自行车，3个工人2小时装配车架11个，4个工人3小时装配车轮20个。现有工人640个，为使车架、车轮装配成整车出厂，怎样安排这640个工人最合理？
解：
每个工人每小时装配车架：
11÷3÷2=（个），
每个工人每小时装配车轮：
20÷4÷3=（个）。
每个工人每小时装配的
车架：车轮 = ： =11：10，
工作量一定，工作效率与工作人数成反比，要使整车出厂，装配车架、车轮人数比：
：（×2）=5：11，
装配车架人数：
640÷（5+11）×5
=200（人），
装配车轮人数：
640-200=440（人）。
答：应安排200个工人装配车架，440个工人装配车轮。
点拨：根据工作总量÷工作时间÷工作人数=每人每小时的工作量分别求出装配车架和车轮的工作效率，并求出装配车架和车轮的速度比；因为一个车架要配两个车轮，所以可以找到装配车架与装配车轮的人数比；将640人按照装配车架和装配车轮的人数比进行分配，从而分别求出装配车架和装配车轮的人数。
【变式13-1】某车间有28名工人，生产某种螺栓和螺母，一个螺栓的两头各套上一个螺母配成一套，每人每天平均生产螺栓12个或螺母18个。问：多少名工人生产螺栓，多少名工人生产螺母，才能使一天所生产的螺栓和螺母刚好配套？
解法1：
每人每天生产螺栓或螺母的比：
12：18=2：3，
工作量一定，工作效率与工作人数成反比，要使螺栓、螺母刚好配套，生产螺栓、螺母人数比：
：（×2）=3：4，
生产螺栓人数：
28÷（3+4）×3
=12（人），
生产螺母人数：
28-12=16（人）。
答：12名工人生产螺栓，16名工人生产螺母，才能使一天所生产的螺栓和螺母刚好配套。
解法2：
设分配x人生产螺栓，则有（28-x）人生产螺母，根据题意，得12x×2=（28-x）×18，解得：x=12，
生产螺母的人数是：28-12=16
答：12名工人生产螺栓，16名工人生产螺母，才能使一天所生产的螺栓和螺母刚好配套。
【变式13-2】机械厂加工车间有85名工人，平均每人每天加工大齿轮16个或小齿轮10个，已知2个大齿轮与3个小齿轮配成一套，怎么安排生产，才能使每天加工的大小齿轮刚好配套？
解：
每人每天加工大齿轮或小齿轮的比：
16：10=8：5，
工作量一定，工作效率与工作人数成反比，要使大齿轮、小齿轮刚好配套，生产大齿轮、小齿轮人数比：
（2）：（×3）=12：5，
生产大齿轮人数：
85÷（12+5）×12
=60（人），
生产小齿轮人数：
85-60=25（人）。
答：安排60人生产大齿轮，25人生产小齿轮。
【变式13-3】某工艺品车间有20名工人，平均每人每天可制作12个大花瓶或10个小饰品，已知2个大花瓶与5个小饰品配成一套，则要安排多少名工人制作大花瓶，才能使每天制作的大花瓶和小饰品刚好配套？
解：
每人每天制作大花瓶或小饰品的比：
12：10=6：5，
工作量一定，工作效率与工作人数成反比，要想配套，制作大花瓶、小饰品人数比：
（2）：（×5）=1：3，
制作大花瓶人数：
20÷（1+3）×1
=5（人）。
答：安排5人制作大花瓶，才能使得每天制作的大花瓶和小饰品刚好配套。
【题型14 按比分配（分担费用问题）】
【例14】甲、乙、丙三人合租一辆车运送同样的货物从A地到B地，甲在全程的处卸货，乙在行程刚好一半的地方卸货，只有丙运到终点。共付运费440元，他们该怎样分摊运费比较合理？
解：
因运送同样的货物，按路程比分摊运费，比较合理。
甲、乙、丙分摊运费的比：
::1=2:3:6，
每份：440÷（2+3+6）=40（元），
甲：40×2=80（元），
乙：40×3=120（元），
丙：40×6=240（元）。
答：甲分摊运费80元，乙分摊运费120元，丙分摊运费240元，比较合理。
点拨：将全程看作单位“1”，则甲行，乙行，丙行1，其路程比就等于三人应分摊运费的比；根据上步结论求出三人应分摊的运费占总运费的分率，用它们分别乘总运费440元，即可解题。
【变式14-1】甲、乙、丙三人合作加工一批零件，加工一个零件甲需要6分钟，乙需要5分钟，丙需要4.5分钟，三人完成加工任务后共得工钱1590元。按照加工零件的数量分工钱，甲、乙、丙三人各得工钱多少元？
解：
甲、乙、丙工作量比：
：：=15：18：20，
一份：
1590÷（15+18+20）=30（元），
甲的工钱：30×15=450（元），
乙的工钱：30×18=540（元），
丙的工钱：30×20=600（元）。
答：甲、乙、丙三人各得工钱450元、540元、600元。
【变式14-2】甲、乙、丙三批货物总价值2580万元，甲、乙、丙三批货物的质量比为3:4:6，单价比为5:4:2，问：这三批货物各值多少万元？
解：
甲、乙、丙三批货物的价值比是：
（3×5）:（4×4）:（6×2）=15:16:12，
一份：
2580÷（15+16+12）=60（万元），
甲：
60×15=900（万元），
乙：
60×6=960（万元），
丙：
2580-900-960=720（万元）。
答：甲货物900万元，乙货物960万元，丙货物720万元。
点拨：甲、乙、丙三批货物的质量比为3:4:6，单价比为5:4:2，所以这三批货物的价值比是：（3×5）:（4×4）:（6×2）=15:16:12；再根据比与分数的关系，分别求出各种货物的价值占总价值的几分之几，然后结合三批货物的总价值为152万元，利用乘法运算，即可解答。
【变式14-3】
四位乘客合租一辆出租车，由于下车地点不同，每人承担的出租车费用各不相同。乘客甲付的车费与其他三位的比是1:2，乘客乙付的车费与其他三位的比是1:3，乘客丙付的车费与其他三位的比是1:4，乘客丁付车费26元。这四位乘客一共付出租车费多少钱？
解：
26÷（1- - - ）
=26÷（1 - ）
=26÷
=120（元）。
答：这四位乘客一共付的出租车费用是120元。
点拨：题目中出现了3个不同的单位“1”，解答问题时应注意找准单位“1”，求出26元所对应的分率是解决问题的关键。解答分数除法应用题时，要先明确单位“1”，再找出部分量所占的分率，根据部分量÷部分量的分率=单位“1”的量进行求解。
【题型15 按比分配（连比问题）】
【例15】甲、乙、丙三人合购一台空调，甲付钱数的等于乙付钱数的，等于丙付钱数的。已知丙比甲少付140元，这台空调多少元？
解：
令甲=乙=丙=1，
甲：乙：丙=3：4：=6：8：5，
140÷（6-5）×（6+8+5）=2660（元）。
答：这台空调2660元。
点拨：假设甲=乙=丙=1，求出甲：乙：丙，再根据甲乙丙付钱的比，和丙比甲少付140元，用除法求出这台空调的价钱，列式解答即可。
【变式15-1】一个水果店购进苹果的重量比橘子多25%，橘子与菠萝的重量的比是6:5，苹果比菠萝多160kg，该水果店购进苹果多少千克？
解：
苹果:橘子=（1+25%）:1=5:4，
苹果:橘子:菠萝=15:12:10，
苹果：
160÷（15-10）×15=480（kg）
答：水果店购进苹果480千克。
【变式15-2】有三箱水果共重60千克，如果从第一、二箱中都取出4千克水果放入第三箱中，则第一、二、三箱水果的质量比为1:2:3，问三箱水果原来分别重多少千克？
解：
后来，
一份质量：60÷（1+2+3）=10（千克），
第一箱：10×1=10（千克），
第二箱：10×2=20（千克），
第三箱：10×3=30（千克），
原来，
第一箱：10+4=14（千克），第二箱：20+4=24（千克），第三箱：30-4-4=22（千克）。
答：三箱水果原来分别重14千克、24千克、22千克。
【变式15-3】宽城区小学六年级三个班共收集废纸396kg。其中六（1）班收集的比六（2）班多，六（2）班与六（3）班收集废纸的比是10∶11。三个班各收集废纸多少千克？
解：
六（1）班∶六（2）班=6∶5=12∶10，
六（2）班∶六（3）班=10∶11，
六（1）班∶六（2）班∶六（3）班=12∶10∶11。
一份重：
396÷（12+10+11）=12（千克），
六（1）班：12×12=144（千克），
六（2）班：12×10=120（千克），
六（3）班：12×11=132（千克）。
答：六（1）班、六（2）班、六（3）班收集的废纸分别是144千克、120千克和132千克。
【题型16 按比分配（阴影部分面积问题）】
【例16】已知BC长10cm，直角三角形BCE的直角边EC长是8cm，阴影部分的面积比三角形EFG的面积大10cm2，求CF的长。
解：
如图，则（②+③）-①=10，
所以（②+③+④）-（①+④）=10，即平行四边形ABCD的面积比△BCE的面积大10平方厘米；
S△BCE=10×8÷2=40（平方厘米），
所以CF的长为：
（40+10）÷10
=50÷10
=5（cm）。
答：CF的长是5cm。
点拨：首先运用转化思想求出平行四边形ABCD与△BCE的面积之差；根据三角形的面积公式求出△BCE的面积，再运用平行四边形的面积公式求出CF的长。
【变式16-1】下图中平行四边形的面积是20平方厘米，阴影部分的面积是多少？
解：
20÷（2+3）×2÷2
=4×2÷2
=4（平方厘米）
答：阴影部分的面积是4平方厘米。
点拨：已知平行四边形的面积是20平方厘米，底是（2+3）厘米，根据面积公式求出它的高；由于三角形与平行四边形等高，且阴影部分（三角形）的底是2厘米，再根据三角形的面积公式列式计算即可。
【变式16-2】甲、乙两个圆的周长之比是2:3，若乙圆的面积是18平方厘米，则甲圆的面积是多少平方厘米？
解：
因为甲、乙两个圆的周长之比是2:3，
所以甲、乙两个圆的半径比是2:3，
则甲、乙两个圆的面积比是4:9，
则甲圆的面积为18×=8（平方厘米）。
答：甲圆的面积是8平方厘米。
点拨：分析题目，由甲、乙两个圆的半径比是2:3，可得甲、乙两个圆的面积比是4:9；然后根据乙圆的面积是18平方厘米，利用按比例分配进行解答即可。
【变式16-3】如图，大小两个正方形中涂色部分的面积比是3：2，则大小两个正方形的边长比是多少？面积比是多少？
解：
因为涂色部分两个三角形等高，
所以大小两个正方形的边长比是 3：2，面积比是32：22＝9：4，
答：大小正方形边长的比是3：2，面积的比是9：4。
点拨：涂色部分两个三角形等高，所以它们的面积比是3：2，就是大小两个正方形的边长比，那么面积比就是边长的平方比，据此解答即可。
【题型17 按比分配（求原比问题）】
【例17】甲、乙、丙三人共存款2980元，甲取出380元，乙存入700元，丙取出自己存款数的，这时三人存款数的比是5：3：2，现在三人的存款各是多少元？
解：
甲取出380元，乙存入700元，三人共存款：
2980-380+700=3300（元），
这时丙占总数的：2÷（1-）=3（份），
1份：
3300÷（5+3+3）
=3300÷11
=300（元）。
现在，
甲：300×5=1500（元），
乙：300×3=900（元），
丙，300×2=600（元）。
答：甲有1500元，乙有900元，丙有600元。
点拨：关键求出丙未取出自己存款数的时，甲、乙、丙三人存款数的比。
【变式17-1】甲、乙两根绳子共长22米，甲绳截去后，乙绳和甲绳的长度比是3：2，甲、乙两根绳子原来各长多少米？
解：
（1-）÷=，即乙甲原来的长度比是 6：5；
乙原来长：
22×
=22×
=12（米）；
甲原来长：
22×
=22×
=10（米）。
答：甲绳原长10米，乙绳原长12米。
点拨：已知甲、乙两根绳子共长22米，甲绳截去后还剩（1-）=，乙绳和甲绳的长度比是3：2，即甲的占是乙的，由此可得乙原来是甲的÷=，即乙甲原来的长度比是6：5，这样就能分别求甲乙原来长多少米．
【变式17-2】红绳子剪去后与绿绳子同样长，则红绳子长度与绿绳子长度的比是多少？
解：
红绳子长度与绿绳子长度的比是：
1：（1-）=1：=6：5。
答：红绳子与绿绳子的比是6:5。
点拨：把红绳子长度看作“1”，则绿绳子的长度是（1-），写出长度的比并化简成最简整数比即可。
【变式17-3】聪聪和笑笑共收集邮票171枚。已知聪聪邮票数的和笑笑邮票数的相等，求聪聪和笑笑各收集邮票多少枚。
解：
聪聪邮票数：笑笑邮票数=：=4：5，
聪聪：
171÷（4+5）×4=76（枚），
笑笑：
171-76=95（张）。
答：聪聪收集76张邮票，笑笑收集95张邮票。