2023-2024学年甘肃省定西市临洮县九年级上学期12月月考数学模拟试题（含答案）

这是一份2023-2024学年甘肃省定西市临洮县九年级上学期12月月考数学模拟试题（含答案），共11页。试卷主要包含了选择题，填空题，计算题等内容，欢迎下载使用。

本试卷满分为120分，考试时间为100分钟．
一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项，将此选项的字母填在答题卡上．
1．一道选择题共有4个答案，其中有且只有一个是正确的，有一位同学随意地选了一个答案，那么他选对的概率为（ ）
A．1 B． C． D．
2．一元二次方程x(x－2)＝x－2的解是（ ）
A．x1＝1，x2＝2 B．x1＝x2＝1 C．x1＝0，x2＝2 D．x1＝x2＝0
3．已知x＝1是一元二次方程(m－2)x2+4x－m2＝0的一个根，则m的值为（ ）
A．－1或2 B．－1 C．2 D．0
4．抛物线y＝(x－2)2+3的顶点是（ ）
A．(2，－3) B．(1，4) C．(2，3) D．(3，4)
5．若A(－4，y1)，B(－3，y2)，C(1，y3)为二次函数y=x2+4x－5的图象上的三点，则y1，y2，y3的大小关系是（ ）
A．y3＜y1＜y2 B．y2＜y1＜y3 C．y1＜y2＜y3 D．y1＜y3＜y2
6．已知⊙O的半径为1，点P到圆心O的距离为d，若关于x的方程x2－2x＋d=0有实根，则点P（ ）
A．在⊙O的内部 B．在⊙O的外部 C．在⊙O上 D．在⊙O上或⊙O的内部
7．等边三角形的内切圆半径、外接圆半径和高的比是（ ）
A．1∶∶ B．1∶2∶ C．1∶2∶3 D．1∶∶2
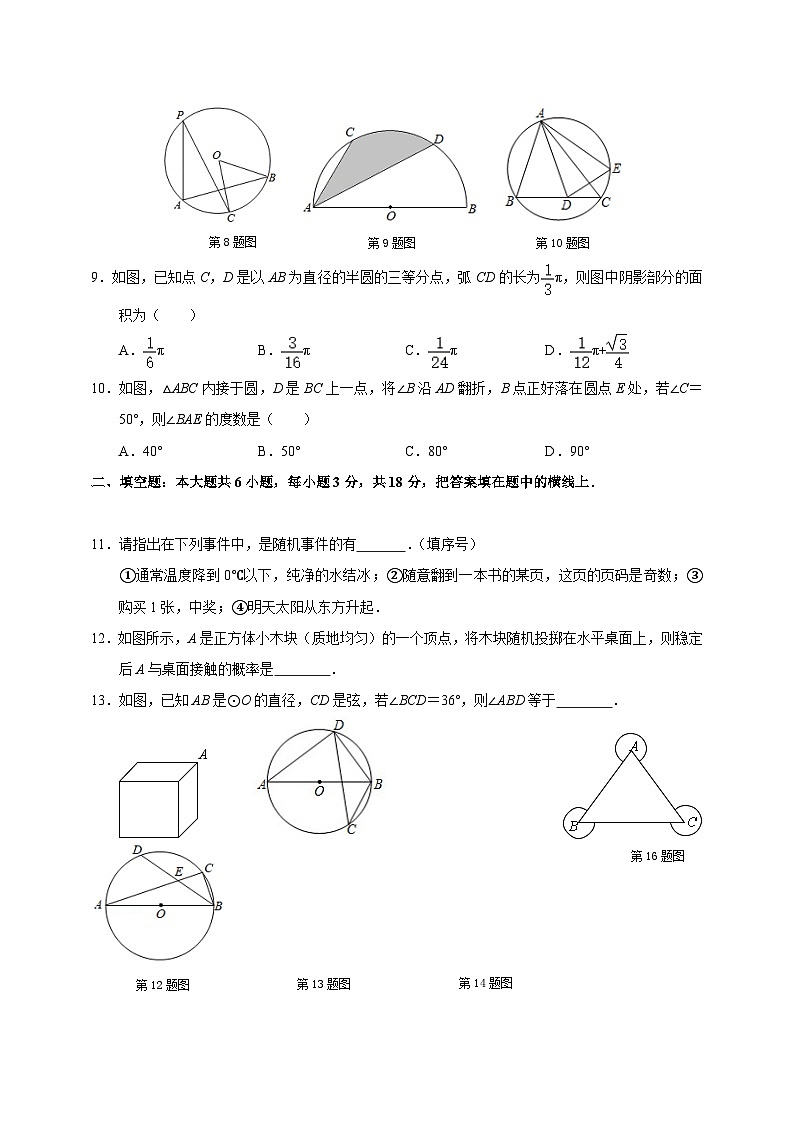
8．如图，⊙O中，OC⊥AB，∠APC＝28°，则∠BOC的度数为（ ）
A．14° B．28° C．42° D．56°
第8题图

第10题图
第9题图
9．如图，已知点C，D是以AB为直径的半圆的三等分点，弧CD的长为π，则图中阴影部分的面积为（ ）
A．π B．π C．π D．π+
10．如图，△ABC内接于圆，D是BC上一点，将∠B沿AD翻折，B点正好落在圆点E处，若∠C＝50°，则∠BAE的度数是（ ）
A．40° B．50° C．80° D．90°
二、填空题：本大题共6小题，每小题3分，共18分，把答案填在题中的横线上．

11．请指出在下列事件中，是随机事件的有 ．（填序号）
①通常温度降到0℃以下，纯净的水结冰；②随意翻到一本书的某页，这页的页码是奇数；③购买1张，中奖；④明天太阳从东方升起．
如图所示，A是正方体小木块（质地均匀）的一个顶点，将木块随机投掷在水平桌面上，则稳定后A与桌面接触的概率是 ．
13．如图，已知AB是⊙O的直径，CD是弦，若∠BCD＝36°，则∠ABD等于 ．
第16题图
A


第13题图
第12题图
第14题图
14．如图，的边长都大于2，分别以它的顶点为圆心，1为半径画弧（弧的端点分别在三角形的相邻两边上），则这三条弧的长的和是 ．
15．圆锥的底面圆的周长是4πcm，母线长是6cm，则该圆锥的侧面展开图的圆心角的度数 ．
16．如图，在半径为3的⊙O中，AB是直径，AC是弦，D是弧AC的中点，AC与BD交于点E． 若E是BD的中点，则AC的长是 ．
三、计算题：本大题共11小题，共72分，解答时，必须写出必要的解题步骤．
17．（8分）选择最佳方法解下列一元二次方程．
（1）x2－6x＋8＝0； （2）2x2－4x＋3＝0．
18．（5分）已知二次函数的图象经过点(0，－3)，且顶点坐标为(1，－4)．求这个解析式．
19．（6分）关于x的一元二次方程x2－3x－k＝0有两个不相等的实数根．
（1）求k的取值范围；
（2）请选择一个k的负整数值，并求出方程的根．
20．（6分）把二次函数配方成y＝a(x－h)2＋k的形式，并写出它的图象的开口方向、顶点坐标、对称轴．
21．（5分）有一人患了流感，经过两轮传染后，共有121人患了流感，求每轮传染中平均每人传染了多少个人．
22．（6分）已知：抛物线y＝x2－3x－4与x轴交于点A、B（点A在点B的左侧），与y轴交于点C．求△ABC的面积．
23．（5分）已知：如图，⊙O是Rt△ABC的内切圆，∠C=90°，AC=12cm，BC=9cm，求⊙O的半径r．
24．（5分）往半径为26cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽AB＝48cm，求水的最大深度．
25．（6分）如图，AB是半圆AOB的直径，C是半圆上的一点，AD平分∠BAC交半圆于点D，过点D作DH⊥AC与AC的延长线交于点H．
求证：DH是半圆的切线．
（8分）如图，⊙O是△ABC的外接圆，其切线AE与直径BD的延长线相交于点E，且
AE=AB．
（1）求∠ACB的度数；
（2）若DE=2，求⊙O的半径．

（12分）如图，在平面直角坐标系中，抛物线y＝ax2＋bx－2交x轴于A，B两点，交y轴
于点C，且OA＝2OC＝8OB，点P是第三象限内抛物线上的一动点．
（1）求此抛物线的表达式；
（2）若PC∥AB，求点P的坐标；
（3）连接AC，求△PAC面积的最大值及此时点P的坐标．
数学答案
一、选择题（每小题3分，共30分）
1．D 2．A 3．B 4． C 5．B 6．D 7．C 8．D 9．A 10．C
二、填空题（每小题3分，共18分）
11．②③ 12．13．54° 14．5π15．120°
三、计算题
17．（8分）（1）x1＝2，x2＝4；（4分）（2）没有实数根（4分）．
18．（5分）解：设解析式为y＝a(x－h)2＋k ………………（1分）
∵h=1 k=－4
∴y＝a(x－1)2－4 ………………（2分）
把（0，－3）代入，得
－3＝a(x－1)2－4
a=1………………（1分）
解析式为：y＝(x－1)2－4．
或＝x2－2x－3． ………………（1分）19．（6分）解：（1）∵方程有两个不相等的实数根，
∴ ＞0．
即 ，解得：． ………………（3分）
（2）若k是负整数，k只能为－1或－2． ………………（1分）
如果k＝－1，原方程为 ．
解得，． ………………（2分）
（如果k＝－2，原方程为，解得，，．）
20．（6分）； ………………（3分）
开口：向上；顶点坐标为：；对称轴为：直线x＝3． ………………（3分）
21．（5分）解：设每轮传染中平均每人传染了x人．
依题意，得1+x+x（1+x）＝121，
即（1+x）2＝121，………………（3分）
解方程，得x1＝10，x2＝﹣12（舍去）．………………（2分）
答：每轮传染中平均每人传染了10人．
22．（6分）解：令y=0，则x2－3x－4=0
解得 x1＝－1，x2＝4
∴A（－1，0），B（4，0） ………………（2分）
令x=0，则y=－4
∴C（0，－4） ………………（2分）
∴．………………（2分）
23.（5分）解：证明：连接OD，OE，OF．
在Rt△ACB中，
………………（2分）
∵四边形CDOF是正方形，
∴CD=CF=r.
∵⊙O是Rt△ABC的内切圆
∴AD=AE=12-r，BE=BF=9-r，………………（2分）
∵AE+BE=5，
∴（12-r）+（9-r）=15
即r=3．………………（1分）
或．………………（3分）
24．（5分）解：连接OB，过点O作OC⊥AB于点D，交⊙O于点C，如图所示：
∵AB＝48，
∴BD＝AB＝×48＝24，………………（2分）
∵⊙O的直径为52，
∴OB＝OC＝26，
在Rt△OBD中，OD＝＝＝10，………………（2分）
∴CD＝OC﹣OD＝26﹣10＝16（cm）．………………（1分）
25．（6分）证明：连接OD，
∵OA＝OD，
∴∠DAO＝∠ADO，
∵AD平分∠BAC，
∴∠CAD＝∠OAD，
∴∠CAD＝∠ADO，
∴AH∥OD，
∵DH⊥AC，
∴OD⊥DH，
∴DH是半圆的切线．………………（6分）
26．（8分）（1）如图，连接.
∵是的切线，
∴.
又∵，
∴.
∵，
∴，
∴.
又∵在中，，
∴.∴.
∴.
∴.………………（5分）
（2）设的半径为，
在中，∵，∴.
∴.∴.
∴.
∴的半径是2．.………………（3分）
（12分）解：（1）由可得点，即．
∵，∴，． ………………（1分）
把，两点坐标代入，解得，，
∴抛物线的表达式为．………………（3分）
（2）∵，，∴点的纵坐标为－2，
∴．
解得，（舍）．
∴ ………………（3分）
（3）设直线的表达式为（），
把代入可得，
∴直线的表达式为. ………………（2分）
过点作轴的垂线，垂足为，交线段于点；
过点作，为垂足．
设点（），则点， ………………（1分）
∴．
∴
∴当时，．
，
故点． ………………（2分）
题号
一
二
三
总分
得分
得分
评卷人