新教材适用2024版高考数学二轮总复习第1篇专题6概率与统计第3讲统计与成对数据的分析核心考点4独立性检验教师用书

这是一份新教材适用2024版高考数学二轮总复习第1篇专题6概率与统计第3讲统计与成对数据的分析核心考点4独立性检验教师用书，共3页。
K2＝eq \f(nad－bc2,a＋ba＋cb＋dc＋d)(其中n＝a＋b＋c＋d为样本容量)．
典例研析· 悟方法
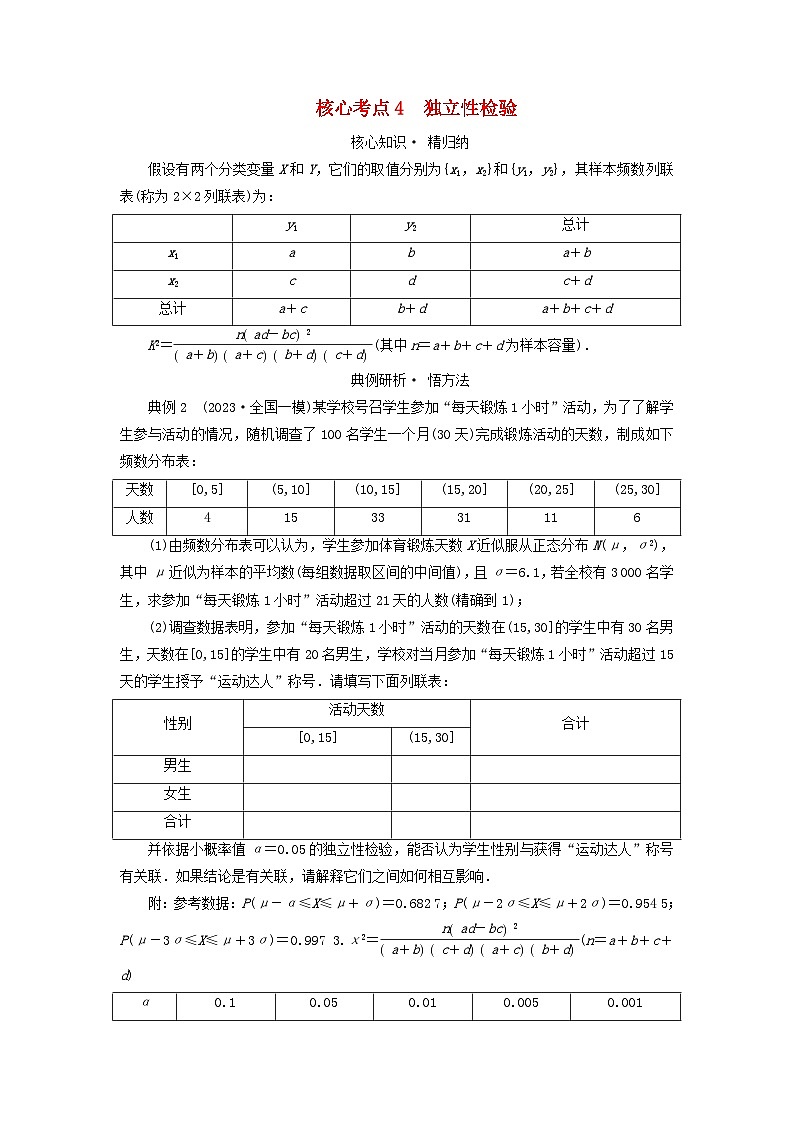
典例2 (2023·全国一模)某学校号召学生参加“每天锻炼1小时”活动，为了了解学生参与活动的情况，随机调查了100名学生一个月(30天)完成锻炼活动的天数，制成如下频数分布表：
(1)由频数分布表可以认为，学生参加体育锻炼天数X近似服从正态分布N(μ，σ2)，其中μ近似为样本的平均数(每组数据取区间的中间值)，且σ＝6.1，若全校有3 000名学生，求参加“每天锻炼1小时”活动超过21天的人数(精确到1)；
(2)调查数据表明，参加“每天锻炼1小时”活动的天数在(15,30]的学生中有30名男生，天数在[0,15]的学生中有20名男生，学校对当月参加“每天锻炼1小时”活动超过15天的学生授予“运动达人”称号．请填写下面列联表：
并依据小概率值α＝0.05的独立性检验，能否认为学生性别与获得“运动达人”称号有关联．如果结论是有关联，请解释它们之间如何相互影响．
附：参考数据：P(μ－α≤X≤μ＋σ)＝0.682 7；P(μ－2σ≤X≤μ＋2σ)＝0.954 5；P(μ－3σ≤X≤μ＋3σ)＝0.997 3.χ2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)(n＝a＋b＋c＋d)
【解析】 (1)由频数分布表知μ＝eq \f(4×2.5＋15×7.5＋33×12.5＋31×17.5＋11×22.5＋6×27.5,100)＝14.9，
则X～N(14.9,6.12)，∵P(μ－σ≤X≤μ＋σ)＝0.682 7，
∴P(X＞21)＝P(X＞14.9＋6.1)＝eq \f(1－0.682 7,2)＝0.158 65，
∴3 000×0.158 65＝475.95≈476，
∴参加“每天锻炼1小时”活动超过21天的人数约为476人．
(2)由频数分布表知，锻炼活动的天数在[0,15]的人数为：4＋15＋33＝52，∵参加“每天锻炼1小时”活动的天数在[0,15]的学生中有20名男生，∴参加“每天锻炼1小时”活动的天数在[0,15]的学生中有女生人数：52－20＝32，
由频数分布表知，锻炼活动的天数在(15,30]的人数为31＋11＋6＝48，∵参加“每天锻炼1小时”活动的天数在(15,30]的学生中有30名男生，∴参加“每天锻炼1小时”活动的天数在(15,30]的学生中有女生人数：48－30＝18，
列联表如下：
零假设为H0：学生性别与获得“运动达人”称号无关，χ2＝eq \f(100×30×32－20×182,50×50×52×48)≈5.769＞3.841，
依据α＝0.05的独立性检验，我们推断H0不成立，即：可以认为学生性别与获得“运动达人”称号有关；
而且此推断犯错误的概率不大于0.05，根据列联表中的数据得到，男生、女生中活动天数超过15天的频率分别为：eq \f(30,50)＝0.6和eq \f(18,50)＝0.36，可见男生中获得“运动达人”称号的频率是女生中获得“运动达人”的称号频率的eq \f(0.6,0.36)≈1.67倍，于是依据频率稳定与概率的原理，我们可以认为男生获得“运动达人”的概率大于女生，即男生更容易获得运动达人称号．
方法技巧· 精提炼
独立性检验的一般步骤
(1)根据样本数据制成2×2列联表．
(2)根据公式χ2＝eq \f(nad－bc2,a＋ba＋cb＋dc＋d)计算．
(3)比较χ2与临界值的大小关系，作统计推断．
加固训练· 促提高
(2023·日照模拟)第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术，是实现人、机、物互联的网络基础设施．某市工信部门为了解本市5G手机用户对5G网络的满意情况，随机抽取了本市200名5G手机用户进行调查，所得情况统计如下：
(1)完成上述列联表，并估计本市5G手机用户对5G网络满意的概率；
(2)依据小概率值α＝0.05的独立性检验，分析本市5G手机用户对5G网络满意与年龄在50岁以下是否有关．
附：
χ2＝eq \f(nad－bc2,a＋bc＋da＋cb＋d)，其中n＝a＋b＋c＋d.
【解析】 (1)2×2列联表如下：
所以本市5G手机用户对5G网络满意的概率约为eq \f(150,200)＝eq \f(3,4).
(2)零假设为H0：本市5G手机用户对5G网络满意与年龄在50岁以下无关．
根据列联表中的数据，计算可得
χ2＝eq \f(200×95×25－25×552,120×80×150×50)＝eq \f(25,9)≈2.778