人教版2023-2024学年九年级上册期末模拟数学练习卷（含解析）

这是一份人教版2023-2024学年九年级上册期末模拟数学练习卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.3左右，则布袋中白球可能有( )
A．15个B．20个C．30个D．35个
2．在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
A．12B．13C．23D．14
3．方程x2=2x的解是（ ）
A．x=0B．x=2C．x1=0，x2=2D．x1=0，x2= 2
4．用配方法解方程 x2−2x−5=0 时，原方程应变形为（ ）
A．(x+1)2=6B．(x+2)2=9C．(x−1)2=6D．(x−2)2=9
5．将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为（ ）
A．y=（x﹣1）2+4B．y=（x﹣4）2+4
C．y=（x+2）2+6D．y=（x﹣4）2+6
6．如图，抛物线 y=x2−2x−3 与 y 轴交于点 A ，与 x 轴的负半轴交于点 B ，点 M 是对称轴上的一个动点.连接 AM，BM ，当 |AM−BM| 最大时，点 M 的坐标是（ ）
A．(1，4)B．(1，2)C．(1，−2)D．(1，−6)
7．如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝25°．将△ABC绕点C顺时针旋转α角（0°＜α＜180°）至△A'B'C使得点A′恰好落在AB边上，则α等于（ ）
A．55°B．50°C．65°D．60°
8．如图，在△ABC中，∠BAC=90°，AB=6，AC=8．将△ABC绕点A旋转至△ADE，使AD⊥BC，DE交边AC于点F，则AF的长是（ ）
A．4B．245C．5D．6
9．如图，△ABC 内接于⊙O， CD 是⊙O的直径，∠ BCD =54° .则∠ A 的度数是 （ ）
A．36°B．33°C．30°D．27°
10．如图，AC，BC是两个半圆的直径，∠ACP=30°，AB=10 cm，则PQ的长为（ ）．
A．5cmB．53cmC．6cmD．8cm
二、填空题
11．点 P(−1，2) 关于原点的对称点的坐标为 ．
12．一元二次方程x2−3=0的解为 ．
13．关于x的一元二次方程ax2+2x+1＝0有两个不相等的实数根，则实数a的取值范围是 ．
14．如图，一抛物线型拱桥，当拱顶到水面的距离为2米时，水面宽度为4米；那么当水位下降1.5米后，水面的宽度为 米．
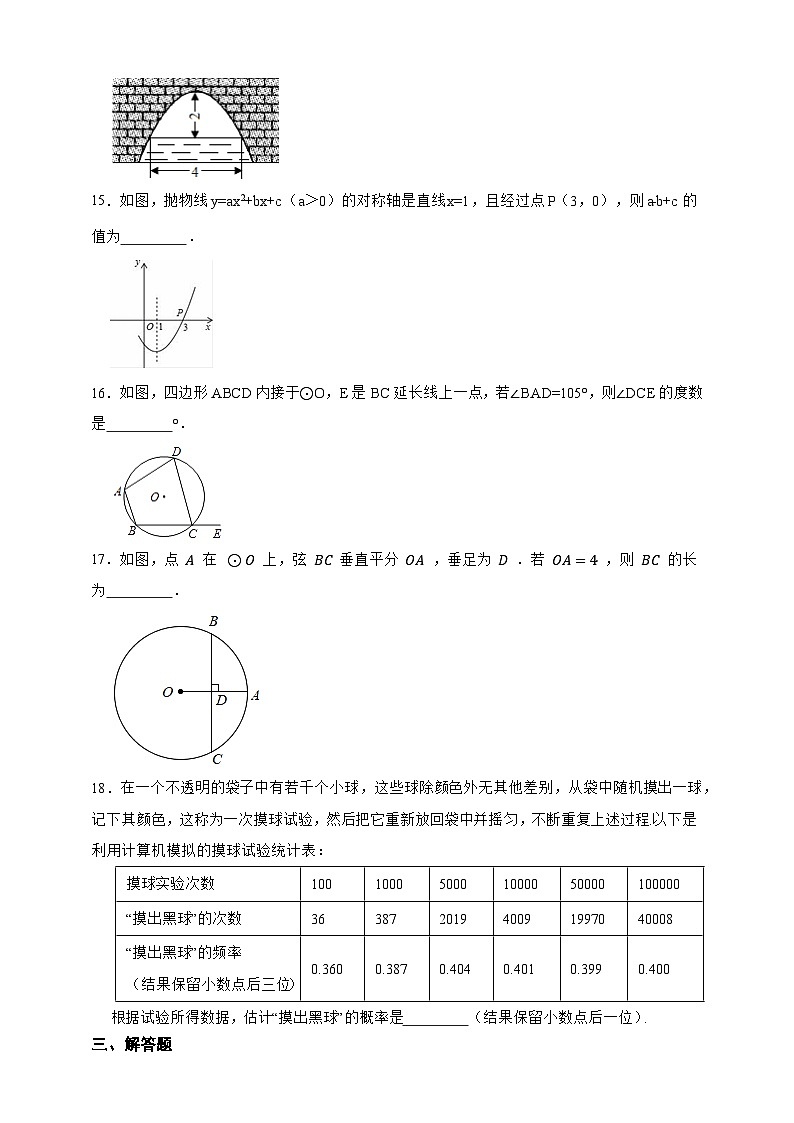
15．如图，抛物线y=ax2+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a﹣b+c的值为 ．
16．如图，四边形ABCD内接于⊙O，E是BC延长线上一点，若∠BAD=105°，则∠DCE的度数是 °．
17．如图，点 A 在 ⊙O 上，弦 BC 垂直平分 OA ，垂足为 D ．若 OA=4 ，则 BC 的长为 ．
18．在一个不透明的袋子中有若千个小球，这些球除颜色外无其他差别，从袋中随机摸出一球，记下其颜色，这称为一次摸球试验，然后把它重新放回袋中并摇匀，不断重复上述过程.以下是利用计算机模拟的摸球试验统计表：
根据试验所得数据，估计“摸出黑球”的概率是 （结果保留小数点后一位）.
三、解答题
19．已知x1、x2是一元二次方程x2−3x−2=0的两个根，求2x1x2−x1−x2的值.
20．一个不透明的袋中装有2个白球，1个红球.这些球除颜色外，没有任何其他区别，有如下两个活动：
活动1：从袋中随机摸出一个球，记下颜色，然后从袋中剩余的球中再随机摸出一个球，摸出的两个球都是白球的概率记为P1；
活动2：从袋中随机摸出一个球，记下颜色，然后把这个球放回袋中并摇匀，重新从袋中随机摸出一个球，两次摸出的球都是白球的概率记为P2.
试猜想P1，P2的大小关系，并用画树状图或列表的方法列出所有可能的结果，验证你的猜想.
21．已知关于x的一元二次方程mx2−(m+2)x+m4=0两个不相等的实数根x1，x2，若1x1+1x2=4m，求m的值．
22．如图所示，二次函数y=(x−1)(x−a)(a为常数)的图象的对称轴为直线x=2.
（1）求a的值.
（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式.
23．如图，⊙O的直径AB和弦CD相交于点E．已知AE=1，EB=5，∠DEB=60°，求CD 的长．
24．如图所示，在△ABC中，∠BAC=90°，点E在BC边上，且CA=CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF.
（1）求证：四边形DCFG是平行四边形.
（2）当BE=4，CD=38AB时，求⊙O的直径长.
25．已知直线y=2x+4与x轴、y轴分别交于A，D两点，抛物线y=−12x2+bx+c经过点A，D，B是抛物线与x轴的另一个交点.
（1）求这条抛物线的函数表达式及点B的坐标.
（2）设M是直线AD上一点，且S△AOM：S△OMD=1：3，求点M的坐标.
（3）如果C(2，y)在这条抛物线上，在y轴的正半轴上是否存在点P，使△BCP为等腰三角形?若存在，请求出点P的坐标；若不存在，请说明理由.
答案解析部分
1．【答案】D
【解析】【解答】设袋中有黄球x个，由题意得 ，
解得x=15，则白球可能有50-15=35个．
故选D．
【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近即此时频率=概率，可以从比例关系入手，设未知数列出方程求解．
2．【答案】B
【解析】【解答】解：随机闭合开关S1、S2、S3中的两个，即：S1+S2 ， S1+S3 ， S2+S3
∴共3种情况
根据题意，得能让灯泡L1发光的组合为： S1+S2
∴能让灯泡L1发光的概率是 13.
故答案为：B.
【分析】列举出所有可能出现的情况数，然后找出能让灯泡L1发光的组合数，接下来利用概率公式进行计算.
3．【答案】C
【解析】【解答】解：x2﹣2x=0
x（x﹣2）=0
∴x1=0，x2=2．
故选C．
【分析】把右边的项移到左边，用提公因式法因式分解，可以求出方程的两个根．
4．【答案】C
【解析】【解答】由原方程移项，得
x²−2x=5，
方程的两边同时加上一次项系数−2的一半的平方1，得
x²−2x+1=6
∴(x−1) ²=6.
故答案为：C.
【分析】根据完全平方公式为a2±2ab+b2=a±b2求解即可。
5．【答案】B
【解析】【解答】解：将y=x2﹣2x+3化为顶点式，得y=（x﹣1）2+2．
将抛物线y=x2﹣2x+3向上平移2个单位长度，再向右平移3个单位长度后，得到的抛物线的解析式为y=（x﹣4）2+4，
故选：B．
【分析】根据函数图象向上平移加，向右平移减，可得函数解析式．
6．【答案】D
【解析】【解答】解：根据三角形三边的关系得：
|AM−BM| ≤AB，当ABM三点共线时取等号，
当 B，A，M三点共线时， |AM−BM| 最大，
则直线 AB 与对称轴的交点即为点 M .
由 y=x2−2x−3 可知， A(0，−3)，B(−1，0) ，
对称轴 x=−b2a=−−22=−1
设直线 AB 为 y=kx+b .
∴b=−3−k+b=0
∴k=−3b=−3
故直线 AB 解析式为 y=−3x−3
当 x=1 时， y=−3×1−3=−6
∴M(1，−6) .
故答案为：D.
【分析】先根据题意求出点A、点B的坐标，抛物线的对称轴为x=1，根据三角形三边的关系得 |AM−BM| ≤AB，当A、B、M三点共线时取等号，即M点是x=-1与直线AB的交点时， |AM−BM| 最大.求出点M的坐标即可.
7．【答案】B
【解析】【解答】∵∠ACB=90 ° ，∠ABC=25°，
∴∠A=90 ° ﹣∠B=65 ° ，
由旋转的性质得：CA=CA′，
∴∠A=∠CA′A=65 ° ，
∴α=∠ACA′=180 ° ﹣2×65°=50 ° ，
故答案为：B．
【分析】在Rt△ABC中，∠ACB=90 ° ，∠ABC=25°，得出∠A的度数，又由将△ABC绕点C顺时针旋转α角（0°＜α＜180°）至△A'B'C，易得△ACA′是等边三角形，继而求得答案。
8．【答案】C
【解析】【解答】解： ∵在△ABC中，∠BAC=90°，AB=6，AC=8 ，
∴BC=AB2+AC2=62+82=10，
∵ 将△ABC绕点A旋转至△ADE，
∴∠DAE=∠BAC=90°，DE=BC=10，∠E=∠C，即AD⊥AE，
又 AD⊥BC，
∴AE∥BC，
∴∠EAC=∠C，
∴∠EAF=∠E，
∴AF=EF，
∵∠E+∠D=90°，∠EAF+∠DAF=90°，
∴∠D=∠DAF，
∴AF=DF，即F是DE的中点，
∴AF=12DE=5.
故答案为：C.
【分析】在△ABC中，用勾股定理算BC的长，由旋转得∠DAE=∠BAC=90°，DE=BC=10，∠E=∠C，推出AE∥BC，结合平行线的性质推出∠EAF=∠E，由同角的余角相等得∠D=∠DAF，由等边对等角得AF=EF=DF，即F是DE的中点，最后根据直角三角形斜边上的中线等于斜边的一半即可得出答案.
9．【答案】A
【解析】【解答】连接BD，
∵CD是⊙O的直径，
∴∠CBD＝90°，
∵∠BCD＝54°，
∴∠D＝90°−∠BCD＝36°，
∴∠A＝∠D＝36°．
故答案为：A．
【分析】首先连接BD，由CD是⊙O的直径，根据直径所对的圆周角是直角，即可求得∠CBD的度数，继而求得∠D的度数，然后由圆周角定理，求得∠A的度数．
10．【答案】B
【解析】【解答】 解：如图，连接AP，BQ．
∵AC，BC是两个半圆的直径，点P在半圆上，
∴∠APC=90°，∠BQC=90°．
∵∠ACP=30°，
∴CP =AC·cs∠ACP= 32AC，CQ= BC·cs∠ACP= 32BC.
∴PQ = CP - CQ = 32（AC - BC）= 32AB= 32×10 = 53cm.
故答案为：B.
【分析】根据半圆所对圆周角是直角，判断∠APC=90°，∠BQC=90°．然后根据30°角的三角函数值表示CP，CQ，最后根据线段的和差求解即可.
11．【答案】（1，−2）
【解析】【解答】点P（－1，2）关于原点的对称点的坐标为（1，－2），
故答案为（1，－2）．
【分析】根据关于原点的对称点的坐标特征，变化符号写出坐标即可。
12．【答案】x1=3，x2=−3
【解析】【解答】解：∵x2−3=0
∴x2=3，
∴x1=3，x2=−3，
故答案为：x1=3，x2=−3．
【分析】利用直接开平方法解方程即可。
13．【答案】a＜1且a≠0
【解析】【解答】∵关于x的一元二次方程ax2+2x+1＝0有两个不相等的实数根，
∴△＝b2﹣4ac＝22﹣4×a×1＝4﹣4a＞0，
解得：a＜1，
∵方程ax2+2x+1＝0是一元二次方程，
∴a≠0，
∴a的范围是：a＜1且a≠0．
故答案为：a＜1且a≠0．
【分析】由关于x的一元二次方程ax2+2x+1=0有两个不相等的实数根，即可得判别式△＞0，继而可求得a的范围．
14．【答案】27
【解析】【解答】解：如图：以拱顶到水面的距离为2米时的水面为x轴，拱顶所在直线为y轴建立平面直角坐标系，
根据题意设二次函数解析式为：y=ax2+2，
把A（2，0）代入，得
a=-12，
所以二次函数解析式为：y=-12x2+2，
当y=-1.5时，-12x2+2=-1.5，
解得x=±7．
所以水面的宽度为27．
故答案为：27．
【分析】利用待定系数法求出二次函数解析式为：y=-12x2+2，再求出-12x2+2=-1.5，最后求解即可。
15．【答案】0
【解析】【解答】由题意可知，抛物线的对称轴为x=1，且经过点P（3，0），
∴抛物线与x轴的另一个交点是（-1，0），
代入抛物线解析式y=ax2+bx+c中，得a-b+c=0．
故答案为：0．
【分析】已知“对称轴是直线x=1，且经过点P（3，0）”，根据抛物线的对称性可知抛物线与x轴的另一个交点是（-1，0），代入抛物线即可求解．
16．【答案】105
【解析】【解答】∵四边形ABCD是圆内接四边形，∴∠DAB+∠DCB=180°，∵∠BAD=105°，∴∠DCB=180°﹣∠DAB=180°﹣105°=75°，∵∠DCB+∠DCE=180°，∴∠DCE=∠DAB=105°．
【分析】利用圆内接四边形对角互补，外角等于其内对角，可求出∠DCE=∠DAB=105°．
17．【答案】43
【解析】【解答】解：连接OC，
∵弦 BC 垂直平分 OA ，
∴∠COD=90°，BD=CD，OD=AD，
∴OD= 12 OA= 12 ×4=2，
∴CD= OC2−OD2=42−22=23 ，
∴BC=2CD= 43 ，
故答案为： 43 ．
【分析】连接OC，根据垂径定理和垂直平分线的性质得到BD=CD，OD=AD，再利用勾股定理求出CD，即可得到BC的长。
18．【答案】0.4
【解析】【解答】解：观察表格发现随着摸球次数的增多频率逐渐稳定在0.4附近，
故摸到白球的频率估计值为0.4；
故答案为0.4.
【分析】利用频率估计概率进行解答即可.
19．【答案】解：∵是一元二次方程x2−3x−2=0的两个根，
∴x1+x2=3，x1x2=−2，
∴2x1x2−x1−x2=2x1x2−(x1+x2)=2×(−2)−3=−7.
【解析】【分析】根据根与系数的关系可得x1+x2=3，x1x2=-2，将待求式变形为2x1x2-(x1+x2)，然后代入进行计算.
20．【答案】解：活动1：
∵共有6种等可能的结果，摸到两个白球的有2种情况，
∴摸出的两个球都是白球的概率记为P1=26=13
活动2：
∵共有9种等可能的结果，摸到两个白球的有4种情况，
∴摸出的两个球都是白球的概率记为P2=49
∴P1【解析】【分析】根据活动1、活动2列出表格，找出所有可能的情况数以及摸到两个白球的情况数，根据概率公式求出相应的概率，然后进行比较即可.
21．【答案】解：∵x1，x2是一元二次方程mx2−(m+2)x+m4=0的两根
∴由根与系数关系得x1+x2=−−(m+2)m=m+2m，x1x2=14，
∵1x1+1x2=4m，
∴x1+x2x1x2=4m，
∴4(m+2)m=4m，即m2−m−2=0，
解得m1=2，m2=−1，
∵Δ=b2−4ac=(m+2)2−4m⋅m4>0，
∴m>−1
∴m=2．
【解析】【分析】先求出 x1+x2=−−(m+2)m=m+2m，x1x2=14， 再利用一元二次方程根的判别式求解即可。
22．【答案】（1）解：y=（x-1）（x-a）=x2-（1+a）x+a，
∵抛物线的对称轴为直线x=2，
∴−−1+a2=2
解之：a=3.
（2）解：y=x2-4x+3=（x-2）2-1，
∵ 向下平移该二次函数的图象，使其经过原点，
设平移后的函数解析式为y=（x-2）2-1-k，
∴4-1-k=0
解之：k=3，
∴y=（x-2）2-1-3=x2-4x.
【解析】【分析】（1）将函数解析式转化为一般形式，利用抛物线的对称轴，可求出a的值.
（2）将函数解析式转化为顶点式，利用二次函数图象平移规律，设平移后的函数解析式为y=（x-2）2-1-k，将（0，0）代入函数解析式，可求出k的值，即可得到平移后的函数解析式.
23．【答案】解：作OF⊥CD于点F ，连结OD，
AB=AE+ BE =6，即⊙O的半径为3．
在Rt△OEF中，OE=OA-AE=3-1=2，∠DEB=60° ，则∠EOF=30° ，OF= 3，
在Rt△ODF中，DF= OD2−OF2=9−3=6，
∴CD=2DF= 26．
【解析】【分析】作OF⊥CD于点F ， 连结OD， 先求出 ⊙O 的半径，再根据勾股定理求出OF和DF的长，最后利用垂径定理求出CD的长.
24．【答案】（1）证明：如图所示，连结AE.
∵∠BAC=90°，∴CF是⊙O的直径.∵AC=EC，∴CF⊥AE，∵AD为⊙O的直径，∴∠AED=90°，即GD⊥AE，∴CF//DG，∵AD为⊙O的直径，∴∠ACD=90°，∴∠ACD+∠BAC=180°，∴AB//CD，∴四边形DCFG为平行四边形.
（2）由CD=38AB，可设CD=3x，AB=8x，∴CD=FG=3x.
∵∠AOF=∠COD，∴AF=CD=3x，∴BG=8x−3x−3x=2x.
∵GE//CF，∴BEEC=BGGF=23.
又∵BE=4，∴AC=CE=6，即BC=6+4=10，∴AB=102−62=8x，解得x=1.
在Rt△ACF中，AF=3，AC=6，∴CF=32+62=35，即⊙O的直径长为35
【解析】【分析】（1）连接AE，利用圆周角定理可证得CF是圆O的直径及∠AED=90°，利用垂径定理可证得CF⊥AE，同时可证得DG⊥AE，可推出CF∥DG，利用圆周角定理可证得∠ACD=90°，利用平行线的判定定理可证得AB∥CD，利用有两组对边分别平行的四边形是平行四边形，可证得结论.
（2）利用已知设CD=3x，BA=8x，可表示出CD，FG的长；再表示出AF，BG的长；利用平行线分线段成比例定理可求出CE的长，同时可求出BC的长，利用勾股定理求出x的值，可得到AF，然后利用勾股定理求出CF的长，即可得到圆的直径长.
25．【答案】（1）解：∵ 直线y=2x+4与x轴、y轴分别交于A，D两点，
∴当x=0时y=4
当y=0时2x+4=0，
解之：x=-2，
∴点A（-2，0），点D（0，4），
∴c=4−12×4−2b+c=0
解之：b=1c=4
∴抛物线的函数表达式为y=−12x2+x+4，
当y=0时，−12x2+x+4=0
解之：x1=4，x2=-2，
∴B（4，0）
（2）解：当点M在线段AD上时，过点M作MN⊥x轴于点N，
∵S△AOM：S△OMD=1：3，
∴AM：MD=1：3，
∴AM：AD=1：4，
∵MN∥y轴，
∴△AMN∽△AOD，
∴MNOD=AMAD=14即MN4=14，
解之：MN=1，
当y=1时2x+4=1，
解之：x=−32
∴M(−32，1)
当点M′在线段DA的延长线上时，过点M′作M′N′⊥x轴于点N′
∴M′N′∥y轴，
∴△AM′N′∽△AOD，
∴M′N′DO=AM′AD=12即M'N'4=12，
解之：M′N′=2，
当y=-2时，2x+4=-2，
解之：x=-3；
∴点M′（-3，-2）
综上所述，点M的坐标为M(−32，1)或（-3，-2）
（3）解：当x=2时y=−12×4+2+4=4，
∴点C（2，4），
设点P（0，m）（m＞0），
∵点B（4，0），
∴CP2=4+（4-m）2=m2-8m+20，BP2=16+m2，BC2=4+16=20，
当PB=BC时，则16+m2=20
解之：m1=2，m2=-2（舍去），
∴点P（0，2）；
当PB=CP时，则m2-8m+20=16+m2，
解之：m=12，
∴点P（0，12）；
当CP=BC时m2-8m+20=20，
解之：m1=0（舍去），m2=8（舍去）
.综上所述，在y轴的正半轴上存在点P（0，12）或（0，2）使△BCP为等腰三角形.
【解析】【分析】（1）利用直线y=2x+4的解析式，由x=0求出对应的y的值，由y=0求出对应的x的值，可得到点A，D的坐标，将点A，D代入抛物线函数解析式，可求出b，c的值，可得到抛物线的函数解析式；再由y=0，可得到关于x的方程，解方程求出x的值，可得到点B的坐标.
（2）分情况讨论：当点M在线段AD上时，过点M作MN⊥x轴于点N，利用两三角形的面积之比，可求出AM：AD=1：4，由MN∥y轴，可证得△AMN∽△AOD，利用相似三角形的性质可求出MN的长，将y=1代入一次函数解析式，可求出对应的x的值，可得到点M的坐标；当点M′在线段DA的延长线上时，过点M′作M′N′⊥x轴于点N′，可证得△AM′N′∽△AOD，利用相似三角形的性质可求出M′N′的长，将y=-2代入函数解析式，可求出对应的x的值，可得到点M的坐标，综上所述可得到符合题意的点M的坐标.
（3）将x=2代入抛物线的解析式，可求出点C的坐标，设点P（0，m）（m＞0），由点B的坐标，利用两点之间的距离公式，分别表示出CP2，BP2，BC2，利用等腰三角形的性质，分情况讨论：当PB=BC时；当PB=CP时；当CP=BC时；分别可得到关于m的方程，分别解方程求出m的值，可得到符合题意的点P的坐标.
摸球实验次数
100
1000
5000
10000
50000
100000
“摸出黑球”的次数
36
387
2019
4009
19970
40008
“摸出黑球”的频率
（结果保留小数点后三位）
0.360
0.387
0.404
0.401
0.399
0.400
白球1
白球2
红球
白球1

（白1，白2）
（白1，红）
白球2
（白2，白1）

（白2，红）
红球
（红，白1）
（红，白2）

白球1
白球2
红球
白球1
（白1，白1）
（白1，白2）
（白1，红）
白球2
（白2，白1）
（白2，白2）
（白2，红）
红球
（红，白1）
（红，白2）
（红，红）