
浙教版3.1 圆课时训练
展开1.在Rt△ABC中,AB=6,BC=8,将此三角形覆盖最小圆的半径为 .
2.抛物线与两轴交于三点,覆盖这三个点的最小圆的半径为 .
3.已知中,,,,将此三角形覆盖最小圆的半径为 .
4.如图,三个全等的边长为16的正方形品字摆放,则覆盖三个正方形最小的圆的半径为 .
连心线取到最近与最远
例1.已知⊙O的半径为5cm,点P到⊙O的最近距离是2,那么点P到⊙O的最远距离是 .
例2.已知点,⊙C的半径为1 ,是⊙C内或上的一个动点,则的最小值为 .
练习1:如图,菱形ABCD的边长为13,对角线交于点O,OB=12.约定:三角形三边上的任意一点到圆上任意一点距离的最小值叫做三角形与圆的距离,若三角形与⊙C的距离为3,则⊙C的半径为 .
练习2:如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最大值是 .
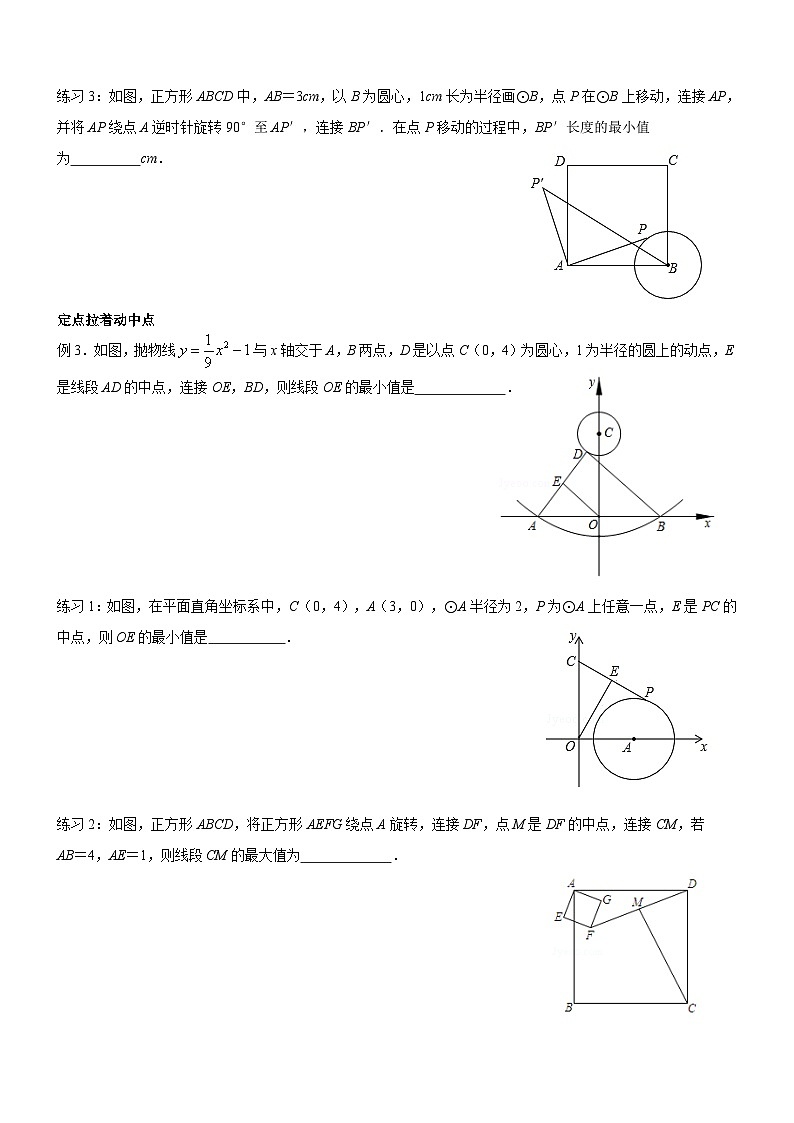
练习3:如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值
为 cm.
定点拉着动中点
例3.如图,抛物线与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是 .
练习1:如图,在平面直角坐标系中,C(0,4),A(3,0),⊙A半径为2,P为⊙A上任意一点,E是PC的中点,则OE的最小值是 .
练习2:如图,正方形ABCD,将正方形AEFG绕点A旋转,连接DF,点M是DF的中点,连接CM,若
AB=4,AE=1,则线段CM的最大值为 .
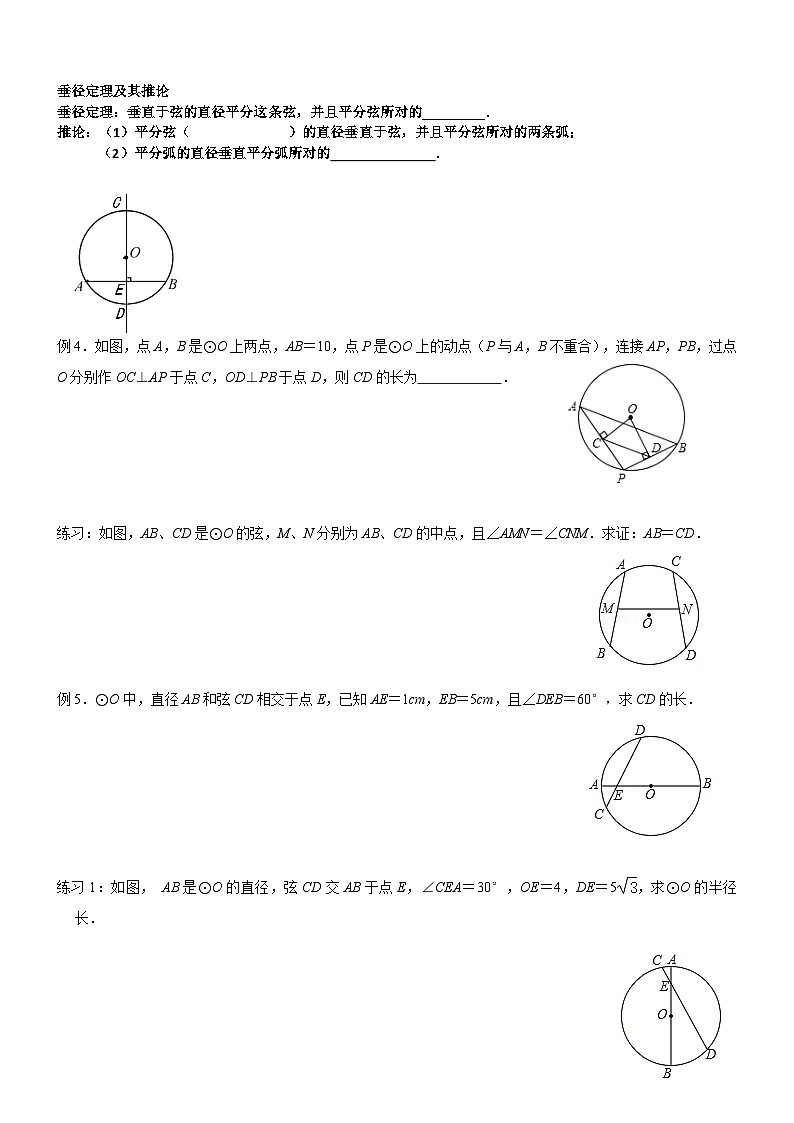
垂径定理及其推论
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的_________.
推论:(1)平分弦( )的直径垂直于弦,并且平分弦所对的两条弧;
(2)平分弧的直径垂直平分弧所对的 .
例4.如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP,PB,过点O分别作OC⊥AP于点C,OD⊥PB于点D,则CD的长为 .
练习:如图,AB、CD是⊙O的弦,M、N分别为AB、CD的中点,且∠AMN=∠CNM.求证:AB=CD.
例5.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
练习1:如图, AB是⊙O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求⊙O的半径长.
练习2:如图,P为⊙O内的一个定点,A为⊙O上的一个动点,射线AP、AO分别与⊙O交于B、C两点.若⊙O的半径长为3,OP=,则弦BC的最大值为 .
例6.某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=48cm,则圆柱形饮水桶的底面半径的最大值是 cm.
练习1:等腰△ABC的三个顶点都在⊙O上,底边BC=8cm,⊙O半径为5cm,求S△ABC.
练习2:如图,半径为2的圆的圆心在坐标原点,两条互相垂直的弦AC和BD相交于点M(1,),求四边形ABCD面积的最大值和最小值.
《圆》提升1测试 姓名( )
1.一个点到圆的最大距离为11cm,最小距离为5cm,则圆的半径为 .
2.已知一个直角三角形的面积为12cm2,周长为cm,覆盖这个直角三角形的最小圆的半径是 cm.
3.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上,那么覆盖△ABC的最小圆半径是 .
4.如图,在平面直角坐标系中,点A(3,4),B(3,0),以A为圆心,2为半径作⊙A,点P为⊙A上一动点,M为OP的中点,连接BM,设BM的最大值为m,最小值为n,则的值为 .
5.如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,则CE= .
(第3题) (第4题) (第5题)
6.如图,在△ABC中,AC=BC=5,AB=6,点D为AC上一点,作DE∥AB交BC于点E,点C关于DE的对称点为点O,以OA为半径作⊙O恰好经过点C,并交直线DE于点M,N.则MN的值为 .
(第6题) (第7题) (第8题)
7.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为 .
8.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,平面上有一点P,连接AP,CP,且CP=2,取AP的中点M.连接BM,则BM的最小值为 .
9.如图,直线AB经过⊙O的圆心,与⊙O相交于点A、B,点C在⊙O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与⊙O相交于点Q,点P在直线AB的适当位置上时,QP=QO.这样的点P共有 个,并相应地求出∠OCP的度数.
10.如图,在半径为2的⊙O中有一点E,过点E的弦AB与CD互相垂直,且OE=1,
(1)求AB2+CD2的值;
(2)求证:AE2+CE2+EB2+ED2为定值;
(3)求证:AC2+BC2+BD2+AD2为定值.
《圆》提升1作业 姓名( )
1.下列每张方格纸上都有一个三角形,只用圆规就能作出三角形的外接圆的是( )
A.①② B.①③ C.②④ D.③④
2.如图,以AB为直径的半圆O上有两点D、E,ED与BA的延长线交于点C,且有DC=OE,若∠C=20°,则∠EOB的度数是( )
A.40°B.50°C.60°D.80°
3.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为 .
4.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为 .
5.如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO=BE,则线段BE= .
(第2题) (第3题) (第4题) (第5题)
6.如图,AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,则弦CD= .
7.在△ABC中,AB=AC=2,∠BAC=120°,则能完全覆盖住此三角形的最小圆的面积为 .
8.如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点F,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CFP与△DFQ的面积和为 .
9.小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为cm2,则该圆的半径为 cm.
(第6题) (第8题) (第9题)
10.如图,在半径为的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,求CD的长.
11.如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=,点E在弧AD上,射线AE与CD的延长线交于点F.若AE=6,求EF的长.
12.已知两同心圆的圆心为O,过小圆上一点M作小圆的弦MA和大圆的弦BMC,且MA⊥BC,
求证:AB2+BC2+CA2为定值.
数学九年级上册3.1 圆优秀课后练习题: 这是一份数学九年级上册3.1 圆优秀课后练习题,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学九年级上册3.1 圆同步练习题: 这是一份数学九年级上册3.1 圆同步练习题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
浙教版九年级上册3.1 圆课后练习题: 这是一份浙教版九年级上册3.1 圆课后练习题,文件包含31圆2022年浙教版初中数学七年级上册同步练习解析版doc、31圆2022年浙教版初中数学七年级上册同步练习试卷版doc等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。













