初中数学浙教版九年级上册3.6 圆内接四边形当堂检测题

这是一份初中数学浙教版九年级上册3.6 圆内接四边形当堂检测题，共10页。试卷主要包含了如图,点A、B、C、D、E都是等内容，欢迎下载使用。
知识点 圆内接四边形及其性质
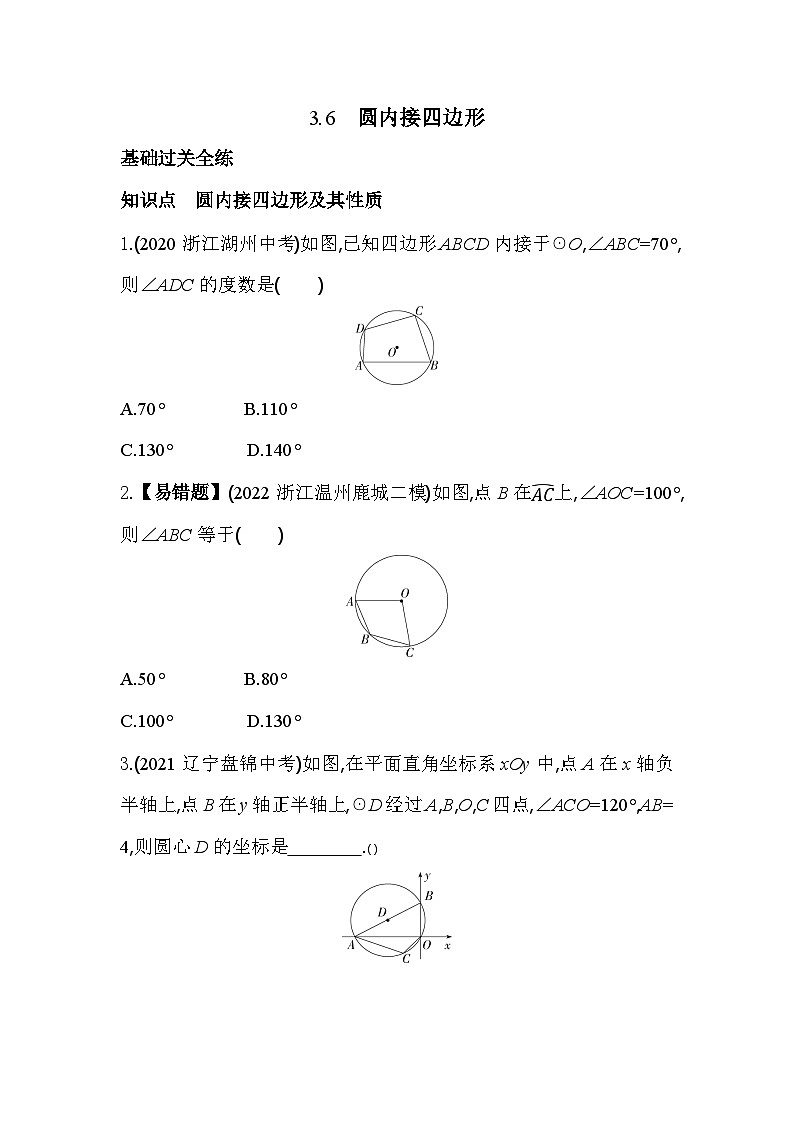
1.(2020浙江湖州中考)如图,已知四边形ABCD内接于☉O,∠ABC=70°,则∠ADC的度数是( )
A.70° B.110°
C.130° D.140°
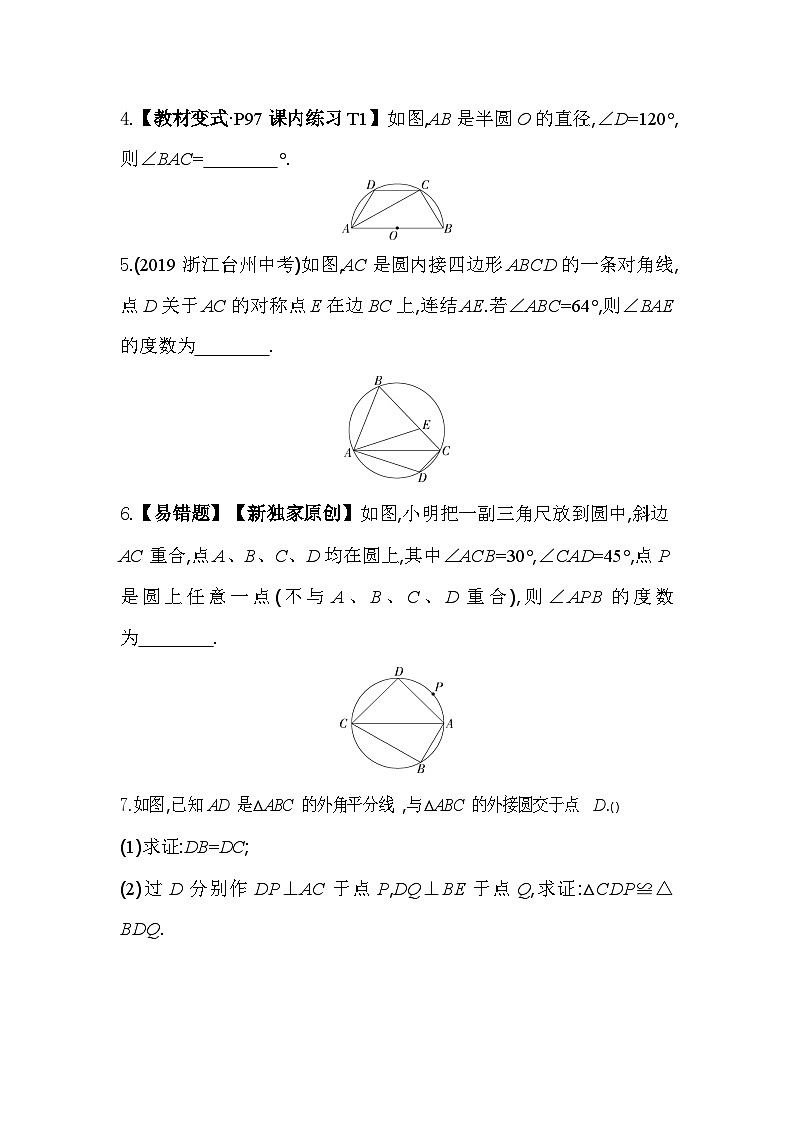
2.【易错题】(2022浙江温州鹿城二模)如图,点B在AC上,∠AOC=100°,则∠ABC等于( )
A.50° B.80°
C.100° D.130°
3.(2021辽宁盘锦中考)如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,☉D经过A,B,O,C四点,∠ACO=120°,AB=
4,则圆心D的坐标是 .( )
4.【教材变式·P97课内练习T1】如图,AB是半圆O的直径,∠D=120°,则∠BAC= °.
5.(2019浙江台州中考)如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连结AE.若∠ABC=64°,则∠BAE的度数为 .
6.【易错题】【新独家原创】如图,小明把一副三角尺放到圆中,斜边AC重合,点A、B、C、D均在圆上,其中∠ACB=30°,∠CAD=45°,点P是圆上任意一点(不与A、B、C、D重合),则∠APB的度数为 .
7.如图,已知AD是△ABC的外角平分线,与△ABC的外接圆交于点D.( )
(1)求证:DB=DC;
(2)过D分别作DP⊥AC于点P,DQ⊥BE于点Q,求证:△CDP≌△BDQ.
能力提升全练
8.【一题多解】(2023浙江温州龙港期中,6,★☆☆)已知在圆的内接四边形ABCD中,∠A∶∠B∶∠C=2∶3∶7,则∠D的度数为( )
A.40° B.60°
C.100° D.120°
9.(2023浙江杭州萧山期中,7,★★☆)如图,点A、B、C、D、E都是
☉O上的点,AC=AE,∠D=130°,则∠B的度数为( )
A.130° B.128°
C.115° D.116°
10.【数学文化】(2020湖南株洲中考,18,★★☆)斛是中国古代的一种量器.据《汉书·律历志》记载:“斛底,方而圜(huán)其外,旁有庣(tiā)焉.”意思是说:“斛的底面为正方形的四个顶点都在一个圆上,此圆外有一个同心圆.”如图所示,问题:现有一斛,其底面的外圆直径为五尺(即5尺),“庣旁”为五寸(即两同心圆的外圆与内圆的半径之差为0.5尺),则此斛底面的正方形的边长为 尺.
11.【等面积法】(2023浙江杭州西湖期中,19,★★☆)如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)试判断△ABC的形状,并给出证明;
(2)若AB=2,AD=1,求CD、BD的长度.
素养探究全练
12.【推理能力】如图1,在☉O中,弦AD平分圆周角∠BAC,我们将圆中以A为公共点的三条弦BA,CA,DA构成的图形称为圆中“爪形A”.如图2,四边形ABCD内接于圆O,AB=BC,
(1)证明:圆中存在“爪形D”;
(2)若∠ADC=120°,求证:AD+CD=BD.

答案全解全析
基础过关全练
1.B ∵四边形ABCD内接于☉O,∠ABC=70°,
∴∠ADC=180°-∠ABC=180°-70°=110°.
2.D 如图,在优弧AC(不与点A、C重合)上取点D,连结AD、CD,
由圆周角定理得∠ADC=12∠AOC=50°,
∵四边形ABCD为圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC=180°-50°=130°,故选D.
3.答案 (-3,1)
解析 ∵四边形ABOC为圆内接四边形,
∴∠ABO+∠ACO=180°,∵∠ACO=120°,
∴∠ABO=180°-120°=60°.
∵∠AOB=90°,∴AB为☉D的直径,
∴D为AB的中点,
在Rt△ABO中,∵∠ABO=60°,∴∠OAB=30°,
∴OB=12AB=2,∴OA=23,
∴A(-23,0),B(0,2),
∴点D的坐标为(-3,1).
4.答案 30
解析 ∵四边形ABCD为圆内接四边形,
∴∠B+∠D=180°,
∵∠D=120°,∴∠B=60°,
∵AB是半圆O的直径,∴∠ACB=90°,
∴∠BAC+∠B=90°,
∴∠BAC=30°.
5.答案 52°
解析 由已知得,∠D=180°-∠ABC=116°,
∵点D关于AC的对称点E在边BC上,∴∠D=∠AEC=116°,
∴∠BAE=∠AEC-∠ABC=116°-64°=52°.
6.答案 30°或150°
解析 当点P在优弧BCA上时,∠APB=∠ACB=30°;
当点P在劣弧AB上时,四边形ACBP为圆内接四边形,
∴∠APB+∠ACB=180°,∴∠APB=180°-30°=150°.
∴∠APB的度数为30°或150°.
7.证明 (1)∵AD是△ABC的外角平分线,
∴∠EAD=∠DAC,
∵四边形ABCD为圆内接四边形,
∴∠BAD+∠DCB=180°,∵∠EAD+∠BAD=180°,
∴∠EAD=∠DCB,
∵∠DAC=∠DBC,∴∠DCB=∠DBC,∴DB=DC.
(2)∵AD平分∠EAC,DP⊥AC,DQ⊥BE,
∴DQ=DP,
在Rt△CDP与Rt△BDQ中,DC=DB,PD=QD,
∴Rt△CDP≌Rt△BDQ(HL).
能力提升全练
8.D 解法一:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°,
∵∠A∶∠B∶∠C=2∶3∶7,
∴∠A∶∠B∶∠C∶∠D=2∶3∶7∶6,
∴∠D=180°×63+6=120°,故选D.
解法二:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°,
∵∠A∶∠B∶∠C=2∶3∶7,
设∠A=2x,∠B=3x,∠C=7x,
∴2x+7x=180°,解得x=20°.
∴∠B=60°,
∴∠D=180°-∠B=120°,故选D.
9.C 如图,连结AC、CE,
∵点A、C、D、E都是☉O上的点,
∴∠CAE+∠D=180°,
∵∠D=130°,
∴∠CAE=180°-130°=50°,
∵AC=AE,
∴∠ACE=∠AEC=12×(180°-50°)=65°,
∵点A、B、C、E都是☉O上的点,
∴∠AEC+∠B=180°,
∴∠B=180°-65°=115°,
故选C.
10.答案 22
解析 如图,∵四边形CDEF为正方形,
∴∠D=90°,CD=DE,∴CE为直径,∠ECD=45°,
由题意得AB=5尺,∴CE=5-0.5×2=4尺,
∵CD2+DE2=CE2,CD=DE,
∴2CD2=16,∴CD=22尺.
11.解析 (1)△ABC是等腰直角三角形.
证明:∵AC为☉O的直径,
∴∠ADC=∠ABC=90°,
∵∠ADB=∠CDB,
∴AB=BC,
∴AB=BC,
又∵∠ABC=90°,
∴△ABC是等腰直角三角形.
(2)在Rt△ABC中,AB=BC=2,
∴AC=2,
在Rt△ADC中,AD=1,AC=2,
∴CD=AC2-AD2=3,
过A作AE⊥BD于E,过C作CF⊥BD于F,如图,
则△ADE和△CDF均是等腰直角三角形,
∴AE=22AD=22,CF=22CD=62,
∵S四边形ABCD=S△ACD+S△ABC=S△ABD+S△BCD,
∴12×1×3+12×2×2=12×22BD+12×62BD,
∴BD=2+62.
素养探究全练
12.证明 (1)∵AB=BC,
∴AB=BC,
∴∠ADB=∠CDB,
∴DB平分圆周角∠ADC,
∴圆中存在“爪形D”.
(2)如图,延长DC至点E,使得CE=AD,连结BE,
∵∠A+∠DCB=180°,∠ECB+∠DCB=180°,
∴∠A=∠ECB,
∵CE=AD,AB=BC,
∴△BAD≌△BCE(SAS),
∴∠E=∠ADB,BD=BE,
由(1)知,DB平分圆周角∠ADC,∠ADC=120°,
∴∠ADB=12∠ADC=60°,
∴∠E=∠ADB=60°,
∴△BDE是等边三角形,
∴DE=BD,∴AD+CD=BD.