中考数学二轮培优复习《几何模型》专题19 瓜豆原理中动点轨迹圆或圆弧型最值问题（2份打包，原卷版+教师版）

这是一份中考数学二轮培优复习《几何模型》专题19 瓜豆原理中动点轨迹圆或圆弧型最值问题（2份打包，原卷版+教师版），文件包含中考数学二轮培优复习《几何模型》专题19瓜豆原理中动点轨迹圆或圆弧型最值问题教师版doc、中考数学二轮培优复习《几何模型》专题19瓜豆原理中动点轨迹圆或圆弧型最值问题学生版doc等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。

【知识精讲】
如图，P是圆O上一个动点，A为定点，连接AP，Q为AP中点．
考虑：当点P在圆O上运动时，Q点轨迹是？
【分析】观察动图可知点Q轨迹是个圆，而我们还需确定的是此圆与圆O有什么关系？
考虑到Q点始终为AP中点，连接AO，取AO中点M，则M点即为Q点轨迹圆圆心，半径MQ是OP一半，任意时刻，均有△AMQ∽△AOP，QM:PO=AQ:AP=1:2．
【小结】确定Q点轨迹圆即确定其圆心与半径，
由A、Q、P始终共线可得：A、M、O三点共线，由Q为AP中点可得：AM=1/2AO．
Q点轨迹相当于是P点轨迹成比例缩放．
根据动点之间的相对位置关系【分析】圆心的相对位置关系；
根据动点之间的数量关系【分析】轨迹圆半径数量关系．
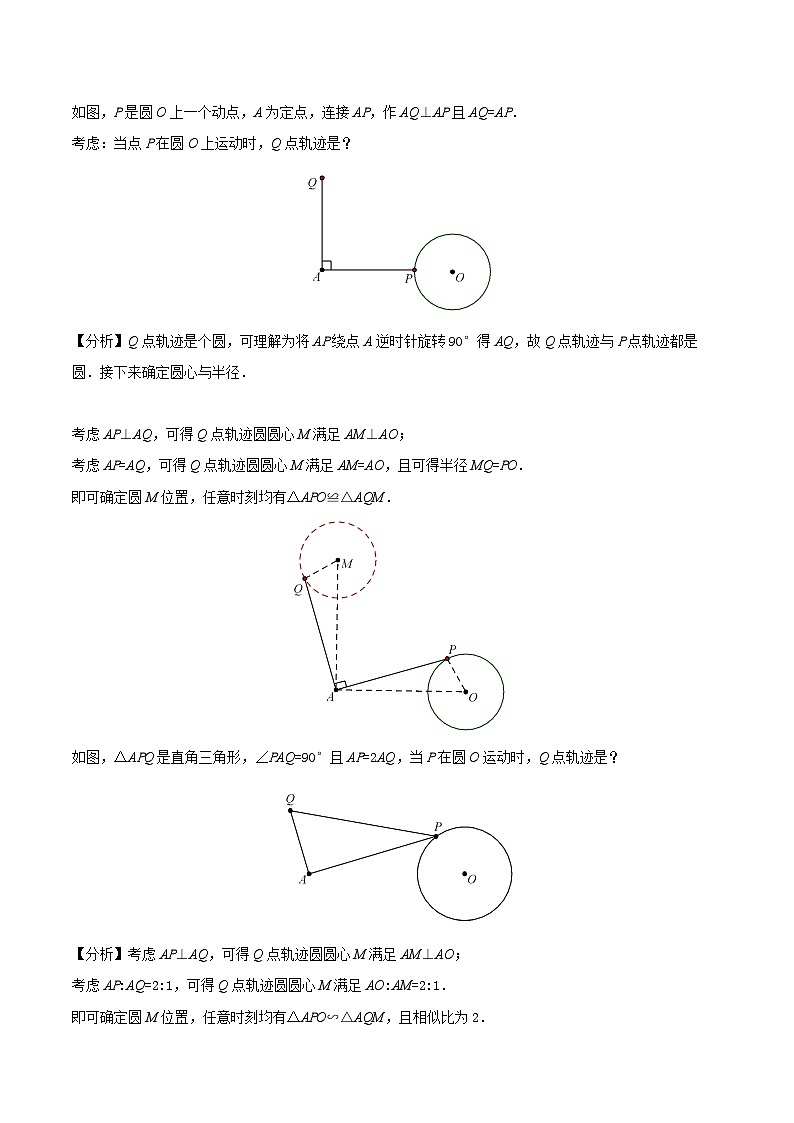
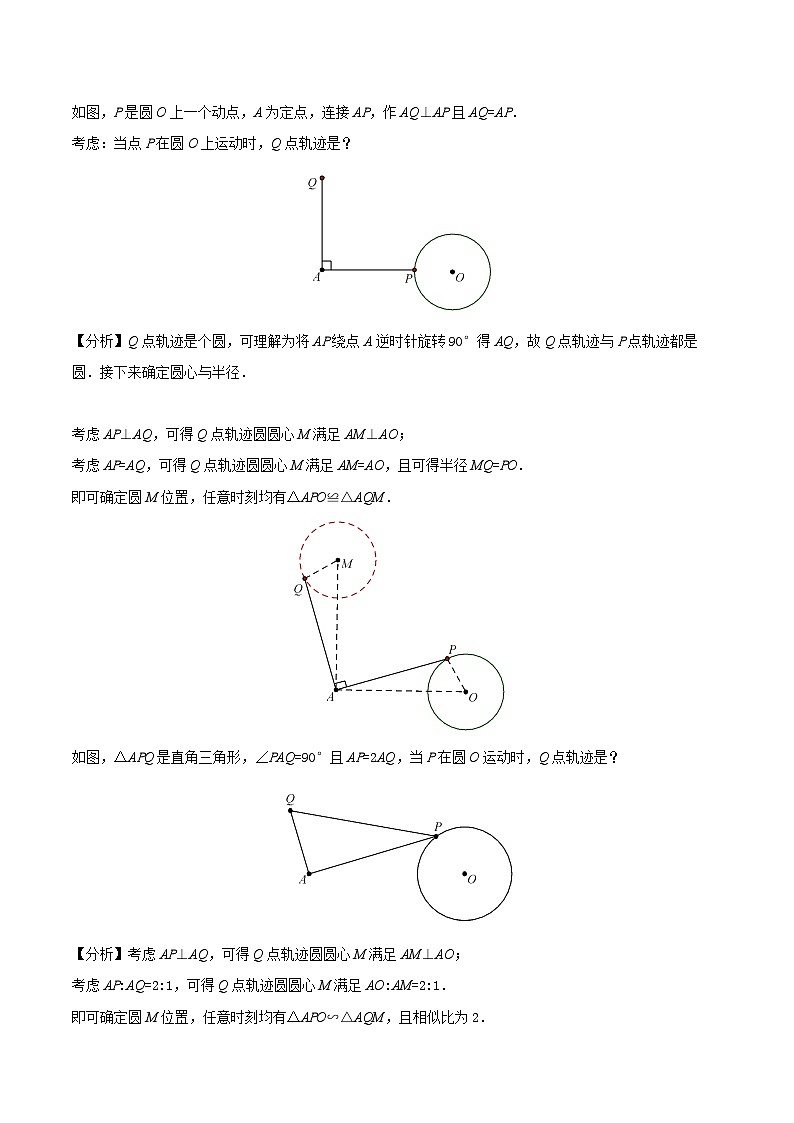
如图，P是圆O上一个动点，A为定点，连接AP，作AQ⊥AP且AQ=AP．
考虑：当点P在圆O上运动时，Q点轨迹是？
【分析】Q点轨迹是个圆，可理解为将AP绕点A逆时针旋转90°得AQ，故Q点轨迹与P点轨迹都是圆．接下来确定圆心与半径．
考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；
考虑AP=AQ，可得Q点轨迹圆圆心M满足AM=AO，且可得半径MQ=PO．
即可确定圆M位置，任意时刻均有△APO≌△AQM．
如图，△APQ是直角三角形，∠PAQ=90°且AP=2AQ，当P在圆O运动时，Q点轨迹是？
【分析】考虑AP⊥AQ，可得Q点轨迹圆圆心M满足AM⊥AO；
考虑AP:AQ=2:1，可得Q点轨迹圆圆心M满足AO:AM=2:1．
即可确定圆M位置，任意时刻均有△APO∽△AQM，且相似比为2．
【模型总结】
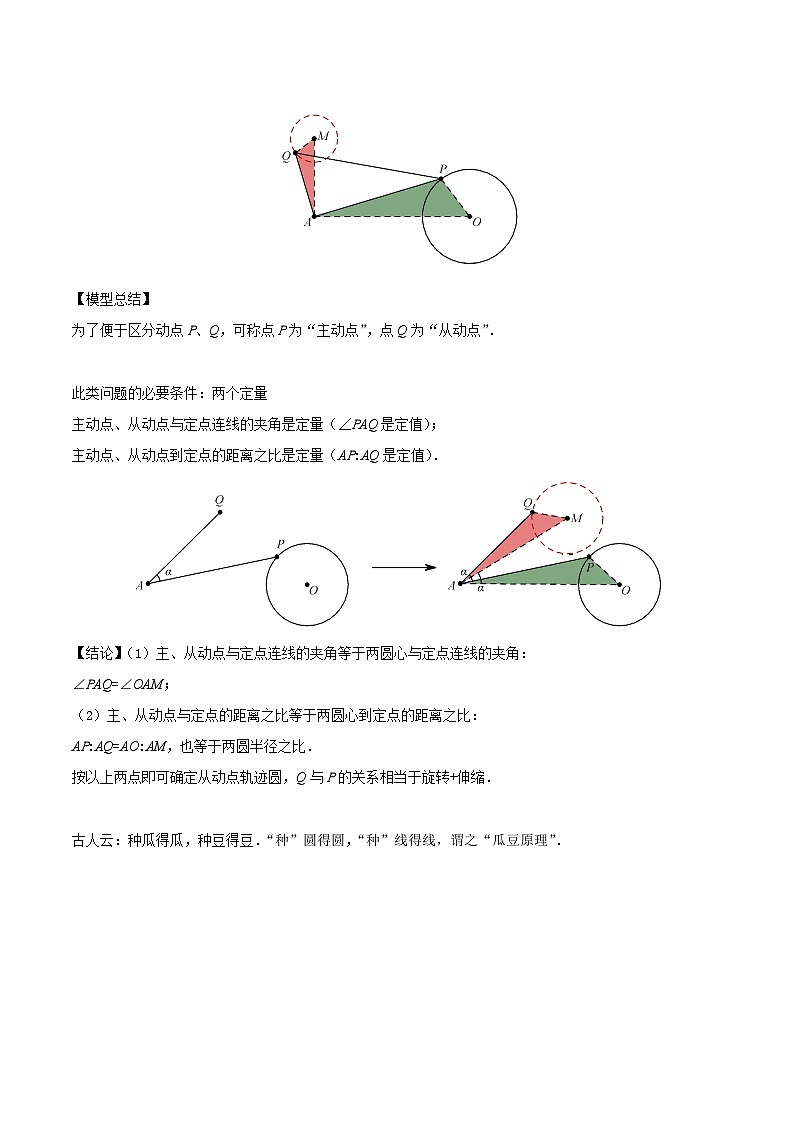
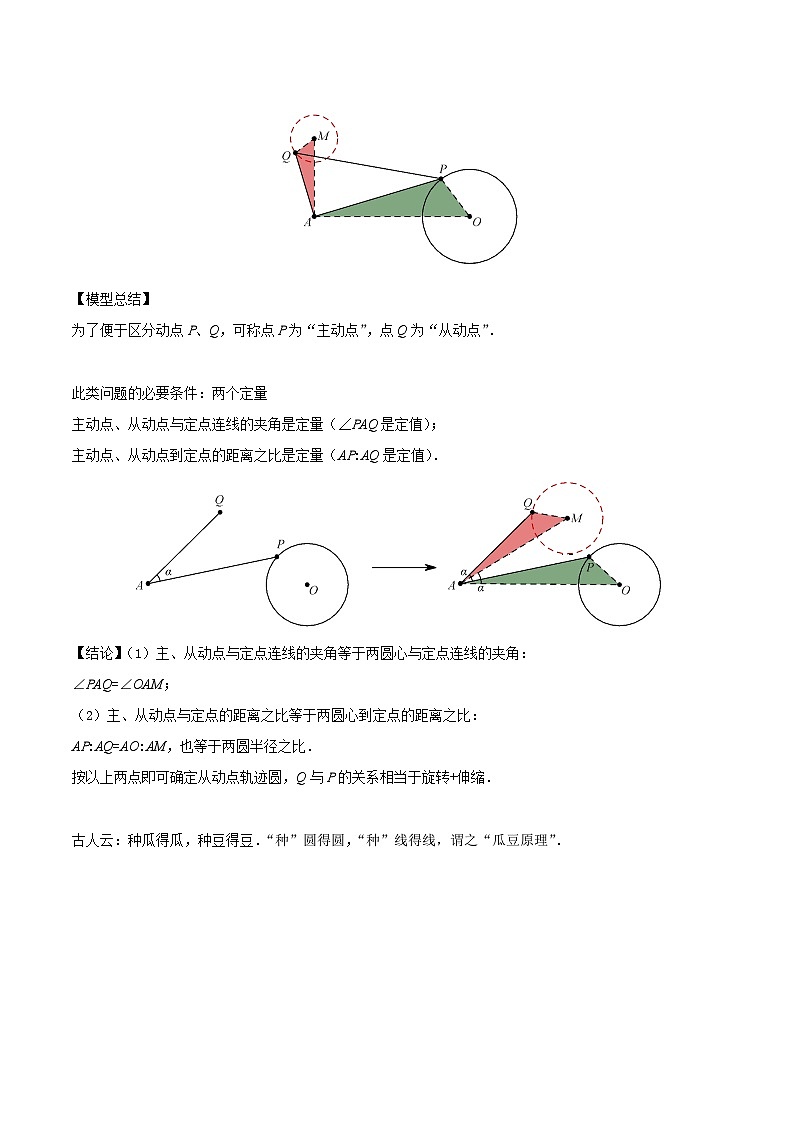
为了便于区分动点P、Q，可称点P为“主动点”，点Q为“从动点”．
此类问题的必要条件：两个定量
主动点、从动点与定点连线的夹角是定量（∠PAQ是定值）；
主动点、从动点到定点的距离之比是定量（AP:AQ是定值）．
【结论】（1）主、从动点与定点连线的夹角等于两圆心与定点连线的夹角：
∠PAQ=∠OAM；
（2）主、从动点与定点的距离之比等于两圆心到定点的距离之比：
AP:AQ=AO:AM，也等于两圆半径之比．
按以上两点即可确定从动点轨迹圆，Q与P的关系相当于旋转+伸缩．
古人云：种瓜得瓜，种豆得豆．“种”圆得圆，“种”线得线，谓之“瓜豆原理”．
【例题】
1、如图，在 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（ ）
A．5B．6C．7D．8
2、如图，在矩形纸片ABCD中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点E是AB的中点，点F是AD边上的一个动点，将 SKIPIF 1 < 0 沿EF所在直线翻折，得到 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的长的最小值是 SKIPIF 1 < 0 SKIPIF 1 < 0
A． SKIPIF 1 < 0 B．3C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3、如图，在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，BC＝2 ，△ADC与△ABC关于AC对
称，点E、F分别是边DC、BC上的任意一点，且DE＝CF，BE、DF相交于点P，则CP的最小值为( )
A．1B．C．D．2
4、如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将ΔEBF沿EF所在直线折叠得到ΔEB' F，连接B' D，则B' D的最小值是_____．
5、如图， SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是 SKIPIF 1 < 0 内部的一个动点，且满足 SKIPIF 1 < 0 ，则线段 SKIPIF 1 < 0 长的最小值为________.
6、如图，点 SKIPIF 1 < 0 在半圆 SKIPIF 1 < 0 上，半径 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在弧 SKIPIF 1 < 0 上移动，连接 SKIPIF 1 < 0 ，作 SKIPIF 1 < 0 ，垂足为 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在移动的过程中， SKIPIF 1 < 0 的最小值是______．
7、如图，过抛物线上一点A作轴的平行线，交抛物线于另一点B，交轴于点C，已知点A的横坐标为．
（1）求抛物线的对称轴和点B的坐标；
（2）在AB上任取一点P，连结OP，作点C关于直线OP的对称点D；
①连结BD，求BD的最小值；
②当点D落在抛物线的对称轴上，且在轴上方时，求直线PD的函数表达式．
【解析】（1）由题意A（﹣2，5），对称轴x=﹣=4，∵A、B关于对称轴对称，∴B（10，5）．
（2）①如图1中，
由题意点D在以O为圆心OC为半径的圆上，
∴当O、D、B共线时，BD的最小值=OB﹣OD=．
②如图2中，
图2
当点D在对称轴上时，在Rt△ODE中，OD=OC=5，OE=4，
∴DE==3，∴点D的坐标为（4，3）．
设PC=PD=x，在Rt△PDK中，x2=（4﹣x）2+22，∴x=，∴P（，5），
∴直线PD的解析式为y=﹣x+．动点的轨迹为定圆时，可利用：“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和，最小值为定点到圆心的距离与半径之差”的性质求解。
确定动点轨迹为圆或者圆弧型的方法:
动点到定点的距离不变，则点的轨迹是圆或者圆弧。
当某条边与该边所对的角是定值时，该角的顶点的轨迹是圆，具体运用如下;
= 1 \* GB3 \* MERGEFORMAT ①见直角，找斜边，想直径，定外心，现圆形
= 2 \* GB3 \* MERGEFORMAT ②见定角，找对边，想周角，转心角，现圆形