天津市第六十一中学2022-2023学年八年级上学期期中数学试卷

这是一份天津市第六十一中学2022-2023学年八年级上学期期中数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

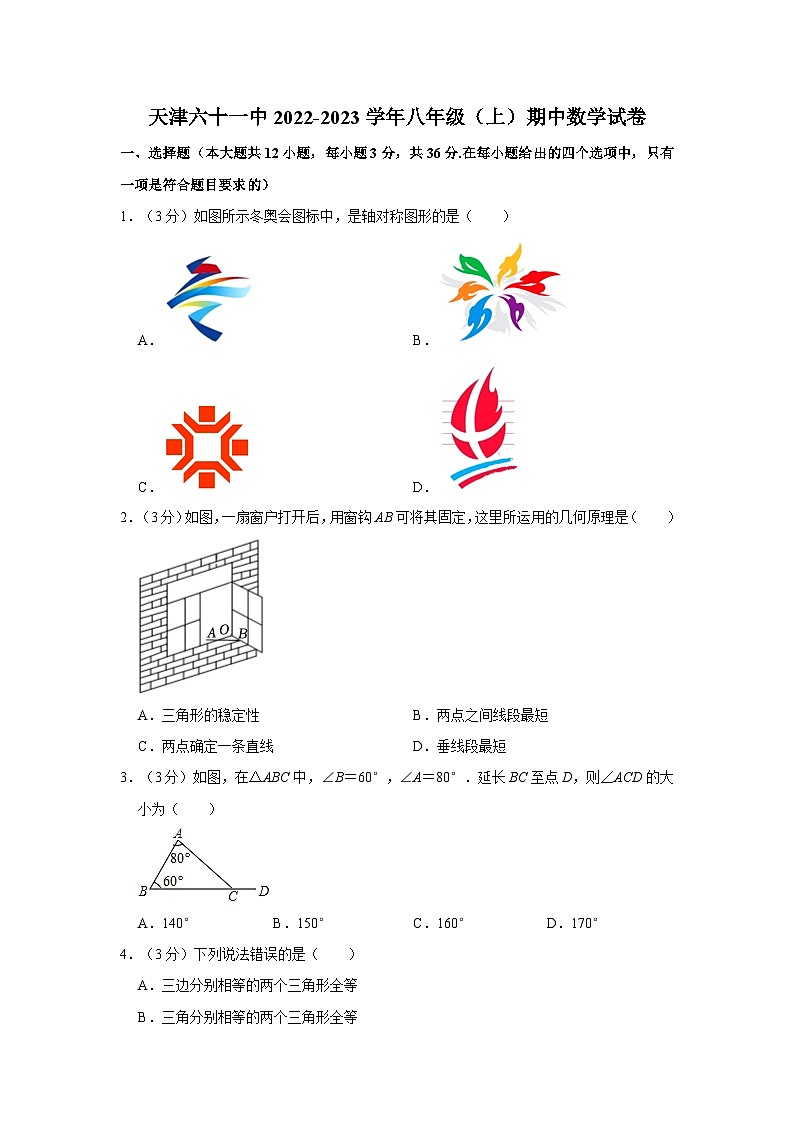
1．（3分）如图所示冬奥会图标中，是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（ ）
A．三角形的稳定性B．两点之间线段最短
C．两点确定一条直线D．垂线段最短
3．（3分）如图，在△ABC中，∠B＝60°，∠A＝80°．延长BC至点D，则∠ACD的大小为（ ）
A．140°B．150°C．160°D．170°
4．（3分）下列说法错误的是（ ）
A．三边分别相等的两个三角形全等
B．三角分别相等的两个三角形全等
C．两边和它们的夹角分别相等的两个三角形全等
D．斜边和一条直角边分别相等的两个直角三角形全等
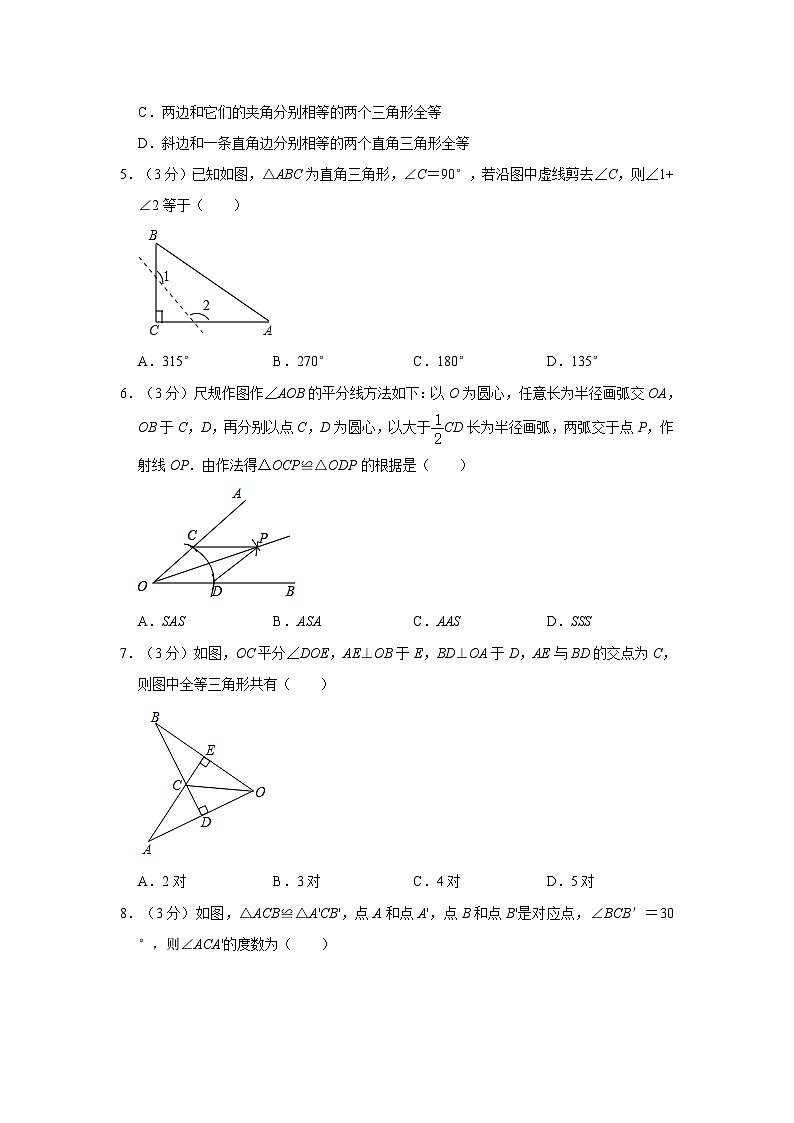
5．（3分）已知如图，△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
A．315°B．270°C．180°D．135°
6．（3分）尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于CD长为半径画弧，两弧交于点P，作射线OP．由作法得△OCP≌△ODP的根据是（ ）
A．SASB．ASAC．AASD．SSS
7．（3分）如图，OC平分∠DOE，AE⊥OB于E，BD⊥OA于D，AE与BD的交点为C，则图中全等三角形共有（ ）
A．2对B．3对C．4对D．5对
8．（3分）如图，△ACB≌△A'CB'，点A和点A'，点B和点B'是对应点，∠BCB′＝30°，则∠ACA'的度数为（ ）
A．20°B．30°C．35°D．40°
9．（3分）如图，BD＝CF，FD⊥BC于点D，DE⊥AB于点E，BE＝CD，若∠AFD＝145°，则∠EDF的度数为（ ）
A．45°B．55°C．35°D．65°
10．（3分）如图，△ABC中，D点在BC上，将D点分别以AB、AC为对称轴，画出对称点E、F，并连接AE、AF，根据图中标示的角度，∠EAF的度数为（ ）
A．126°B．128°C．130°D．132°
11．（3分）如图，在△ABC中，AC＝4cm，线段AB的垂直平分线交AB，AC于点M，N，△BCN的周长是7cm，则BC的长为（ ）
A．4cmB．3cmC．2cmD．1cm
12．（3分）如图，在四边形ABCD中，∠A＝90°，AD＝3，连接BD，BD⊥CD，∠ADB＝∠C．若P是BC边上一动点，则DP长的最小值为（ ）
A．1B．6C．3D．12
二、填空题（本大题共6小题，每小题3分，共18分）
13．（3分）一个多边形的内角和是1080°，这个多边形的边数是 ．
14．（3分）若等腰三角形的一条边长为4cm，另一条边长为9cm，则此三角形第三条边长为 cm．
15．（3分）如图，已知∠1＝∠2，要根据ASA判定△ABD≌△ACD，则需要补充的一个条件为 ．
16．（3分）如图的三角形纸片中，AB＝8，BC＝6，AC＝5，沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△ADE的周长为 ．
17．（3分）如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是 ．
18．（3分）如图，已知∠MON＝80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D．当AB⊥OM，且△ADB有两个相等的角时，∠OAC的度数为 ．
三、解答题（本大题共6小题，共46分.解答应写出文字说明、演算步骤或推理过程）
19．（6分）如图是3×3的正方形网格，每个小正方形的顶点称为格点．A，B两点均为格点，按下列要求画图：在图中，画出所有符合以AB为一边的等腰△ABC，且C为格点．
20．（6分）如图，在△ABC中，∠B＝45°，∠C＝75°，AD是△ABC的角平分线，求∠ADC的度数．
21．（8分）如图，AC＝EF，BC＝DE，A、D、B、F共线，且AD＝BF，求证：△ABC≌△FDE．
22．（8分）如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD交于点O，OB＝OC．求证：∠1＝∠2．
23．（8分）如图，E为△ABC边BC的中点，DE⊥BC，交△ABC的外角∠BAM的平分线于点D，DF⊥AB于F，且AB＞AC．
（1）求证：CD＝BD；
（2）求证：BF＝AC+AF．
24．（10分）如图，在四边形ABCD中，AD＝AB，DC＝BC，∠DAB＝60°，∠DCB＝120°，E是AD上一点，F是AB延长线上一点，且DE＝BF．
（1）求∠D的度数；
（2）求证：CE＝CF；
（3）若G在AB上且∠ECG＝60°，试猜想DE，EG，BG之间的数量关系，并证明．
天津六十一中2022-2023学年八年级（上）期中数学试卷
参考答案
一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．C；2．A；3．A；4．B；5．B；6．D；7．C；8．B；9．B；10．D；11．B；12．C；
二、填空题（本大题共6小题，每小题3分，共18分）
13．8；14．9；15．∠BAD＝∠CAD；16．7；17．30；18．10°、25°、40°；
三、解答题（本大题共6小题，共46分.解答应写出文字说明、演算步骤或推理过程）
19．
解：当以AB为等腰△ABC的腰时，如图，
当以AB为等腰△ABC的底时，如图，
；
20．75°．；
21．
证明：∵AD=FB，
∴AD+DB=FB+DB，即AB=FD．
在△ABC与△FDE中，
⎧
，
∴△ABC≌△FDE（SSS）．
22．证明：∵CD⊥AB于D点，BE⊥AC于点E
∴∠BDO=∠CEO=90°
在△BDO和△CEO中，
，∴△BDO≌△CEO（AAS），
∴OD=OE，
∵OD⊥AB，OE⊥AC，
∴OA平分∠BAC，
∴∠1=∠2．；
；
24．；
，
∴△BFD≌△CND（HL），
∴BF=CN=AC+AN=AC+AF．
（3）（3）EG=BG+DE．，
证明如下：
∵∠DCB=120°，∠ECG=60°，
∴∠DCE+∠BCG=60°，
由（2）知，△CDE≌△CBF，
∴∠DCE=∠BCF，CE=CF，
∴∠DCE+∠BCG=∠BCF+∠BCG=60°，即∠FCG=60°=∠ECG，
在△ECG和△FCG中，，
∴△ECG≌△FCG（SAS），
∴EG=FG=BG+BF=BG+DE，即EG=BG+DE．
；（1）证明：∵E为△ABC边BC的中点，DE⊥BC，
∴CD=BD；
（2）证明：过点D作DN⊥MC于点N，
∵AD为∠BAM角平分线，
∴∠DAN=∠DAF，
∵DN⊥MC，DF⊥AB，
∴∠AFD=∠AND，
在△AFD和△AND中，，
∴△AFD≌△AND（AAS），
∴AF=AN，DF=DN，
∵∠BFD=∠CND=90°，
在Rt△BFD和Rt△CND中，