山东省济南市槐荫区2023-2024学年八年级上学期期中数学测试试卷

这是一份山东省济南市槐荫区2023-2024学年八年级上学期期中数学测试试卷，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．)
1．4的算术平方根是（ ）
A．2B．－2C．±2D．2
2．下列4组数中，不是二元一次方程2x+y＝4的解的是（ ）
A．x=1y=2B．x=2y=0C．x=0.5y=3D．x=−2y=4
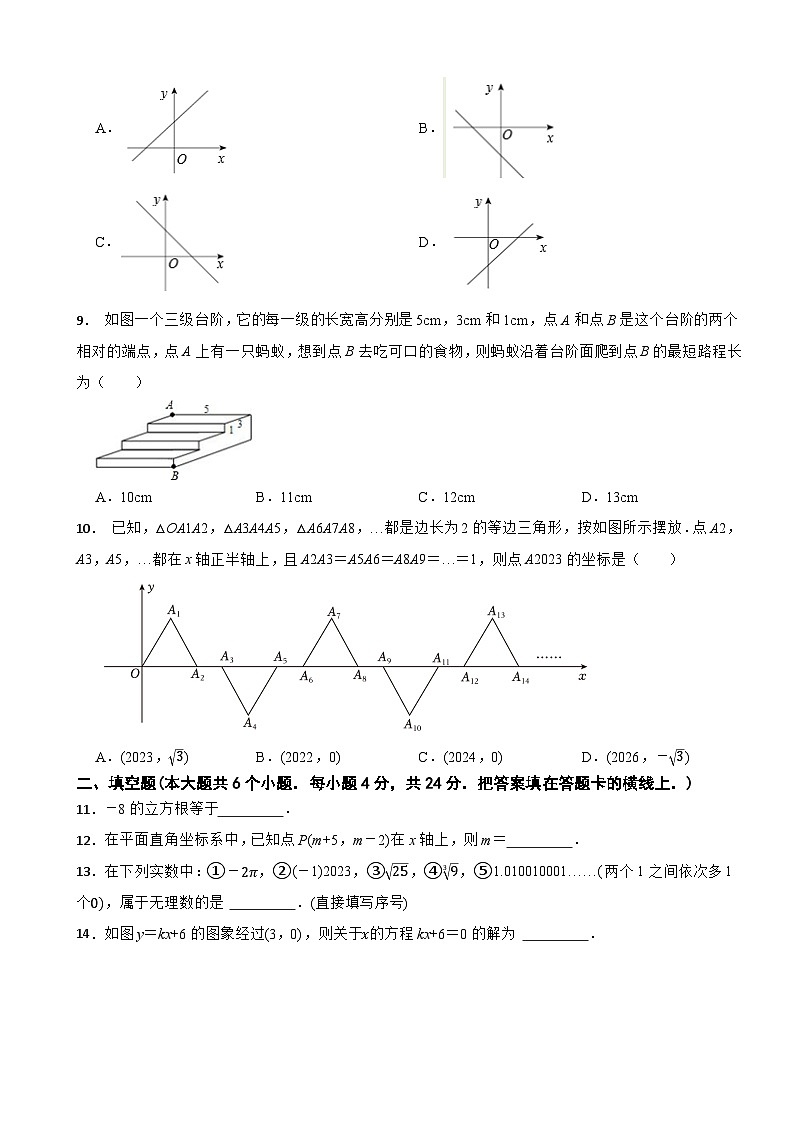
3．下列二次根式中是最简二次根式的是（ ）
A．0.3B．7C．12D．12
4．已知点P在第四象限，且点P到x轴的距离为3，到y轴的距离为4，点P坐标为（ ）
A．(3，－4)B．(－3，4)C．(4，－3)D．(－4，3)
5．估算－17的值（ ）
A．在－6与－5之间B．在－5与－4之间
C．在－4与－3之间D．在－3与－2之间
6．如图所示图象中，表示y是x的函数的有（ ）
A．①②③④B．①②③C．①④D．②③
7．如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线上D′处，若AB＝6，AD＝8，则ED的长为（ ）
A．43B．3C．1D．32
8．若直线y＝kx+b经过第一、二、四象限，则直线y＝bx+k的图象大致是（ ）
A．B．
C．D．
9． 如图一个三级台阶，它的每一级的长宽高分别是5cm，3cm和1cm，点A和点B是这个台阶的两个相对的端点，点A上有一只蚂蚁，想到点B去吃可口的食物，则蚂蚁沿着台阶面爬到点B的最短路程长为（ ）
A．10cmB．11cmC．12cmD．13cm
10． 已知，△OA1A2，△A3A4A5，△A6A7A8，…都是边长为2的等边三角形，按如图所示摆放．点A2，A3，A5，…都在x轴正半轴上，且A2A3＝A5A6＝A8A9＝…＝1，则点A2023的坐标是（ ）
A．(2023，3)B．(2022，0)C．(2024，0)D．(2026，－3)
二、填空题(本大题共6个小题．每小题4分，共24分．把答案填在答题卡的横线上．)
11．－8的立方根等于 ．
12．在平面直角坐标系中，已知点P(m+5，m－2)在x轴上，则m＝ ．
13．在下列实数中：①－2π，②(－1)2023，③25，④39，⑤1.010010001……(两个1之间依次多1个0)，属于无理数的是 ．(直接填写序号)
14．如图y＝kx+6的图象经过(3，0)，则关于x的方程kx+6＝0的解为 ．
15．已知关于x，y的方程组2x+y=2a+1x+2y=a−1的解满足x－y＝6，则a的值为 ．
16．在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中，老师给出了直角坐标系中的三个点：A（0，2），B（2，3），C（3，1）．同学们画出了经过这三个点中每两个点的一次函数的图象，并得到对应的函数表达式y1=k1x+b1，y2=k2x+b2，y3=k3x+b3．分别计算k1+b1，k2+b2，k3+b3的值，其中最大的值等于 ．
三、解答题(本大题共10个小题，共86分．解答应写出文字说明，证明过程或演算步骤．)
17．计算：（18+12）×8
18．解方程组：x−2y=03x−y=5
19．明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地．送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺(AC＝1尺)，将它往前推进两步(EB＝10尺)，此时踏板升高离地五尺(BD＝5尺)，∠OEB=90°.
求秋千绳索(OA或OB)的长度．
20．2023年9月23日至10月8日，第19届亚运会在杭州成功举办，为了更好的发扬亚运精神，济南市某校乒乓球社团购买乒乓球和乒乓球拍，已知甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍，乒乓球每盒定价20元，乒乓球拍每副定价100元．现两家商店都搞促销活动，甲店每买一副球拍赠两盒乒乓球，乙店按八折优惠．社团需购球拍4副，乒乓球x(x≥10)盒．
（1）若在甲店购买付款y甲(元)，在乙店购买付款y乙(元)，分别写出：y甲、y乙与x的函数关系式．
（2）若该社团需要购买乒乓球30盒，在哪家商店购买合算？
21．已知，如图，方格纸中每个小方格都是边长为1个单位长度的正方形，现有A、B、C三点，其中点A坐标为(－4，1)，点B坐标为(1，1)．
⑴请根据点A、B的坐标在方格纸中画出平面直角坐标系，并直接写出点C坐标 ；
⑵作出点C关于直线AB的对称点D．则点D的坐标为 ；
⑶在y轴上找一点F，使△ABF的面积等于△ABD的面积，点F的坐标为 ．
22．因为一次函数y＝kx+b与y＝－kx+b(k≠0)的图象关于y轴对称，所以我们定义：函数y＝kx+b与y＝－kx+b(k≠0)互为“镜子”函数．
（1）请直接写出函数y＝3x－2的“镜子”函数： ；
（2）如果一对“镜子”函数y＝kx+b与y＝－kx+b(k≠0)的图象交于点A，且与x轴交于B、C两点，如图所示，若△ABC是等腰直角三角形，∠BAC＝90°，且它的面积是16，求这对“镜子”函数的解析式．
23．如图，正方形网格中的每个小正方形的边长都是1，点A、B、C均在格点上．
（1）图中线段AB= ，AC= ，BC= ；
（2）判断△ABC的形状，并说明理由；
（3）若AD⊥BC于点D，求AD的长．
24．某型号新能源纯电动汽车充满电后，蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象如图所示．
（1）根据图象，直接写出蓄电池剩余电量为35(千瓦时)时汽车已行驶的路程为 千米；
（2）当0⩽x⩽150时，求1千瓦时的电量汽车能行驶的路程；
（3）当150⩽x⩽200时，求y关于x的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量．
25．如图，△ABC是边长为4的等边三角形，动点E、F均以每秒1个单位长度的速度同时从点A出发，点E沿折线A→B→C方向运动，点F沿折线A→C→B方向运动，当两点相遇时停止运动．设运动的时间为t秒，点E，F的距离为y．
（1）求y关于t的函数关系式并注明自变量t的取值范围；
（2）在给定的平面直角坐标系中，画出这个函数图象，并写出该函数的一条性质；
（3）结合函数图象，直接写出点E，F相距3个单位长度时t的值．
26．如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是22个单位长度，长方形ABCD的长AD是42个单位长度，长方形EFGH的长EH是82个单位长度，点E在数轴上表示的数是52，且E、D两点之间的距离为122．
（1）点H在数轴上表示的数是 ，点A在数轴上表示的数是 ；
（2）若线段AD的中点为M，线段EH上有一点N，EN=14EH，点M以每秒4个单位长度的速度向右匀速运动，点N以每秒3个单位长度的速度向左运动，设运动的时间为x秒，问当x为多少时，原点O恰为线段MN的三等分点？
（3）若线段AD的中点为M，线段EH上有一点N，EN=14EH，长方形ABCD以每秒4个单位长度的速度向右匀速运动，长方形EFGH保持不动，设运动时间为秒，是否存在一个的值，使以M、N、F三点为顶点的三角形是直角三角形？若存在，直接写出的值；不存在，请说明理由．
答案解析部分
1．【答案】A
【知识点】算术平方根
【解析】【解答】解：由题意可得：
4的算术平方根是2
故答案为：A
【分析】根据算术平方根的定义即可求出答案.
2．【答案】D
【知识点】二元一次方程的解
【解析】【解答】解：A：当x=1时，解得：y=2，是方程的解，不符合题意；
B：当x=2时，解得：y=0，是方程的解，不符合题意；
C：当x=0.5时，解得：y=3，是方程的解，不符合题意；
D：当x=-2时，解得：y=8，不是方程的解，符合题意.
故答案为：D
【分析】将方程的解代入方程即可求出答案.
3．【答案】B
【知识点】最简二次根式
【解析】【解答】解：A：0.3=3010，不是最简二次根式，不符合题意；
B：7，是最简二次根式，符合题意；
C：12=23，不是最简二次根式，不符合题意；
D：12=22，不是最简二次根式，不符合题意；
故答案为：B
【分析】根据最简二次根式的定义即可求出答案.
4．【答案】C
【知识点】点的坐标与象限的关系
【解析】【解答】解：由题意可得：
已知点P在第四象限，且点P到x轴的距离为3，到y轴的距离为4，点P坐标为（4，-3）
故答案为：C
【分析】根据第四象限的点的坐标特征即可求出答案.
5．【答案】B
【知识点】无理数的估值
【解析】【解答】解：∵4=16