

广东省汕头市潮南区陈店镇初中学校2023-2024学年九年级上学期期末数学试题
展开一、选择题(每小题3分,共30分)
1.彩民李大叔购买1张彩票,中奖这个事件是( )
A.必然事件B.确定性事件C.不可能事件D.随机事件
2.关于x的二次方程a−1x2+x+a2−1=0的一个根是0,则a的值为( )
A.1B.−1C.1或−1D.12
3.下列图形中,是中心对称图形的是( )
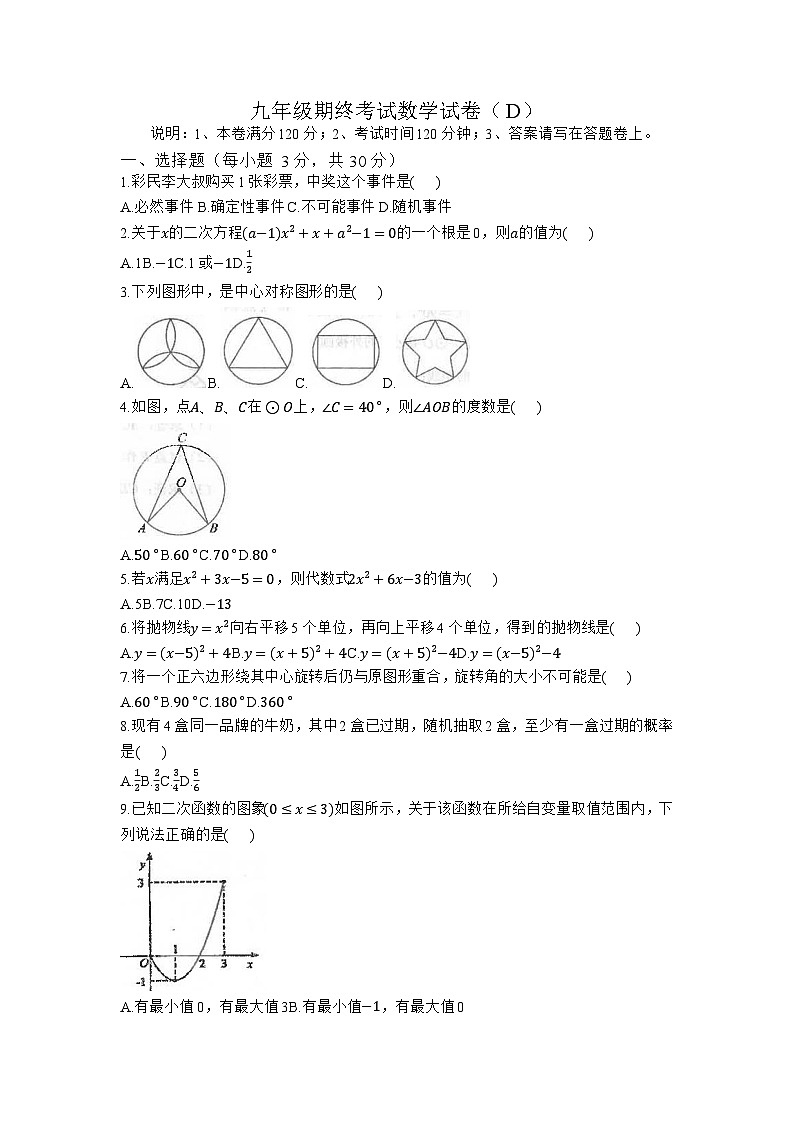
4.如图,点A、B、C在⊙O上,∠C=40∘,则∠AOB的度数是( )
A.50∘B.60∘C.70∘D.80∘
5.若x满足x2+3x−5=0,则代数式2x2+6x−3的值为( )
−13
6.将抛物线y=x2向右平移5个单位,再向上平移4个单位,得到的抛物线是( )
A.y=x−52+4B.y=x+52+4C.y=x+52−4D.y=x−52−4
7.将一个正六边形绕其中心旋转后仍与原图形重合,旋转角的大小不可能是( )
A.60∘B.90∘C.180∘D.360∘
8.现有4盒同一品牌的牛奶,其中2盒已过期,随机抽取2盒,至少有一盒过期的概率是( )
9.已知二次函数的图象0≤x≤3如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3B.有最小值−1,有最大值0
C.有最小值−1,有最大值3D.有最小值−1,无最大值
10.如图,在Rt△ABC,∠C=90∘,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E,若CD=2,则图中阴影部分面积为( )
A.4−π2B.2−π2
C.2−πD.1−π4
二、填空题(每小题3分,共15分)
11.方程x2−5=0的根是 .
12.已知二次函数y=2−kx2,当x>0时,y随x增大而增大,则实数k的取值范围是 .
13.已知扇形的半径为9,弧长为6π,则它的圆心角是 度.
14.如图,在△ABC,∠B=90∘,AB=BC=4,将△ABC绕点A逆时针旋转60∘,得到△ADE,则点D到BC的距离是 .
15.如图,图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑧个图形中菱形的个数为 .
三、解答题(一)(每小题6分,共24分)
16.已知抛物线y=ax2−2ax−8a≠0经过点−2,0,求抛物线解析式和顶点坐标.
17.若实数x,y满足(x2+y2)x2+y2−2=3,求x2+y2的值.
18.如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
19.某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均的每年增长的百分率为x.
(1)用含x代数式表示第3年的可变成本为 万元.
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
四、解答题(二)(每小题7分,共21分)
20.甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋巾随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
21.已知关于x的一元二次方程x2−2x+k−1=0有两个实数根.
(1)求k的取值范围;
(2)设m是方程的一个实数根,且满足m2−2m+3k+4=7,求k的值.
22.如图,点E为正方形ABCD外一点,∠AEB=90∘,将Rt△ABE绕A点逆时针方向旋转90∘得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知BH=7,BC=13,求DH的长.
五、解答题(三)(每小题10分,共30分)
23.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36m2,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大?
最大值为多少?
24.如图,在△ABC,∠C=90∘,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;
(3)求证:CD=HF.
25.如图,抛物线y=ax2+bx+3与x轴交于点A3,0,与y轴交于点B,点C在直线 AB上,过点C作CD⊥x轴于点D1,0 ,将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.
(1)求抛物线解析式;
(2)连接BE,求△BCE的面积;
(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标:若不存在,请说明理由.
九年级期终考试数学试卷(D)
一、选择题(每小题3分,共30分)
二、填空题(每小题3分,共15分)
11.x1=5,x2=−5
12.k<2
13.120∘
14.2
15.73
三、解答题(一)(每小题6分,共24分)
16.解:把−2,0代入y=ax2−2ax−8,得4a+4a−8=0,解得a=1,
∴物线的函数表达式为y=x2−2x−8,
配方得y=x−12−9,
∴顶点坐标为1,−9.
17.解:设x2+y2=t,原方程变形为,tt−2=3,
t2−2t−3=0
t−3t+1=0
∴t1=3,t2=−1
又∵x2+y2≥0,
∴x2+y2=3.
或:x2+y22−2x2+y2−3=0
x2+y2−3x2+y2+1=0
x2+y2=3或x2+y2=−1
又∵x2+y2≥0,
∴x2+y2=3.
18.解:如图所示
⊙P即为所求作的圆.
19.(1)2.61+x2;
(2)由题意,得4+2.61+x2=7.146,
解得:x1=0.1,x2=−2.1.(不合题意,舍去).
答:可变成本平均每年增长的百分率为10%.
四、解答题(二)(每小题7分,共21分)
20.(1)解:三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,∴从袋中随机摸出一球,标号是1的概率为:13;
(2)这个游戏不公平.
画树状图得:
∴共有9种等可能的结果,两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)=59,P(乙胜)=49,∴P(甲胜)≠P(乙胜),
∴这个游戏不公平.
21.(1)解:∵关于x的一元二次方程x2−2x+k−1=0有两个实数根,
∴Δ=−22−4×1×k−1=8−4k≥0,
解得k≤2,答:k的取值范围为k≤2.
(2)∵m是方程x2−2x+k−1=0的一个实数报
∴m2−2m+k−1=0,即m2−2m=1−k
又m2−2m+3k+4=7
∴4−kk+4=7,即k2=9
解得:k1=3,k2=−3
由(1)知k≤2
∴k1=3舍去答:k的值为−3.
22.(1)解:四边形AFHE是正方形,理由如下:
根据旋转性质可得:∠AEB=∠AFD=90∘,
AE=AF,∠EAB=∠DAF
∵四边形ABCD是正方形,
∴∠DAB=90∘
∴∠FAE=∠DAB=90∘
∴∠AEB=∠AFH=∠FAE=90∘
∴四边形AFHE是矩形
又AE=AF
∴四边形AFHE是正方形
(2)连接BD
∵BC=CD=13
∴在Rt△BCD中,BD=CD2+BC2=132
∵四边形AFHE是正方形
∴∠EHD=90∘
又BH=7
∴在Rt△DHB中,DH=BD2−BH2=17
五、解答题(三)(每小题10分,共30分)
23.(1)解:根据题意知:较大矩形的宽为2xm,长为24−x−2x3=8−xm
∴x+2x8−x=36
解得:x1=2,x2=6
又当x=6时,x+2x=18>10不符合题意,舍去
∴x=2
答:此时x的值为2m;
(2)解:设矩形养殖场的总面积为S,
由(1)得:S=3x8−x=−3x−42+48,
∵墙的长度为10,
∴0<3x≤10,
∴0
∴x<4时:S随着x的增大而增大,
∴当x=103时,S有最大值,最大值为−3×103−42+48=1403m2,
答:当x=103时,矩形养殖场的总面积最大,最大值为1403m2.
24.(1)证明:如图,连接OE.
∵BE⊥EF,∴∠BEF=90∘,
∴BF是圆O的直径,
∴OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠CBE=∠OBE,∴∠OEB=∠CBE,
∴OE//BC,
∴∠AEO=∠C=90∘,
∴AC是⊙O的切线:
(2)∵∠C=∠BHE=90∘,∠EBC=∠EBA,
∴BEC=∠BEH,
∵BF是⊙O是直径,
∴∠BEF=90∘,
∴∠FEH+∠BEH=90∘,∠AEF+∠BEC=90∘,
∴∠FEH=∠FEA,
∴FE平分∠AEH.
(3)如图,连结DE.
∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,
∴EC=EH.
∵∠CDE+∠BDE=180∘,∠HFE+∠BDE=180∘,
∴∠CDE=∠HFE,
∵∠C=∠EHF=90∘,
∴△CDE≅△HFEAAS,
∴CD=HF,
25.(1)解:∵△ACD沿CD所在直线翻折,点A落在点E处,A3,0,D1,0
∴E−1,0
∵点A、点E都在抛物线y=ax2+bx+3上
∴{9a+3b+3=0a−b+3=0,解得{a=−1b=2
∴抛物线的解析式为y=−x2+2x+3
(2)∵抛物线y=−x2+2x+3与y轴交于点B
∴当x=0时,y=3∴B0,3 设直线AB的解析式为y=kx+bk≠0
把A、B两点的坐标代入得{3k+b=0b=3,解得{k=−1b=3
∴直线AB的解析式为y=−x+3
∵点C在直线AB上,CD⊥x轴于点D1,0
当x=1时,y=−1+3=2
∴C1,2
∴AE=4,OB=3,CD=2
∴S△BCE=S△ABE−SACF=12×4×3−12×4×2=2
答:△BCE的面积为2.
(3)抛物线上存在一点P,使∠PEA=∠BAE,
∵A3,0,B0,3
∴OA=OB=3
∴△AOB为等腰直角三角形,则有∠BAE=45∘
∵点P在抛物线上
∴设点P的坐标为m,−m2+2m+3
①当点P在x轴上方时记为P1,过P1做P1M⊥x轴于点M
在Rt△EMP1中,∵∠P1EA=∠BAE=45∘
∴EM=P1M,即m+1=−m2+2m+3,
解得:m1=2,m2=−1(舍去)
当m=2时,−m2+2m+3=3
∴点P1的坐标为2,3
②当点P在x轴下方时记为P2过P2做P2N⊥x轴于点N
在R1△ENP2中,即∵∠P2EN=∠BAE=45∘
∴EN=P2N,即m+1=−−m2+2m+3,
解得:m1=4,m2=−1(舍去)
当m=4时,−m2+2m+3=−5
∴点P2的坐标为4,−5
综上,符合条件的P点坐标是2,3或4,−5.
广东省汕头市潮南区陈店镇初中七校联考2023-2024学年七年级上学期1月期末数学试题: 这是一份广东省汕头市潮南区陈店镇初中七校联考2023-2024学年七年级上学期1月期末数学试题,共6页。
广东省汕头市潮南区陈店镇初中学校2023-2024学年九年级上学期12月期末数学试题: 这是一份广东省汕头市潮南区陈店镇初中学校2023-2024学年九年级上学期12月期末数学试题,共9页。
广东省汕头市潮南区陈店镇初中七校联考2023—-2024学年七年级上学期11月期中数学试题: 这是一份广东省汕头市潮南区陈店镇初中七校联考2023—-2024学年七年级上学期11月期中数学试题,共25页。












