河南省开封市五县2022-2023学年高三下学期开学考试理科数学试题（Word版附解析）

这是一份河南省开封市五县2022-2023学年高三下学期开学考试理科数学试题（Word版附解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 已知集合，，则（ ）
A. B. C. D.
【答案】D
【解析】
【分析】求出集合中元素范围，再求即可.
【详解】，，
故选：D.
2. 已知复数是纯虚数，则（ ）
A. 3B. 1C. D.
【答案】B
【解析】
【分析】求出复数的代数形式，再根据纯虚数的概念列式计算.
【详解】,
因为复数是纯虚数，
则，解得
故选：B.
3. 古代名著《九章算术》中记载了求“方亭”体积的问题，方亭是指正四棱台，今有一个方亭型的水库，该水库的下底面的边长为20km，上底面的边长为40km，若水库的最大蓄水量为，则水库深度（棱台的高）为（ ）
A. 10mB. 20m
C. 30mD. 40m
【答案】A
【解析】
【分析】由题意可知：该水库是一个正四棱台，已知正四棱台的体积为，上下底面边长分别为40km和20km，求正四棱台的高，同一单位，代入体积计算公式即可求解.
【详解】因为正四棱台上下底面边长分别为40km和20km，设高，
因为，，由棱台的体积计算公式可得：
，解得：，
故选：.
4. 已知抛物线C：，过焦点F的直线与C在第四象限交于M点，则（ ）
A. 3B. 4C. 5D. 6
【答案】C
【解析】
【分析】由题意可知：焦点坐标为，设点，利用直线的斜率可得，再利用抛物线的定义即可求解.
【详解】因为直线过抛物线C：的焦点，则，
所以，，抛物线方程为，因为在抛物线上且在第四象限，设点，则，解得：，由抛物线的定义可知：，
故选：
5. 记为等差数列的前项和，已知，，则（ ）
A. 3B. C. 2D.
【答案】D
【解析】
【分析】设等差数列的公差为，利用已知求出即得解.
【详解】解：设等差数列的公差为，所以
所以.
故选：D
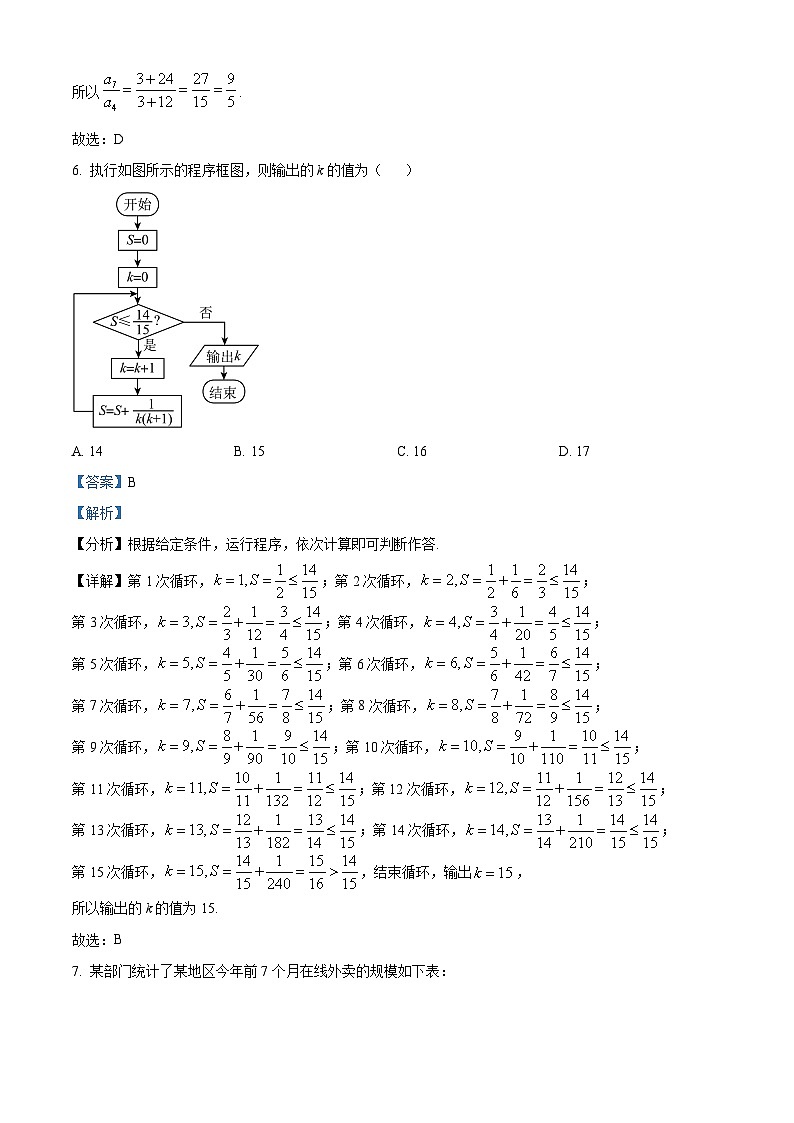
6. 执行如图所示的程序框图，则输出的k的值为（ ）
A. 14B. 15C. 16D. 17
【答案】B
【解析】
【分析】根据给定条件，运行程序，依次计算即可判断作答.
【详解】第1次循环，；第2次循环，；
第3次循环，；第4次循环，；
第5次循环，；第6次循环，；
第7次循环，；第8次循环，；
第9次循环，；第10次循环，；
第11次循环，；第12次循环，；
第13次循环，；第14次循环，；
第15次循环，，结束循环，输出，
所以输出的k的值为15.
故选：B
7. 某部门统计了某地区今年前7个月在线外卖的规模如下表：
其中4、6两个月的在线外卖规模数据模糊，但这7个月的平均值为23．若利用回归直线方程来拟合预测，且7月相应于点的残差为，则（ ）
A. 1.0B. 2.0C. 3.0D. 4.0
【答案】B
【解析】
【分析】根据给定条件，求出，再借助回归直线的特征及残差列出方程组即可求解作答.
【详解】依题意，，而，于是得，
而当时，，即，联立解得，
所以.
故选：B
8. 已知的展开式中的系数为，则实数（ ）
A. B. C. D.
【答案】A
【解析】
【分析】利用二项式定理可分别得到和展开式的通项，令即可讨论得到的取值，结合展开式通项，利用的系数构造方程即可求得的值.
【详解】展开式的通项为：，且；
展开式的通项为：，且；
令，则或，
的系数为，
解得：.
故选：A.
9. 记函数的最小正周期为T，若，且函数的图象关于点对称，则当取得最小值时，（ ）
A. 2B. 1C. －1D. －2
【答案】D
【解析】
【分析】由及的图象关于对称列出关系式，求出，，再由的图象关于对称可求的最小值，从而可求的值．
【详解】由已知得，
因为函数的图象关于对称，所以，
所以，所以，
又因为，所以，，
由的图象关于对称得，
所以，即有，
又因为，所以当最小时，，此时，
所以，
故选：D．
10. 已知曲线在点处的切线与轴交于点，曲线在点处的切线与轴交于点，若，则的取小值为（ ）
A B. C. D.
【答案】C
【解析】
【分析】设，，求导，，根据导数的几何意义结合，得，求出切线方程，得到的坐标，由两点间的距离公式和基本不等式可求出结果.
【详解】设，，
，，
因为，所以，得，
，令，得，则，
，令，得，则，
则+
，两次不等式取等的条件都是.
所以的取小值为.
故选：C
11. 已知是双曲线：的右焦点，为坐标原点，是的右支上一点，若，，则的离心率为（ ）
A. B. C. D. 2
【答案】A
【解析】
【分析】利用双曲线性质可得，根据余弦函数的定义求出，根据双曲线定义求出，在中运用余弦定理即可求解.
【详解】如图所示：
其中为双曲线的左焦点，则有，，
，，且，
即，所以，
在中，，
由双曲线定义知，，解得，
在中，，
则有，化简得，所以.
故选：A.
12. 已知函数，的定义域为，且，，若为偶函数．，则（ ）
A. 24B. 26C. 28D. 30
【答案】B
【解析】
【分析】根据已知等式，结合偶函数的性质可以判断出函数的周期，利用周期进行求解即可.
【详解】由，而，
所以可得，因为为偶函数，
所以，显然有，
所以函数的周期为8，
在中，令，得，
因为，
所以，
由，
由，所以
故选：B
【点睛】关键点睛：根据偶函数的性质、结合已知等式赋值求出函数的周期是解题的关键.
二、填空题：本题共4小题，每小题5分，共20分.
13. 已知向量，若，则实数a＝___.
【答案】
【解析】
【详解】，由，得，解得.
14. 写出与圆和都相切的一条直线的方程___________．
【答案】（答案不唯一）
【解析】
【分析】根据给定圆的方程，判断两圆的位置关系，再写出一条公切线方程作答.
【详解】圆的圆心，半径，圆的圆心，半径，
则，因此圆相外切，它们有3条公切线，而轴，，
则两圆的每条公切线斜率都存在，设公切线方程为，为常数，
于是得，整理得或，
解得，解得：或，
因此圆的公切线方程为：或或，
所以与圆和都相切的一条直线的方程可以为.
故答案为：
15. 已知球的半径为2，四棱锥的顶点均在球的球面上，当该四棱锥的体积最大时，其高为______
【答案】##
【解析】
【分析】根据圆的几何性质、球的几何性质，结合导数的性质、棱锥的体积公式进行求解即可.
【详解】圆内接四边形是正方形时，这个四边形的面积最大，当四棱锥的高经过点时，此时体积最大，如图所示：
设此时正方形的边长为，所以，
设该四棱锥的高为，所以有，
由勾股定理可得：，
该四棱锥的体积为，
设，
当时，单调递增，当时，单调递减，
所以当时，函数有最大值.
故答案为：.
【点睛】关键点睛：根据导数的性质是解题的关键.
16. 现取长度为2的线段的中点，以为直径作半圆，该半圆的面积为（图1），再取线段的中点，以为直径作半圆．所得半圆的面积之和为（图2），再取线段的中点，以为直径作半圆，所得半圆的面积之和为，以此类推，则______．
【答案】
【解析】
【分析】先求得，然后利用错位相减求和法求得正确答案.
【详解】依题意，，
，
，
以此类推可知，数列是首项为，公比是的等比数列，
所以.
令，
则，
，
两式相减得

所以.
所以.
故答案为：
三、解答题：共70分.解答应写出文字说明，证明过程或演算步骤，第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.
（一）必考题：共60分.
17. 已知内角A，B，C的对边分别为a，b，c，．
（1）证明：为定值；
（2）若，，求的周长．
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）利用正弦定理角化边以及余弦定理可整理变形得到为定值；
（2）先利用（1）以及余弦定理求出，然后再次用余弦定理并利用变形可得，则周长可求.
【小问1详解】
即，
由正弦定理角化边以及余弦定理得
，
整理得，即，
所以为定值；
【小问2详解】
由（1），
，
，
得，
的周长为
18. 青少年近视问题备受社会各界广泛关注，某研究机构为了解学生对预防近视知识的掌握程度，对某校学生进行问卷调查，并随机抽取200份问卷，发现其得分（满分：100分）都在区间中，并将数据分组，制成如下频率分布表：
（1）试估计这200份问卷得分的平均值（同一组中的数据用该组区间的中点值代表）；
（2）用样本估计总体，用频率估计概率，从该校学生中随机抽取4人深入调查，设X为抽取的4人中得分在的人数，求的分布列与数学期望．
【答案】（1）
（2）答案见解析
【解析】
【分析】（1）先利用频率和为1求出，在利用平均值的公式求解即可；
（2）由题可得服从二项分布，根据二项分布的公式以及期望公式计算可得答案.
【小问1详解】
由频率分布表可得，解得，
所以这200份问卷得分的平均值为
；
【小问2详解】
由题意可得的可能取值为，则，
又，
则的分布列为：
19. 在四棱锥中，底面，，，，，．
（1）证明：平面平面；
（2）若，求二面角的余弦值．
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）根据勾股定理得，由底面，得，根据线面垂直的判定定理得平面，再根据面面垂直的判定定理得平面平面；
（2）以为原点，所在直线为轴，过垂直于平面的直线为轴，建立空间直角坐标系，利用二面角的向量公式可求出结果.
小问1详解】
因为，，，所以，
又因为，．所以，即，
因为底面，底面，所以，
由，，平面，平面，，得平面，
又因为平面，所以平面平面；
【小问2详解】
以为原点，所在直线为轴，过垂直于平面的直线为轴，建立如图所示的空间直角坐标系：
则，，，，
在平面中，如图：
，，，所以，
，，，所以，
所以，
过作，垂足为，则，即，
又，所以，即，，
所以，，
所以，
则，，，
设平面的一个法向量为，
则，则，令，得，则，
设平面的一个法向量为，
则，令，得，，得，
.
根据图形可知，二面角为锐角，
所以二面角的余弦值为.
20. 已知椭圆E的中心为坐标原点O，对称轴分别为x轴、y轴，且过，两点．
（1）求E的方程；
（2）设F为椭圆E的一个焦点，M，N为椭圆E上的两动点，且满足，当M，O，N三点不共线时，求△MON的面积的最大值．
【答案】（1）
（2）
【解析】
【分析】(1)将给定点代入设出的方程求解即可；
(2)根据题意可得：，进而得到直线斜率，设直线的方程，与曲线方程联立，利用韦达定理和弦长公式求出，再利用点到直线的距离公式求出点到直线的距离，进而求出面积的最值.
【小问1详解】
设椭圆方程为，因为椭圆过点，，
所以，解得：，所以椭圆的方程为：.
【小问2详解】
不妨设为椭圆的下焦点，由(1)可知：点，则，
因为，则，所以，
设直线的方程为：，，
联立方程组，整理可得：，则，即（*），
由韦达定理可得：，，
由弦长公式可得：，
点到直线的距离，
所以，
所以当时，的面积最大，最大为.
21. 已知函数（）．
（1）讨论的单调性；
（2）若，（）是的两个极值点，证明：．
【答案】（1）当时，在区间上单调递增；
当时，在区间和上单调递增，在区间上单调递减；
当时，在区间上单调递增，在区间上单调递减.
（2）证明见解析.
【解析】
【分析】（1）对求导，根据的取值范围，对的符号进行讨论，即可得出的单调性；
（2）由第一问中有两个极值点时，和化简不等式，然后构造函数，利用导数研究所构造函数的单调性，根据单调性进行证明.
【小问1详解】
∵，（）∴定义域为，
∴，（），
令，（），
①当时，，，，，
此时，在区间上单调递增；
②当时，，
令，解得，，
∴当时，，，
当时，，，
∴此时，在区间上单调递增，在区间上单调递减；
③当时，，
（i）当时，，，，，
∴此时，在区间上单调递增；
（ii）当时，，
令，解得，，且，
∴当时，，，
当时，，，
∴此时，在区间和上单调递增，
在区间上单调递减.
综上所述，当时，在区间上单调递增；
当时，在区间和上单调递增，
在区间上单调递减；
当时，在区间上单调递增，在区间上单调递减.
【小问2详解】
由第（1）问知，若，（）是的两个极值点，
则，且的两根即为，，
且，，∴，
，
∴，
又∵，
∴不等式等价于，
∵，∴，，又∵，∴，
∴不等式又等价于，即，
∴只需证，
令，，则，在区间上单调递减，
又∵，∴，，
∴，
∴若，（）是的两个极值点，.
【点睛】利用导数证明不等式的常用方法有构造函数法和放缩法，
（1）构造函数法
①直接构造函数：若需要证明（或），可通过构造函数，转化为证明（或）；
②化简构造函数：若原不等式较为复杂，或者构造函数后，通过导数判断函数的单调性较为困难，可以将原不等式适当化简变形后再构造函数.
本题第（2）问的证明，就是综合了以上两种方法.
（2）放缩法：通常会利用常见结论放缩或结合已知条件进行放缩.
（二）选考题：共10分，请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.
[选修：坐标系与参数方程]
22. 在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点,轴正半轴为极轴建立极坐标系，已知直线的极坐标方程为．
（1）求曲线的普通方程；
（2）若与有两个不同公共点，求的取值范围．
【答案】（1）
（2）
【解析】
【分析】（1）在曲线的参数方程中消去参数，可得出曲线的普通方程，利用基本不等式求出的取值范围，即可得解；
（2）求出直线的普通方程，分析可知直线与双曲线的右支有两个交点，将直线与双曲线方程联立，利用直线与双曲线的位置关系可得出关于的不等式组，即可解得实数的取值范围.
【小问1详解】
解：由可得，即，
因为，则，当且仅当时，等号成立，
故曲线的普通方程为.
【小问2详解】
解：因为直线的极坐标方程为，
所以，直线的普通方程为，
联立可得，
设直线与曲线交于点、，
由题意可得，解得.
因此，实数的取值范围为.
[选修4－5：不等式选讲]
23. 已知函数．
（1）求不等式的解集；
（2）设函数，若对任意，都存在，使得成立，求实数a的取值范围．
【答案】（1）；
（2）.
【解析】
【分析】（1）化函数为分段函数，再分段解不等式作答.
（2）求出函数、的值域，再借助集合的包含关系求解作答.
【小问1详解】
依题意，函数，则不等式化为：
或或，解得或或，则，
所以不等式的解集为.
【小问2详解】
由（1）知，当时，，当时，，当时，，
因此函数的值域为，
，，当且仅当时取等号，
因此函数的值域为，
因为对任意，都存在，使得成立，则有，
即，解得，
所以实数a的取值范围是.月份代号x
1
2
3
4
5
6
7
在线外卖规模y（百万元）
11
13
18
★
28
★
35
分数
频率
0.15
0.25
0.30
0.10