




2024年中考数学常见几何模型全归纳之模型解读与提分精练(全国通用)专题32圆中的重要模型之隐圆模型
展开
这是一份2024年中考数学常见几何模型全归纳之模型解读与提分精练(全国通用)专题32圆中的重要模型之隐圆模型,文件包含专题32圆中的重要模型之隐圆模型原卷版docx、专题32圆中的重要模型之隐圆模型解析版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
模型1、动点定长模型(圆的定义)
若P为动点,且AB=AC=AP,则B、C、P三点共圆,A圆心,AB半径
圆的定义:平面内到定点的距离等于定值的所有点构成的集合.
寻找隐圆技巧:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧.
例1.(2023·山东泰安·统考中考真题)如图,在平面直角坐标系中,的一条直角边在x轴上,点A的坐标为;中,,连接,点M是中点,连接.将以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段的最小值是( )
A.3B.C.D.2
例2.(2023·广东清远·统考三模)如图,在,,E为边上的任意一点,把沿折叠,得到,连接.若,,则的最小值为 .
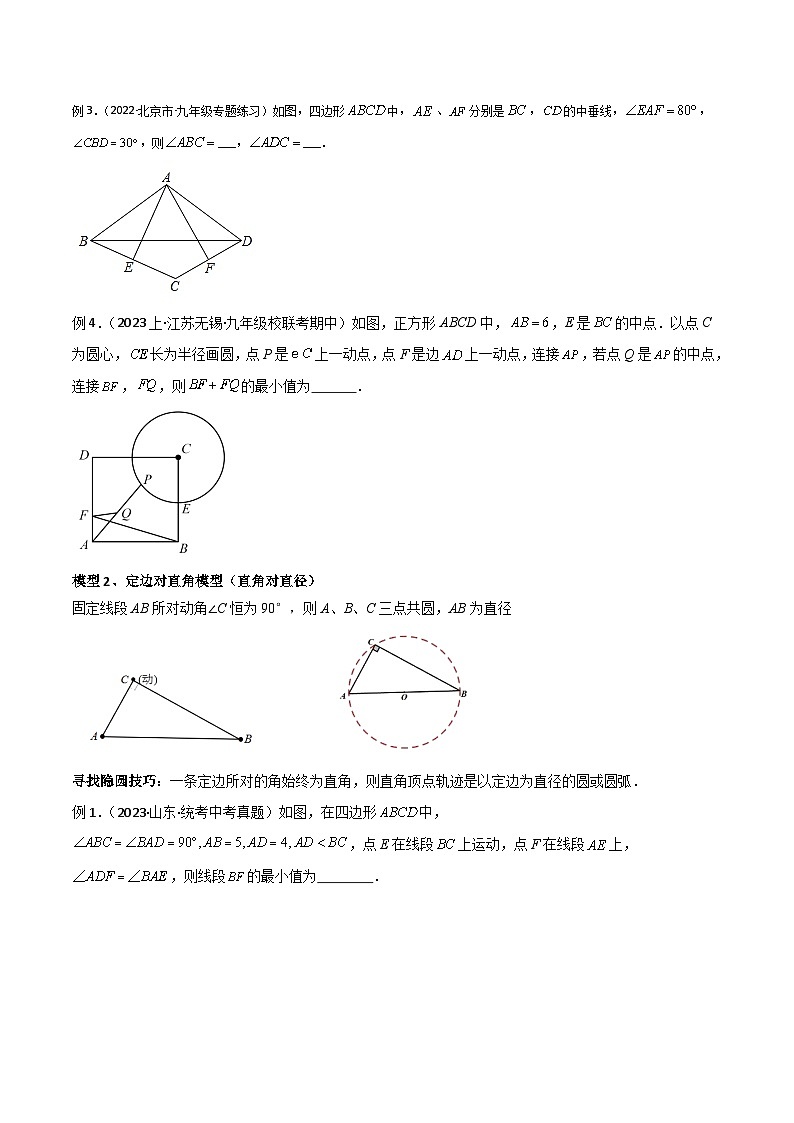
例3.(2022·北京市·九年级专题练习)如图,四边形中,、分别是,的中垂线,,,则___,___.
例4.(2023上·江苏无锡·九年级校联考期中)如图,正方形ABCD中,,E是的中点.以点C为圆心,长为半径画圆,点P是上一动点,点F是边上一动点,连接,若点Q是的中点,连接,,则的最小值为 .
模型2、定边对直角模型(直角对直径)
固定线段AB所对动角∠C恒为90°,则A、B、C三点共圆,AB为直径
寻找隐圆技巧:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.
例1.(2023·山东·统考中考真题)如图,在四边形中,,点E在线段上运动,点F在线段上,,则线段的最小值为 .
例2.(2023上·江苏苏州·九年级校考阶段练习)如图,以为圆心,半径为2的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为上一动点,作于点F.当点E从点B出发,顺时针旋转到点D时,点F所经过的路径长为( )
A.B.C.D.
例3.(2022·内蒙古·中考真题)如图,是的外接圆,为直径,若,,点从点出发,在内运动且始终保持,当,两点距离最小时,动点的运动路径长为______.
例4.(2023·广东·九年级课时练习)如图,△ACB中,CA=CB=4,∠ACB=90°,点P为CA上的动点,连BP,过点A作AM⊥BP于M.当点P从点C运动到点A时,线段BM的中点N运动的路径长为( )
A.πB.πC.πD.2π
模型3、定边对定角模型(定弦定角模型)
固定线段AB所对同侧动角∠P=∠C,则A、B、C、P四点共圆
根据圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角都相.
寻找隐圆技巧:AB为定值,∠P为定角,则P点轨迹是一个圆.
1.(2023·四川自贡·统考中考真题)如图,分别经过原点和点的动直线,夹角,点是中点,连接,则的最大值是( )
A.B.C.D.
例2.(2023·广东深圳·校考模拟预测)如图,在边长为6的等边中,点E在边上自A向C运动,点F在边上自C向B运动,且运动速度相同,连接交于点P,连接,在运动过程中,点P的运动路径长为( )
A.B.C.D.
例3.(2023·成都市·九年级专题练习)如图所示,在扇形中,,,点是上的动点,以为边作正方形,当点从点移动至点时,求点经过的路径长.
例4.(2023上·湖北武汉·九年级校考阶段练习)如图,⊙O的半径为2,弦AB的长为2,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为 .
模型4、四点共圆模型
四点共圆模型我们在上一专题中已经详细讲解了,本专题就不在赘述了。在此就针对几类考查频率高的模型作相应练习即可。
1)若平面上A、B、C、D四个点满足,则A、B、C、D四点共圆.
条件:1)四边形对角互补;2)四边形外角等于内对角.
2)若平面上A、B、C、D四个点满足,则A、B、C、D四点共圆.
条件:线段同侧张角相等.
例1.(2023·安徽阜阳·九年级校考期中)如图,O为线段的中点,点A,C,D到点O的距离相等,则∠A与∠C的数量关系为( )
A.B.C.D.
例2.(2023·山西临汾·九年级统考期末)如图在四边形中,,若,则的值为( )
A.B.C.D.
例3.(2023·江苏镇江·校联考一模)如图,菱形的边长为,,点为边的中点.点从点出发,以每秒个单位的速度向点运动,点同时从点出发,以每秒个单位的速度向点运动,连接,过点作于点.当点到达点时,点也停止运动,则点的运动路径长是( )
A.B.12C.D.
例4.(2023.江苏九年级期末)如图,在中,,,,点P为平面内一点,且,过C作交PB的延长线于点Q,则CQ的最大值为( )
A.B.C.D.
例5.(2023·河南周口·校考三模)在中,,M是外一动点,满足,若,,,则的长度为 .
课后专项训练
1.(2023上·江苏南通·九年级校考阶段练习)如图,等边三角形ABC与等边三角形EFB共端点B,BC=2,BF=,△EFB绕点B旋转,∠BCF的最大度数( )
A.30°B.45°C.60°D.90°
2.(2023上·安徽六安·九年级校考期末)如图,是等边三角形,,点是内一点,且,连接,则的最小值为( )
A.B.C.D.
3.(2023·广西·中考模拟)如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为( )
A. B. C. D.
4.(2023上·浙江杭州·九年级校联考期中)如图,点在线段上,,以为圆心,为半径作,点在上运动,连接,以为一边作等边,连接,则长度的最小值为( )
A.B.C.D.
5.(2023上·江苏无锡·九年级校联考期中)如图,在平面直角坐标系中,点A,C,N的坐标分别为,,,以点C为圆心,3为半径画,点P在上运动,连接,交于点Q,点M为线段的中点,连接,则线段的最小值为( )
A.7B.10C.D.
6.(2023上·浙江丽水·九年级统考期中)如图,是半圆的直径,点在半圆上,是弧上的一个动点,连结,过点点作于点,连结,在点移动的过程中.(1) ;(2)的最小值是 .
7.(2023上·山东日照·九年级校考期中)如图,中,,过点作的平行线为直线上一动点,为的外接圆,直线交于点,则的最小值为 .
8.(2023上·江苏连云港·九年级校考期中)如图,在矩形中,,N是矩形内一点,,点M是边上的动点,则的最小值为 .
9.(2023.湖北九年级期中)如图,在中,,,,点在以为直径的半圆上运动,由点运动到点,连接,点是的中点,则点经过的路径长为 .
10.(2023·广东·九年级课时练习)如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 ________.
11.(2023上·江苏连云港·九年级统考期中)如图,在矩形中,已知,,点是边上一动点点不与点,重合,连接,作点关于直线的对称点,连接,则的最小值为 .
12.(2023上·江苏连云港·九年级统考期中)如图,在等腰直角三角形中,,,点是边上一动点,连结,以为直径的圆交于点,则长度的最小值是 .
13.(2023·辽宁大连·九年级统考期末)如图,在中,,D为AB上一点,,E为AC上一点,,连接BE、CD交于点O,则的最大面积是 .
14.(2021·广东·统考中考真题)在中,.点D为平面上一个动点,,则线段长度的最小值为 .
15.(2023·浙江·一模)如图,在中,,.分别以、为斜边,向三角形外作等腰直角三角形和等腰直角三角形,则和面积之和为 ;连接,则线段的最大值为 .
16.(2022·广东·九年级专题练习)如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD=2,E是AC的中点,连接DE,则线段DE长度的最小值为______.
17.(2023陕西中考模拟)如图,在等边中,,点P为AB上一动点,于点D,于点E,则DE的最小值为_____.
18.(2023上·江苏宿迁·九年级统考期中)如图1,点是直径上一点,,,过点作弦,点在上运动,连接.(1)求的长.(2)如图,连接,作的角平分线交于点,在点运动的过程中,的长度是否会发生变化?若发生变化,请说明理由;若不会发生变化,请求出其值.(3)如图,过点作于,连接,求的最小值.
19.(2023下·广东广州·九年级校校考阶段练习)如图,为等边三角形,点P是线段上一动点(点P不与A,C重合),连接,过点A作直线的垂线段,垂足为点D,将线段绕点A逆时针旋转得到线段,连接,.(1)求证:;(2)连接,延长交于点F,若的边长为2;①求的最小值;②求的最大值.
20.(2023·陕西延安·九年级统考期末)问题提出
(1)如图①,内接于半径为4的,是的中位线,则的最大值是_________;
问题探究(2)如图②,在等腰中,,,边上的中线,求等腰外接圆的半径;
问题解决(3)如图③,工人师傅现要在一张足够大的板材上剪裁出一个形状为的部件,已知的部件要满足,边上的中线,且边与边之和要最大,是否能剪裁出满足要求的三角形部件?若能,请求出的最大值;若不能,请说明理由.
相关试卷
这是一份专题07 三角形中的重要模型-等积模型-2024年中考数学常见几何模型全归纳之模型解读与提分精练(全国通用),文件包含专题07三角形中的重要模型-等积模型原卷版docx、专题07三角形中的重要模型-等积模型解析版docx等2份试卷配套教学资源,其中试卷共78页, 欢迎下载使用。
这是一份专题18 全等与相似模型之十字模型-2024年中考数学常见几何模型全归纳之模型解读与提分精练(全国通用),文件包含专题18全等与相似模型之十字模型原卷版docx、专题18全等与相似模型之十字模型解析版docx等2份试卷配套教学资源,其中试卷共77页, 欢迎下载使用。
这是一份专题16 全等与相似模型-半角模型-2024年中考数学常见几何模型全归纳之模型解读与提分精练(全国通用),文件包含专题16全等与相似模型-半角模型原卷版docx、专题16全等与相似模型-半角模型解析版docx等2份试卷配套教学资源,其中试卷共76页, 欢迎下载使用。









