专题强化训练三 向量与立几25道必刷解答题-高二数学《考点•题型 •技巧》精讲与精练高分突破（人教A版2019选择性必修第一册）

这是一份专题强化训练三 向量与立几25道必刷解答题-高二数学《考点•题型 •技巧》精讲与精练高分突破（人教A版2019选择性必修第一册），共36页。

（1）求证：；
（2）若的大小为，求的正弦值．
2．如图，已知四棱锥的底面是菱形，交于，平面，为的中点，点在上，．
（1）证明：平面；
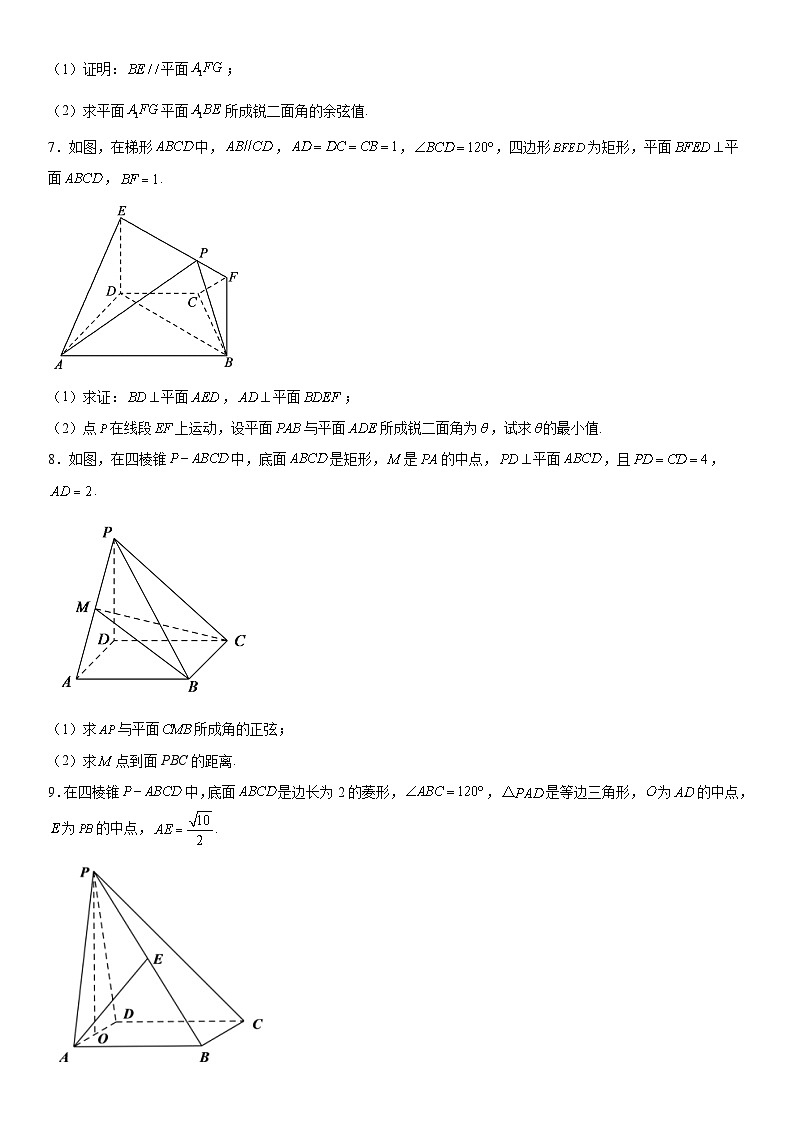
（2）若，求二面角的余弦值．
3．如图，四边形是直角梯形，∥，，，，平面，为的中点．
（1）求证：直线平面；
（2）若三棱锥的体积为，求二面角的正弦值．
4．如图，在四棱柱中，侧棱底面，，，，，且点和分别为和的中点.
（1）求证：平面；
（2）求二面角的正弦值；
（3）求点到平面的距离；
（4）设为棱上的点，若直线和平面所成角的正弦值为，求线段的长.
5．如图，在四棱锥中，底面，四边形中，，.
（1）求证：平面平面；
（2）设，若直线与平面所成角大小为30°，求线段的长.
6．如图1，在等腰中，，D，E分别为，的中点，F为的中点，G在线段上，且.，将沿折起，使点A到的位置（如图2所示），且.
（1）证明：平面；
（2）求平面平面所成锐二面角的余弦值.
7．如图，在梯形中，，，，四边形为矩形，平面平面，.
（1）求证：平面，平面；
（2）点在线段上运动，设平面与平面所成锐二面角为，试求的最小值.
8．如图，在四棱锥中，底面是矩形，是的中点，平面，且，.
（1）求与平面所成角的正弦；
（2）求点到面PBC的距离.
9．在四棱锥中，底面是边长为2的菱形，，是等边三角形，为的中点，为的中点，.
（1）求证：平面.
（2）求平面与平面所成锐角的余弦值.
10．如图所示，在等腰梯形中，，，，，平面，．
（1）求证：平面；
（2）若为线段上一点，且，是否存在实数，使平面与平面所成锐二面角为？若存在，求出实数；若不存在，请说明理由．
11．如图，在四棱锥中，底面是矩形，平面，，，是中点.
（1）求直线与平面的夹角余弦值；
（2）求平面和平面的夹角的余弦值；
（3）求点到平面的距离.
12．如图1，在边长为4的菱形ABCD中，∠BAD＝60，DEAB于点E，将△ADE沿DE折起到△A1DE的位置，使A1DDC，如图2.
（1）求证：A1E平面BCDE；
（2）求二面角E—A1B—C的余弦值.
13．如图，四棱锥中，底面是梯形，，，是等边三角形，是棱的中点，，.
（1）证明：平面；
（2）求直线与平面所成角的正弦值.
14．如图，在多面体中四边形是正方形，平面，平面，．
（1）证明：平面平面．
（2）求平面与平面所成锐二面角的余弦值．
15．如图所示，在四棱锥中，平面，，，，为的中点．
（1）求证平面；
（2）若点为的中点，线段上是否存在一点，使得平面平面？若存在，请确定的位置；若不存在，请说明理由．
16．如图1，在平面四边形ABCD中，BC⊥AC，CD⊥AD，∠DAC=∠CAB=，AB=4，点E为AB的中点，M为线段AC上的一点，且ME⊥AB.沿着AC将△ACD折起来，使得平面ACD⊥平面ABC，如图2.
（1）求证∶BC⊥AD；
（2）求二面角A-DM-E的余弦值.
17．如图，在底面为矩形的四棱锥中，为棱上一点，底面．
（1）证明：；
（2）若，，求二面角的大小．
18．如图在四棱锥中，底面为正方形，为等边三角形，E为中点，平面平面.
（1）求证：平面；
（2）求二面角的余弦值.
19．如图，在四棱锥中，平面平面，底面四边形为直角梯形，，，，，为线段的中点，过的平面与线段，分别交于点，.
（1）求证：；
（2）若为棱上靠近点的三等分点，求直线与平面所成角的正弦值.
20．如图①，在直角梯形中，，，，的是的中点，是与的交点．将沿折起到的位置，如图②．
（1）证明：平面；
（2）若平面平面，求平面与平面夹角的余弦值．
21．如图，为圆锥的顶点，是圆锥底面的圆心，为底面直径，．是底面的内接正三角形，为上一点，．
（1）证明：平面；
（2）求二面角的余弦值．
22．如图，已知三棱柱，平面平面,，分别是的中点.
（1）证明：；
（2）求直线与平面所成角的余弦值.
23．如图，在四棱锥P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且．
（Ⅰ）求证：CD⊥平面PAD；
（Ⅱ）求二面角F–AE–P的余弦值；
（Ⅲ）设点G在PB上，且．判断直线AG是否在平面AEF内，说明理由．
24．（2017新课标全国Ⅲ理科）如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．
（1）证明：平面ACD⊥平面ABC；
（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.
25．如图，三棱柱中，侧面，已知，，，点是棱的中点.
（1）求证：平面；
（2）求二面角的余弦值；
（3）在棱上是否存在一点，使得与平面所成角的正弦值为，若存在，求出的值；若不存在，请说明理由.
参考答案
1．
（1）取的中点，连接，，，如图，
因为正三角形，则，又底面是菱形，且，则是正三角形，于是得，
而，平面，则平面，又平面，
所以；
（2）由(1)知的平面角为，即，，
显然平面平面，在平面内过作，平面平面，则平面，
如图，以为原点建立空间直角坐标系，
则，，，，，
，，，
设平面的法向量为，则，令，得，
设平面的法向量为，则，令，得，
，
设的大小为，从而得，
所以的正弦值为.
2．
（1）设交于，连结，因为，分别是，的中点，则G为的重心，所以，易知O为AC的中点 ，所以．又因为，所以，所以∥，又因为平面，平面，所以∥平面．
（2）如图，以为原点，OA，OB，OP分别为，，轴，建立空间直角坐标系．
设．在菱形中，因为，所以是等边三角形，故．
又因为，平面，所以．
所以，，，，
所以，，，
设平面（即平面）的一个法向量为，由，取，则.
设平面PAB（即平面FAB）的一个法向量为，由，
取a=1，则.
所以．
由图可知，二面角为锐角，所以二面角的余弦值为．
3．
（1）取的中点，连接，，又∵是的中点，∴∥，.
∵∥，，
∴∥，且，
∴四边形是平行四边形，
∴∥，
∵平面，平面，
∴∥平面.
（2）∵AB∥DC，AB⊥AD，
∴∠ADC=90°，由AB=AD=1，则，且∠ADB=45°，
∴∠BDC=45°，
∵DC=2，则在中，由余弦定理：，∴，
∴，∴BD⊥BC.
又底面，设，
则，解得，
∵E为PC的中点，∴.
∴以为原点，为轴，为轴，建立空间直角坐标系，如图所示：
则，，，，，，.
设平面的一个法向量为，则，令y=1，则.
设平面的一个法向量为，则，令b=1，则.
∴，∴二面角的平面角的正弦值为.
4．
【详解】
（1）证明：以点为坐标原点建立空间直角坐标系如图所示，
则，，，，，，，，
因为，分别为，的中点，
则，，
由题意可知，是平面的一个法向量，
又，
所以，
又平面，
故平面；
（2）解：由（1）可知，，，，
设平面的法向量为，
则，
令，则，
故，
设平面的法向量为，
则，
令，则，
故，
所以，
故二面角的正弦值为；
（3）解：因为，，，
设平面的法向量为，
则，
令，则，
故，
所以，
设点到平面的距离为，
则，
所以点到平面的距离为；
（4）解：由题意，设，其中，
则，
所以，
又时平面的一个法向量，
因为直线和平面所成角的正弦值为，
则，
整理可得，
又，解得或（舍），
故线段的长为.
5．
（1）证明：底面，平面，
又，且，平面，
又平面，所以平面平面；
（2）如图以为原点，以，，所在直线为轴建立空间坐标系，
在底面内，作交于E，则，
在直角中，
设，则，，
由，则，则，，，
所以，，
设平面的法向量为，得，
取，则
故由直线与平面所成角大小为30°，则有，
即，化简得：，
解得：或（舍去，因为），即.
6．
解：（1）证明：取的中点M，连接，∵，∴G为的中点，
又F为的中点，所以，
由，，∴平行四边形，
∴，所以，又平面，如图，
所以平面；
（2）根据题意，以F为原点，直线为x轴，过F平行于的直线为y轴，直线为z轴，建立如图空间直角坐标系，
则，
，，，，
设平面的法向量为，
由，得，故，
设平面的法向量，
由，得，故，
∴，
故平面与平面所成锐二面角的余弦值为.
7．
解：（1）证明，在梯形中，
∵，，，
∴，，∴，∴.
∵平面平面，平面平面，平面，，
又∵，∴平面.
又四边形是矩形，∴，∴平面，∴，
∵，∴平面.
（2）由（1）可建立直线，，为轴，轴，轴的如图所示的空间直角坐标系，令，则，，，，
∴，.
设为平面的法向量，由，得，
取，则.
∵是平面的一个法向量，∴.
∵，∴当时，有最大值，∴的最小值为.
8．
（1）因为底面是矩形，平面，
所以以为原点，分别为轴，建立空间直角坐标系，如图所示：
，，，，，
，，，
设平面的法向量，
则，令，即，
设与平面所成角为，
则
（2），，
设平面的法向量，
则，令，即，
设点到面PBC的距离为，
则
9．
（1）连接，.在四棱锥中，底面是边长为2的菱形，且，
∴是边长为2的等边三角形，又是等边三角形，∴是等腰三角形.
∵为的中点，∴，又，，
∴由勾股定理得，∴，
又由，都是边长为2的等边三角形，可知，
∴，∴，
由为等边三角形，为的中点，可知.
又∵，平面，平面.∴平面.
（2）以为坐标原点，分别以，，所在直线为、、轴建立空间直角坐标系，
则，，，，，，
∴，，，.
设平面的法向量为，则，即，
令，则，，∴.
设平面的法向量为，
则，即.令，则，，∴.
设平面与平面所成锐角为，则，
平面与平面所成锐角的余弦值为.
10．
（1）因为，，所以四边形ACFE为平行四边形，所以．
在等腰梯形ABCD中，，，所以，
所以．
又平面ABCD，所以BC，平面BCF，
所以平面BCF．
因为，所以平面BCF；
依题意，以C为坐标原点，分别以直线为x轴、y轴、z轴建立如图所示的空间直角坐标系，
所以，，设
所以 设为平面MAB的法向量，
由得取，所以
因为是平面ABC的一个法向量，设平面MAB与平面ABC所成的锐二面角为，
所以．因为，所以，
所以
所以存在使平面MAB与平面ABC所成锐二面角为．
11．
因为平面，且四边形是矩形，所以两两垂直，
所以分别以所在的直线为轴建立如图所示空间直角坐标系：
（1），，，，
所以，，
设平面的法向量为，
由可得，取则，，
所以，
记直线和平面的夹角为.
则，
所以，
（2）由图可知，平面即平面.
所以平面的法向量为
记面和面的夹角为.
则
由图可知面和面夹角为锐角
所以；
（3），，平面的法向量为
设点到平面的距离为，则，
所以点到平面的距离为.
12．
解:（1）证明:∵在菱形ABCD中，∠BAD＝60，DEAB于点E
∴，，∴.
又∵，，
∴平面，∴.
又∵，，
∴平面.
（2）∵平面，，
∴以，，所在直线分别为轴，轴和轴，建立空间直角坐标系（如图）.
易知，则，，，，
∴，，
易知平面的一个法向量为.
设平面的法向量为，
由，，得，令，得，
∴.
由图得二面角为钝二面角，
∴二面角的余弦值为.

13．
（1）证明：因为，，所以四边形是平行四边形，
所以.在等边中，是中点，，所以.
在中，，所以，所以.
又因为，，所以平面.
（2）解法一：因为平面，所以三棱锥的体积为
.
设点到平面的距离为，又，所以三棱锥的体积为
.
由，得，所以.
设直线与平面所成的角为，则，
所以直线与平面所成角的正弦值为.
解法二：因为平面，，所以，以为原点，分别以射线，，为，，轴的正方向，建立如图所示的空间直角坐标系，则，，，，
，，.
设平面的一个法向量为.
由得取，得.
设直线与平面所成角为，则.
所以直线与平面所成角的正弦值为.
14．
（1）证明：因为平面，平面，所以．
因为平面，平面，所以平面．
因为四边形是正方形，所以．
因为平面，平面，所以平面．
因为平面，平面，且，
所以平面平面．
（2）解：由题意可知，，两两垂直，则以D为原点，分别以，，的方向为x，y，z轴的正方向，建立如图所示的空间直角坐标系．
设，则，，，，从而，．
设平面的法向量为，则，令，得．
平面的一个法向量为．故，
即平面与平面所成锐二面角的余弦值为．
15．
（1）因为平面，所以，又，，所以平面，又，所以面，面，．
又，为的中点，所以，而，所以平面．
（2）以A为坐标原点，所在方向分别为x,y,z轴正方向建立空间直角坐标系，如图，则，，，，，，．
所以，设（），所以，则，所以，，
设平面的法向量为，则，，
即，令，则，
由（1）可知为平面的一个法向量，若平面平面，则，即，解得．
即时平面平面.
16．
（1）∵平面ACD⊥平面ABC.平面ACD∩平面ABC=AC，BC⊥AC，
∴BC⊥平面ACD，∵AD平面ACD，∴BC⊥AD.
（2）根据题意，以C为原点，CA，CB所在直线分别为x，y轴建立如图的空间直角坐标系，
∵BC⊥AC，CD⊥AD，∠DAC=∠CAB=，AB=4，
∴BC=2，AC=，CD=，CM=AC-AM=.
∴，
∴，，
设平面MDE的法向量为，则，即，令，得y=3，z=-1，∴，
由（1）知，平面MAD的一个法向量为=（0，2，0），
∴.
∴二面角A-DM-E的余弦值为.
17．
（1）因为四边形为矩形，则，
平面，平面，则，
，平面，
平面，因此，；
（2）平面，不妨以点为坐标原点，、所在直线分别为、轴建立空间直角坐标系，如下图所示：
、、、，
设平面的法向量为，，，
由，取，可得，
设平面的法向量为，，
由，取，可得，
所以，，
由图可知，二面角的平面角为钝角，
因此，二面角的大小为.
18．
（1）连接交于点O，连接、，
因为为等边三角形，所以，
因为底面为正方形，所以，
因为，所以平面，
又平面，所以，
因为平面平面，平面平面，
所以平面，
因为E为中点，所以，则平面.
（2）如图，以分别为x轴，y轴，z轴正方向建立空间直角坐标系，设，则，
所以，，，，
则，，，
因为平面平面，且平面平面=BD，,
所以面EBD,
所以平面的法向量为，
设平面的法向量为，则，
所以，不妨设x=1，所以，
所以，
显然二面角的平面角为锐角或直角，
所以二面角的余弦值为.
19．
（1）∵，，为的中点，∴且，
∴四边形为平行四边形，
∴，∵平面，平面，∴平面，
∵平面，平面平面，∴.
（2）∵，∴，
∵平面平面，平面平面，平面，
∴平面，分别以，，所在的直线为，，轴，
建立直角坐标系，如图所示，
则，，，，，
∴，，，
设平面的法向量为，则，，
即，令，则，
∴直线与平面所成角的正弦值.
20．
（1）在题图①中，因为，，是的中点，，
所以，即在题图②中，，，又，
所以平面．
又，
所以四边形是平行四边形，
所以，所以平面．
（2）由已知，平面平面，又由（1）知，，，
所以为二面角的平面角，
所以．
如图，以为原点，分别以，，所在直线为轴、轴、轴建立空间直角坐标系．
因为，，
所以，，，，
则，，．
设平面的一个法向量为，
平面的一个法向量为，
平面与平面的夹角为．
则即可取；
即可取．
从而，
即平面与平面夹角的余弦值为．
21．
（1）由题设，知为等边三角形，设，
则，，所以，
又为等边三角形，则，所以，
，则，所以，
同理，又，所以平面；
（2）过O作∥BC交AB于点N，因为平面，以O为坐标原点，OA为x轴，ON为y轴建立如图所示的空间直角坐标系，
则，
，，，
设平面的一个法向量为，
由，得，令，得，
所以，
设平面的一个法向量为
由，得，令，得，
所以
故，
设二面角的大小为，则.
22．
(1)如图所示，连结，
等边中，，则，
平面ABC⊥平面，且平面ABC∩平面，
由面面垂直的性质定理可得：平面，故，
由三棱柱的性质可知，而，故，且，
由线面垂直的判定定理可得：平面，
结合⊆平面，故.
(2)在底面ABC内作EH⊥AC，以点E为坐标原点，EH,EC,方向分别为x,y,z轴正方向建立空间直角坐标系.
设，则，,，
据此可得：，
由可得点的坐标为，
利用中点坐标公式可得：，由于，
故直线EF的方向向量为：
设平面的法向量为，则：
，
据此可得平面的一个法向量为，
此时，
设直线EF与平面所成角为，则.
23．
(Ⅰ)由于PA⊥平面ABCD，CD平面ABCD，则PA⊥CD，
由题意可知AD⊥CD，且PA∩AD=A，
由线面垂直的判定定理可得CD⊥平面PAD.
(Ⅱ)以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD,AP方向为y轴，z轴建立如图所示的空间直角坐标系，
易知：，
由可得点F的坐标为，
由可得，
设平面AEF的法向量为：，则
，
据此可得平面AEF的一个法向量为：，
很明显平面AEP的一个法向量为，
，
二面角F-AE-P的平面角为锐角，故二面角F-AE-P的余弦值为.
(Ⅲ)易知，由可得，
则，
注意到平面AEF的一个法向量为：，
其且点A在平面AEF内，故直线AG在平面AEF内.
24．
（1）由题设可得，，从而.
又是直角三角形，所以.
取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO.
又由于是正三角形，故.
所以为二面角的平面角.
在中，.
又，所以，
故.
所以平面ACD⊥平面ABC.
（2）由题设及（1）知，两两垂直，以为坐标原点，的方向为轴正方向，为单位长，建立如图所示的空间直角坐标系.则.
由题设知，四面体ABCE的体积为四面体ABCD的体积的，从而E到平面ABC的距离为D到平面ABC的距离的，即E为DB的中点，得.
故.
设是平面DAE的法向量，则即
可取.
设是平面AEC的法向量，则同理可取.
则.
所以二面角D-AE-C的余弦值为.
25．
（1）由题意，因为，，，∴，
又∴，∴，
∵侧面，∴.
又∵，，平面
∴直线平面.
（2）以为原点，分别以，和的方向为，和轴的正方向建立如图所示的空间直角坐标系，
则有，，，，
设平面的一个法向量为
，
∵，∴，令，则，∴
设平面的一个法向量为，，，
∵，∴，令，则，∴，
，，，∴.
设二面角为，则.
∴设二面角的余弦值为.
（3）假设存在点，设，∵，，
∴，∴∴
设平面的一个法向量为，
∴，得.
即，∴或，∴或.
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjmath加入百度网盘群4000G一线老师必备资料一键转存自动更新永不过期