



2023-2024学年重庆市永川中学高一上学期期中数学复习题(一)含答案
展开一、单选题
1. 设集合,,,则( )
A. B. C. D.
2. 已知a,b,,则下列语句能成为“a,b,c都不小于1”的否定形式的是( )
A. a,b,c中至少有1个大于1B. a,b,c都小于1
C. a,b,c不大于1D. 或或
3. 若,,则“”是“”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
4. 已知,且,若恒成立,则实数取值范围是 ( )
A. B. C. D.
5. 已知关于x的不等式的解集为,其中,则的最小值为( )
A. B. 2C. 1D.
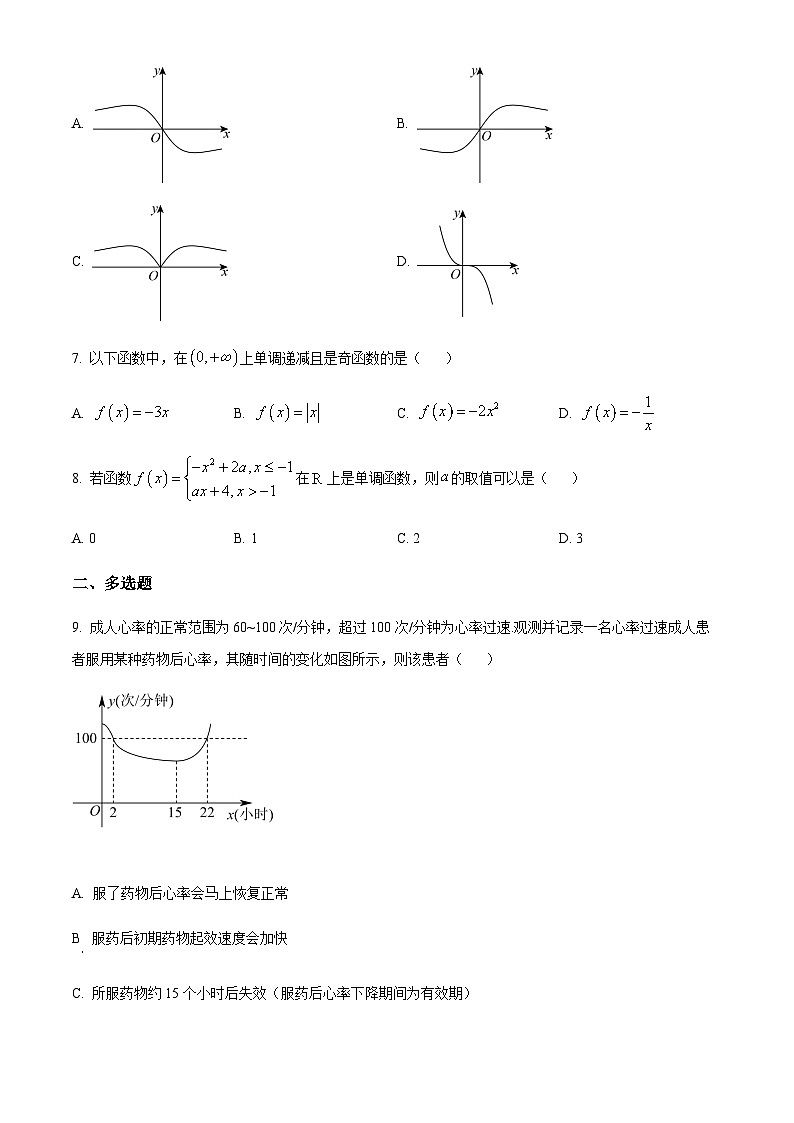
6. 函数的图像大致是( )
A. B.
C. D.
7. 以下函数中,在上单调递减且是奇函数的是( )
A. B. C. D.
8. 若函数在上是单调函数,则的取值可以是( )
A. 0B. 1C. 2D. 3
二、多选题
9. 成人心率的正常范围为60~100次/分钟,超过100次/分钟为心率过速.观测并记录一名心率过速成人患者服用某种药物后心率,其随时间的变化如图所示,则该患者( )
A. 服了药物后心率会马上恢复正常
B 服药后初期药物起效速度会加快
C. 所服药物约15个小时后失效(服药后心率下降期间为有效期)
D. 一天需服用该药1至2次
10. 若函数为上的偶函数,在上单调,且满足对任意,都有,则的值可能为( )
A. 4B. 6C. 7D. 10
11. 下列说法正确的是( )
A. 若幂函数的图象经过点,则解析式为
B. 若函数,则在区间上单调递减
C. 幂函数始终经过点和
D. 若幂函数图像关于轴对称,则
12. 已知是定义域为R函数,为奇函数,为偶函数,则下列说法一定正确的是( )
A. 为奇函数B. 为关于对称
C. 关于点对称D.
三、填空题
13. 设集合,若是的子集,我们把中所有元素的和称为的容量(规定空集的容量为0),若的容量为奇(偶)数,则称为的奇(偶)子集.则的所有奇子集有个______.
14. 对任意,给定,,记函数,则的最小值是__________.
15. 若定义在上的偶函数满足:对任意的,,有,且,则满足的x的取值范围为______.
16. 已知函数,若是幂函数,且是奇函数,试写出一个符合条件的函数______________.
四、解答题
17. 已知集合或,.
(1)若,求实数m的取值范围;
(2)若,且,求实数m的取值范围.
18. 已知命题:“,使得”为真命题.
(1)求实数m的取值的集合A;
(2)设不等式的解集为B,若是的必要不充分条件,求实数a的取值范围.
19. 已知二次函数满足,且.
(1)求的解析式;
(2)解关于的不等式.
20. 函数是定义在上的奇函数,且.
(1)求解析式;
(2)证明在上为增函数;
(3)解不等式.
21. 党的十九大报告明确要求继续深化国有企业改革,培育具有全球竞争力的世界一流企业.某企业抓住机遇推进生产改革,从单一产品转为生产A、B两种产品,根据市场调查与市场预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②(注:所示图中的横坐标表示投资金额,单位为万元).
(1)分别求出A、B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少?
22. 已知函数对任意实数m、n都满足等式,当时,,且.
(1)判断的奇偶性;
(2)判断的单调性,求在区间上的最大值;
(3)是否存在实数a,对于任意,,使得不等式恒成立.若存在,求出a的取值范围;若不存在,请说明理由.
重庆市永川中学校2023-2024学年高一上学期入学考试数学试卷(含答案): 这是一份重庆市永川中学校2023-2024学年高一上学期入学考试数学试卷(含答案),共9页。试卷主要包含了选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年重庆市永川中学高一上学期期中数学模拟题(四)含答案: 这是一份2023-2024学年重庆市永川中学高一上学期期中数学模拟题(四)含答案,文件包含重庆市永川中学2023-2024学年高一上学期半期考试数学模拟题四Word版含解析docx、重庆市永川中学2023-2024学年高一上学期半期考试数学模拟题四Word版无答案docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
2023-2024学年重庆市永川中学校高一上学期10月月考数学试题含答案: 这是一份2023-2024学年重庆市永川中学校高一上学期10月月考数学试题含答案,共13页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












