与圆有关的位置关系复习课课件

这是一份与圆有关的位置关系复习课课件，共38页。PPT课件主要包含了与圆有关的位置关系，点在圆外dr，点在圆上dr，点在圆内d＜r，直线和圆相交，直线和圆相切，直线和圆相离，d5cm，cm≤，切线的判定定理等内容，欢迎下载使用。

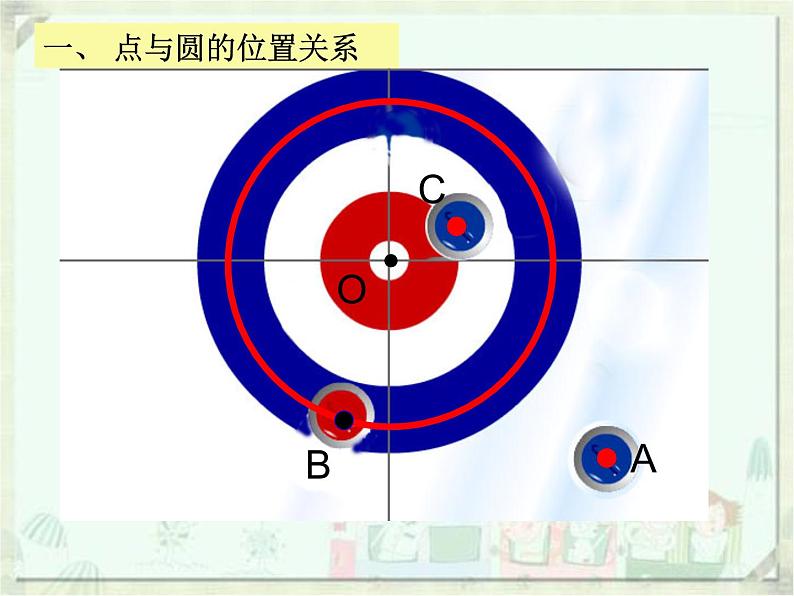
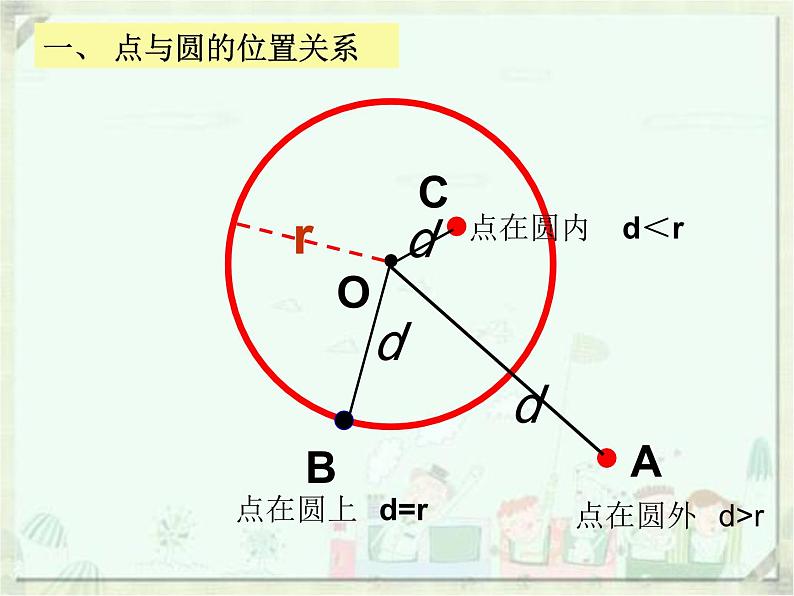
一、 点与圆的位置关系
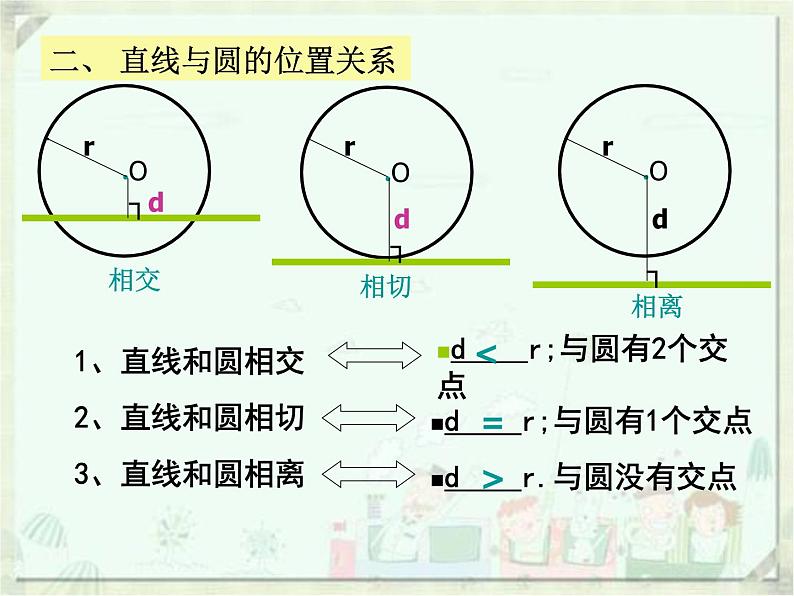
二、 直线与圆的位置关系
三、 圆与圆的位置关系
d r;与圆有1个交点
d r;与圆有2个交点
d r.与圆没有交点
定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.
　如图　∵OA是⊙O的半径, 且CD⊥OA, ∴ CD是⊙O的切线.
例2、判断直线l是否是⊙O的切线？并说明为什么。
如图, △ABC,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E．　　求证:DE是圆O的切线.
∵ 点O,点D分别是AB,AC的中点 ∴ OD是△ABC中位线 ∴ OD∥BC ∵ DE⊥BC ∴ ∠CED=∠ODE=90° ∴ OD⊥DE ∴ DE是圆O的切线
(提示：连接OD,则OD是△ABC的中位线,证OD⊥DE)
在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为圆心,DB为半径作⊙D. 求证:AC是⊙D的切线.
过点D作DF ⊥ AC与点F
∴∠AFD=∠ABD=90°∵∠A的平分线交BC于D∴BD=DF∴AC是⊙D的切线
(提示：过点D作DF ⊥ AC)
切线的判定定理的两种应用
1、连半径，证垂直 如果已知直线与圆有交点，往往要作出过这一点的半径，再证明直线垂直于这条半径即可.2、作垂线，证半径 如果不明确直线与圆的交点，往往要作出圆心到直线的垂线段，再证明这条垂线段等于半径即可.
圆的切线垂直于过切点的半径.
　　∵CD切⊙O于Ａ, A是切点, OA是⊙O的半径
提示：切线的性质定理是证明两条直线垂直的重要根据;作过切点的半径是常用经验辅助线之一.
按图填空：(1). 如果AB是⊙O的切线，那么
(3).如果AB是⊙O的切线，OA⊥AB，那么A是______
从圆外一点可以引圆的两条切线，他们的切线长___________ ，这一点和圆心的连线会__________两条切线的夹角
∵PA,PB切⊙O于A,B ∴ ___________ ____________
已知：如图,PA、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA=12CM，求△PEF的周长。
易证EQ=EA, FQ=FB, PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
同心圆是内含的特殊情况
如图， ⊙O的半径为 cm，正三角形的边长为10 cm，圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动，设运动时间为t（s）问:（1） 在移动过程中， ⊙O与△ABC 的三条边相切几次？ （2） t为何值时， ⊙O与 AC相切？
探究 如图， ⊙O的半径为 cm，正三角形的边长为10 cm，圆心O从B开始沿折线B-A-C-B以2 cm/s的速度移动，设运动时间为t（s）问： （1） 在移动过程中， ⊙O与△ABC 的三条边相切几次？ （2） t为何值时， ⊙O与 AC相切？
解（1） 在移动过程中， ⊙O与△ABC 的三条边相切6次。
（2）① 当圆心O在_____上时
（①当圆心O在BA上时有两次；②当圆心O在AC上时有两次；③当圆心O在CB上时有两次）
②当圆心O在_____上时
（①当圆心O在BA上时有两次；②当圆心O在AC上时有两次；③当圆心O在BC上时有两次）
（2）① 当圆心O在AB上时
∵ OD=r= 时⊙O与 AC相切
∵ Rt△AOD中∠ A=60°∴ ∠ AOD=30°
设AD=x ， AO=2AD=2x
∴AD=1 ， AO=2
∴t=8 2=4s时，⊙O与 AC相切
作OD⊥ AC于D
∵ OD=r= 时⊙O与 AC相切
设AD=x ， AO=2AD=2x
∴t=8 2=4s时，⊙O与 AC相切
作OE⊥ AC于E
∵ OE=r= 时⊙O与 AC相切
此时，得CO=AO=2
∴t=22 2=11s时，⊙O与 AC相切
点O移动距离为22
∴t = 4s 或 11s 时， ⊙O与 AC相切
1.点和圆三种的位置关系
2.直线和圆三种的位置关系
3.圆和圆五种的位置关系
（1）点在圆上；（2）点在圆外；（3）点在圆内
（1）相离；（2）相切；（3）相交（A）切线的性质及其判定；（B）切线长定理
（1）外离；（2）外切；（3）相交；（4）内切；（5）内含