2023-2024学年张掖市重点中学数学八年级第一学期期末检测试题含答案

这是一份2023-2024学年张掖市重点中学数学八年级第一学期期末检测试题含答案，共8页。试卷主要包含了下列各式计算结果是的是，解分式方程，可得分式方程的解为，下列四个命题中，真命题有等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1．如图，在△ABC中，AB = AC，∠A = 40º，DE垂直平分AC，则∠BCD的度数等于（ ）
A．20ºB．30º
C．40ºD．50º
2．如图，在△ABC中，∠BAC＝90°，AD是△ABC的高，若∠B＝20°，则∠DAC＝（ ）
A．90°B．20°C．45°D．70°
3．下列计算正确的是（ ）
A．a6÷a2=a3B．（a3）2=a5
C．D．
4．下列各式计算结果是的是（ ）
A．B．C．D．
5．解分式方程，可得分式方程的解为（ ）
A．B．C．D．无解
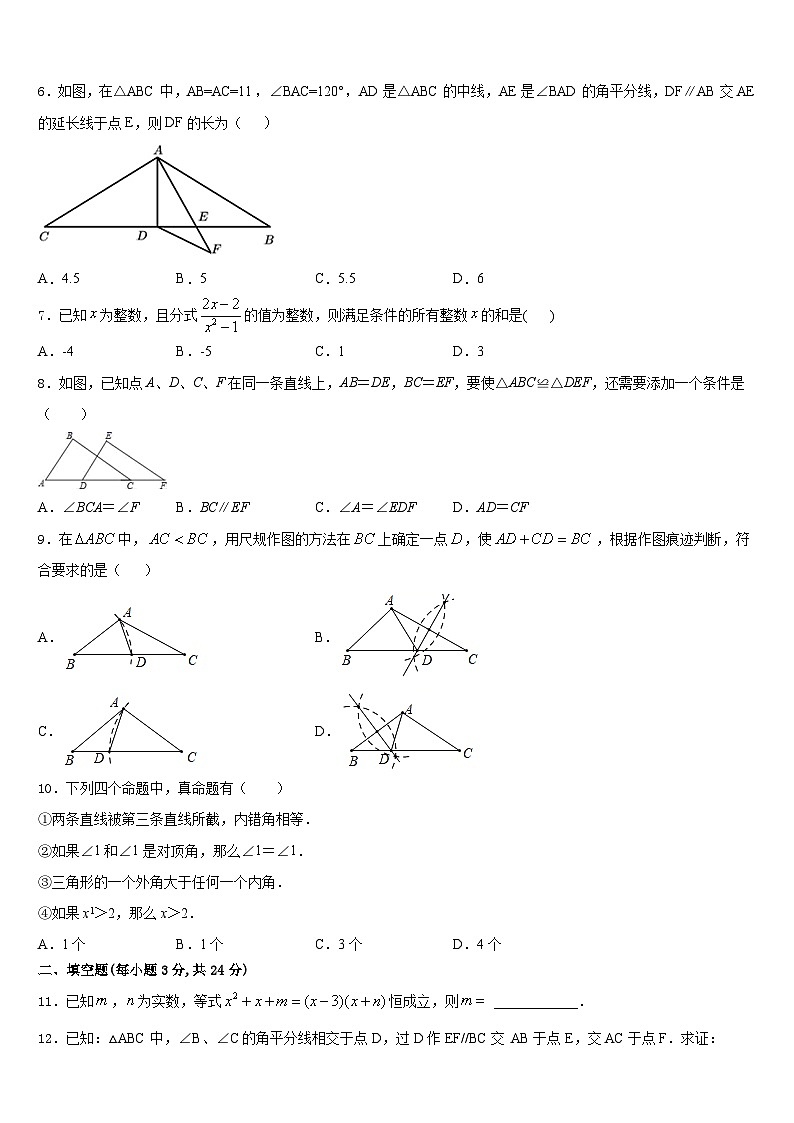
6．如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点E，则DF的长为（ ）
A．4.5B．5C．5.5D．6
7．已知为整数，且分式的值为整数，则满足条件的所有整数的和是( )
A．-4B．-5C．1D．3
8．如图，已知点A、D、C、F在同一条直线上，AB＝DE，BC＝EF，要使△ABC≌△DEF，还需要添加一个条件是（ ）
A．∠BCA＝∠FB．BC∥EFC．∠A＝∠EDFD．AD＝CF
9．在中，，用尺规作图的方法在上确定一点，使，根据作图痕迹判断，符合要求的是（ ）
A．B．
C．D．
10．下列四个命题中，真命题有（ ）
①两条直线被第三条直线所截，内错角相等．
②如果∠1和∠1是对顶角，那么∠1＝∠1．
③三角形的一个外角大于任何一个内角．
④如果x1＞2，那么x＞2．
A．1个B．1个C．3个D．4个
二、填空题(每小题3分,共24分)
11．已知，为实数，等式恒成立，则 ____________．
12．已知：△ABC中，∠B、∠C的角平分线相交于点D，过D作EF//BC交 AB于点E，交AC于点F．求证：BE+CF=EF．
13．如图，△ABE和△ACD是△ABC分别沿着AB、AC翻折而成的，若∠1=140°，∠2=25°，则∠α度数为______．
14．如果一个多边形的内角和为1260°，那么从这个多边形的一个顶点出发共有________条对角线．
15．如图，在正方形网格中有两个小正方形被涂黑，再涂黑一个图中其余的小正方形，使得整个被涂黑的图案构成一个轴对称图形，那么涂法共有_____种．
16．分解因式：_________．
17．如图，中，点在上，点在上，点在的延长线上，且，若，则的度数是________．
18．如图，中，、的平分线交于点，，则________．
三、解答题(共66分)
19．（10分）某服装店用4400元购进A，B两种新式服装，按标价售出后可获得毛利润2800元（毛利润＝售价﹣进价），这两种服装的进价，标价如表所示．
（1）请利用二元一次方程组求这两种服装各购进的件数；
（2）如果A种服装按标价的9折出售，B种服装按标价的8折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？
20．（6分）已知一次函数，它的图像经过，两点．
（1）求与之间的函数关系式；
（2）若点在这个函数图像上，求的值．
21．（6分）（1）
（2）解方程组：
22．（8分）2019年是中国建国70周年，作为新时期的青少年，我们应该肩负起实现祖国伟大复兴的责任，为了培养学生的爱国主义情怀，我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学，已知学生的人数是老师人数的12倍多20人，学生和老师总人数有540人．
（1）请求出去抗日战争纪念馆研学的学生和老师的人数各是多少？
（2）如果学校准备租赁型车和型车共14辆（其中型车最多7辆），已知型车每年最车可以载35人，型车每车最多可以载45人，共有几种租车方案？
（3）已知型车日租金为2000元，型车日租金为3000元，设租赁型大巴车辆，求出租赁总租金为元与的函数解析式，并求出最经济的租车方案．
23．（8分）如图，在等边中，线段为边上的中线．动点在直线上时，以为一边在的下方作等边，连结．
（1）求的度数；
（2）若点在线段上时，求证：；
（3）当动点在直线上时，设直线与直线的交点为，试判断是否为定值？并说明理由．
24．（8分）小明和小华加工同一种零件，己知小明比小华每小时多加工15个零件，小明加工300个零件所用时间与小华加工200个零件所用的时间相同，求小明每小时加工零件的个数.
25．（10分）已知点A（0，4）、C（﹣2，0）在直线l：y＝kx+b上，l和函数y＝﹣4x+a的图象交于点B
（1）求直线l的表达式；
（2）若点B的横坐标是1，求关于x、y的方程组的解及a的值．
（3）若点A关于x轴的对称点为P，求△PBC的面积．
26．（10分）在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题．
材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的．
例：已知：，求代数式x2+的值．
解：∵，∴＝4
即＝4∴x+＝4∴x2+＝（x+）2﹣2＝16﹣2＝14
材料二：在解决某些连等式问题时，通常可以引入参数“k”，将连等式变成几个值为k的等式，这样就可以通过适当变形解决问题．
例：若2x＝3y＝4z，且xyz≠0，求的值．
解：令2x＝3y＝4z＝k（k≠0）
则
根据材料回答问题：
（1）已知，求x+的值．
（2）已知，（abc≠0），求的值．
（3）若，x≠0，y≠0，z≠0，且abc＝7，求xyz的值．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、D
4、B
5、D
6、C
7、B
8、D
9、D
10、A
二、填空题(每小题3分,共24分)
11、－12
12、证明见解析
13、80°
14、1
15、1
16、
17、70°
18、72°
三、解答题(共66分)
19、（1) 购A型50件，B型30件．（2) 2440元．
20、 (1) ;(2).
21、（1）；（2）
22、（1）去抗日战争纪念馆研学的学生有500人，老师有40人；（2）3；（3）租赁A型大巴车9辆和租赁B型大巴车5辆．
23、（1）30°；（2）证明见解析；（3）是定值，.
24、45
25、（1）y＝2x+4（2）x=1,y=6; a=10（3）1
26、（1）5；
（2）；
（3）
类型价格
A型
B型
进价（元/件）
60
100
标价（元/件）
100
160