内蒙古自治区巴彦淖尔市磴口县实验中学2023-2024学年九年级上学期期中数学试题

这是一份内蒙古自治区巴彦淖尔市磴口县实验中学2023-2024学年九年级上学期期中数学试题，共11页。试卷主要包含了11等内容，欢迎下载使用。
（考试时间：90分钟，满分120分）
一、选择题（本大题共10小题，每小题3分，共30分）
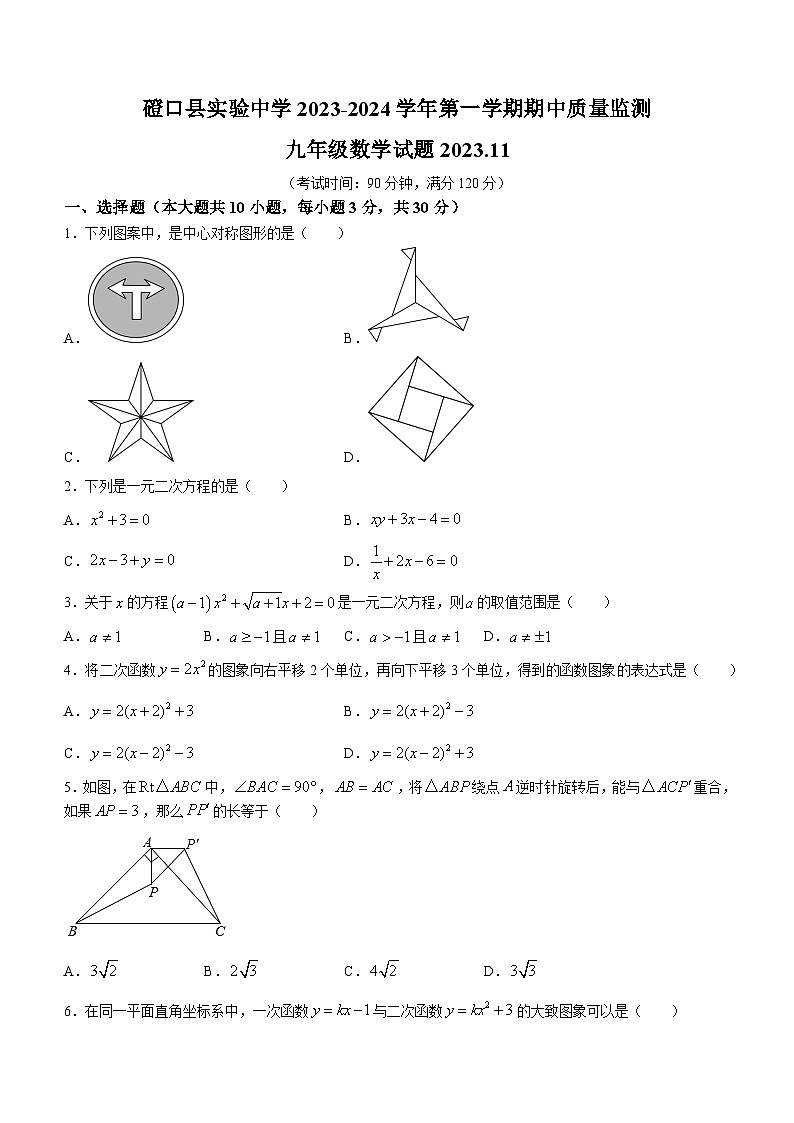
1．下列图案中，是中心对称图形的是（ ）
A．B．
C．D．
2．下列是一元二次方程的是（ ）
A．B．
C．D．
3．关于的方程是一元二次方程，则的取值范围是（ ）
A．B．且C．且D．
4．将二次函数的图象向右平移2个单位，再向下平移3个单位，得到的函数图象的表达式是（ ）
A．B．
C．D．
5．如图，在中，，，将绕点逆时针旋转后，能与重合，如果，那么的长等于（ ）
A．B．C．D．
6．在同一平面直角坐标系中，一次函数与二次函数的大致图象可以是（ ）
A．B．
C．D．
7．三角形两边长分别为2和3，第三边的长是方程的根，则该三角形的周长为（ ）
A．B．10C．D．或10
8．如图，在中，以点为中心，将顺时针旋转30°得到，边，相交于点，，则的度数为（ ）
A．35°B．30°C．65°D．60°
9．如图，抛物线与轴交于点和，与轴交于点．下列结论：①，②，③，④，其中正确的结论个数为（ ）
A．1个B．2个C．3个D．4个
10．（3分）如图，有一张矩形纸条，，，点M，N分别在边，上，．现将四边形沿折叠，使点B，C分别落在点，上．当点恰好落在边上时，下列结论不一定正确的是（ ）
A．B．C．D．
二、填空题（每小题3分共24分）
11．中国“一带一路”给沿线国家和地区带来很大的经济效益，沿线某地区居民2016年人均年收入20000元，到2018年人均年收入达到39200元．则该地区居民年人均收入平均增长率为________．（用百分数表示）
12．方程的根为________．
13．设a，b是方程的两个实数根，则的值为________．
14．对于实数a，b，我们定义一种新的运算#，规定：，若关于x的方程的一个实数根为4，则________．
15．已知函数是二次函数，则常数m的取值范围是________．
16．若点关于原点对称的点是第一象限的点，则a的取值范围是________．
17．如图，若点B的坐标为，则点A的坐标为________．
18．如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，当水面宽度为时，拱顶离水面________m．
三、计算题（本大题共6小题，共66分）
19．解方程：（本大题共3小题，共15分）
（1）（用配方法解）；（2）（3）；
20．（8分）如图，在中，，将绕点A逆时针旋转到的位置，使得．
（1）请判断的形状，并说明理由．
（2）求的度数．
21．（8分）如图，东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园，矩形的一边用教学楼的外墙，其余三边用竹篱笆．设矩形的宽为x米，面积为y平方米．
（1）求y与x的函数关系式．
（2）怎样设计矩形地块的长和宽，面积最大？并求最大面积．
22．（10分）某商场品牌童装每件进价60元，售价100元，平均每天可售出20件，为了迎接“元旦”商场采取了促销活动，增加盈利，尽快减少库存，经市场调查，若每件童装降价1元，平均每天就可多售出2件．
（1）不搞促销活动时，每件童装可盈利多少元？
（2）要使某商场每天盈利1200元，那么每件童装应降价多少元？
（3）该商品销售单价应定为多少元时，获得利润最大，最大利润为多少元？
23．（11分）如图，三个顶点的坐标分别是，，．
（1）请画出向左平移5个单位长度后得到的；
（2）请画出关于原点对称的；
（3）在轴上求作一点，使周长最小，请画出，并直接写出点的坐标，并求周长的最小值．
24．（14分）如图，在平面直角坐标系中，已知抛物线与轴交于A，B两点，与y轴交于点C，直线经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接，已知点A，D的坐标分别为，．
（1）求抛物线的函数表达式，并分别求出点B和点E的坐标；
（2）试探究抛物线上是否存在点F，使，若存在，请直接写出点F的坐标；若不存在，请说明理由；
（3）若点P是y轴负半轴上的一个动点，设其坐标为．试探究：当m为何值时，是等腰三角形．
磴口县实验中学2023-2024学年第一学期期中质量监测
九年级数学试题答题纸2023.11
（考试时间：90分钟，满分120分）
一、选择题（本大题共10小题，每小题3分，共30分）
二、填空题（本大题共8小题，每小题3分，共24分）
11．40%12．，13．202214．3
15．16．17．18．4
三、解答题（共66分）
19．（15分）（1），
，
，
，
，
或，
，．
（2）
或
，
（3）
．
20．（8分）（1）是等腰三角形，理由如下：
∵将绕点逆时针旋转到的位置，
∴，
∴是等腰三角形；
（2），
∴，
∵，
∴，
∴，
∵将绕点逆时针旋转到的位置，
∴．
21．（8分）
（1）设矩形的宽为米，则长为米，
∴，
∴与的函数关系式为；
（2）∵
∵矩形的宽为米，长为米，
∴，
解得：
∴，
∵，
∴当时，有最大值，最大值为200，此时，
∴矩形地块的长为20米，宽为10米时，面积最大，最大面积为200平方米．
22．（10分）
（1）不搞促销活动时，每件童装可盈利（元）；
（2）设每件童装应降价元，则
，
即：，
解得：，，
∵尽快减少库存，
∴舍去．
答：每件童装应降价20元．
（3）略
23．（11分）（1）如图，即为所求；
（2）如图，即为所求；
（3）如图，即为所求，点P的坐标是，
∵，
∴周长的最小值
24．（14分）
（1）∵抛物线经过点
∴，
∴，解得
∴抛物线解析式为；
（2）抛物线上存在点使得，
设直线的解析式为，
∵经过点，
∴，
∴，
∴直线的解析式为，
∵，
∴抛物线对称轴为直线，
∵点为直线与抛物线对称轴的交点，
点的横坐标为3，纵坐标为，
∴点坐标，
由点，点，点的坐标，可知，
与有公共边，
此时点纵坐标为，
∴，
∴，
解得：，
∴点坐标或
（3）①如图1中，当时，是等腰三角形，
图1
∵点坐标，，
过点作直线，交轴于点，交轴于点．
则，
∴，
∴点坐标．
设直线的解析式为，
∴，
∴，
∴直线解析式为，
令，得，解得，
∴点坐标，
∵，
∴，即，，
②如图2中，当时，是等腰三角形．
图2
∵当时，，
∴点坐标，
∴，
∴，
∴，，
∴，
∴，
∴，
设直线交轴于，解析式为，
∴，
∴，
∴直线解析式为，
令，得，
∴，
∴点坐标，
∵，
∴，
∴，
∴．
③时，显然不可能，
综上所述，当或时，是等腰三角形．
题号
1
2
3
4
5
6
7
8
9
10
选项
D
A
B
C
A
C
A
B
B
D