2023-2024学年湖南省师范大附属中学八上数学期末监测试题含答案

这是一份2023-2024学年湖南省师范大附属中学八上数学期末监测试题含答案，共9页。试卷主要包含了不等式3，化简的结果是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．下列说法正确的是（ ）
A．计算两个班同学数学成绩的平均分，可以用两个班的平均分除以2即可；
B．10，9，10，12，11，12这组数据的众数是10；
C．若，，，…，的平均数是，那么
D．若，，，…，的方差是，那么，，，…方差是．
2．某市道路改造中，需要铺设一条长为1200米的管道，为了尽量减少施工对交通造成的影响，实际施工时，工作效率比原计划提高了25%，结果提前了8天完成任务．设原计划每天铺设管道x米，根据题意，则下列方程正确的是（ ）
A． B．
C．D．
3．在解分式方程时，我们第一步通常是去分母，即方程两边同乘以最简公分母（x﹣1），把分式方程变形为整式方程求解．解决这个问题的方法用到的数学思想是（ ）
A．数形结合B．转化思想C．模型思想D．特殊到一般
4．某小区开展“节约用水，从我做起”活动，下表是从该小区抽取的10个家庭本月与上月相比节水情况统计表：
这10个家庭节水量的平均数和中位数分别是（ ）
A．0.42和0.4B．0.4和0.4C．0.42和0.45D．0.4和0.45
5．下列各组数可能是一个三角形的边长的是（ ）
A．5，7，12B．5，6，7C．5，5，12D．1，2，6
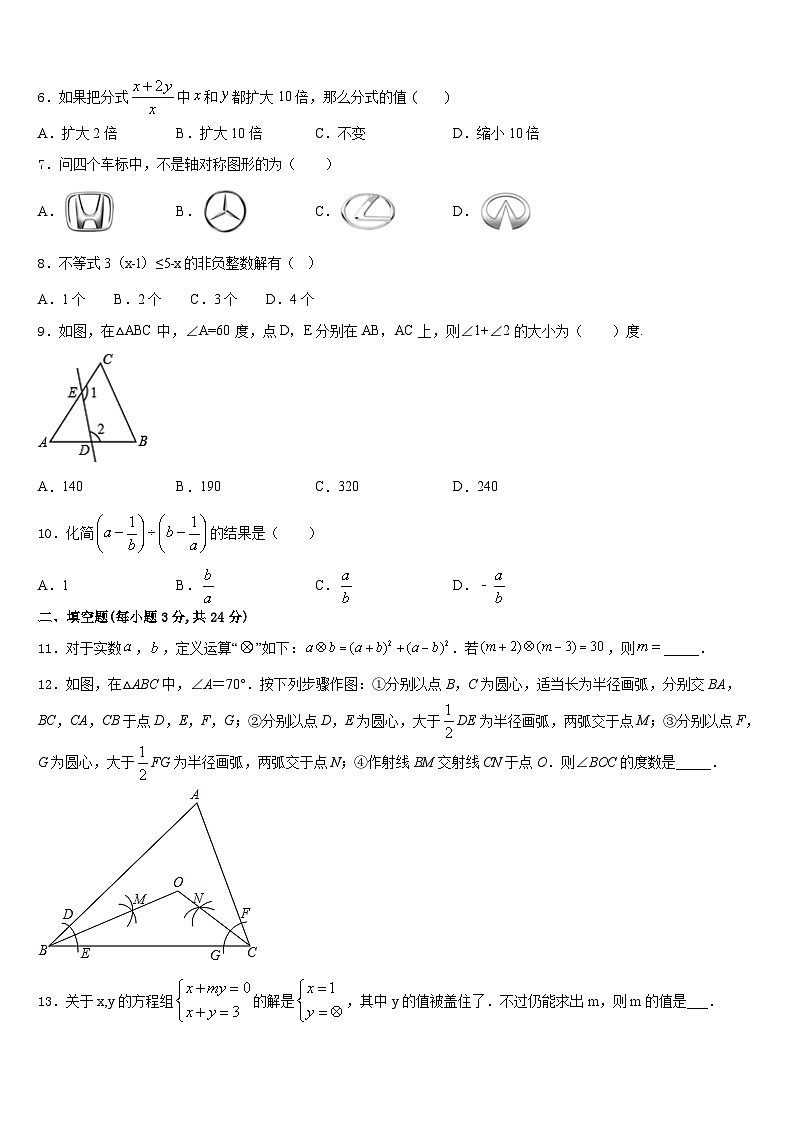
6．如果把分式中和都扩大10倍，那么分式的值 ( )
A．扩大2倍B．扩大10倍C．不变D．缩小10倍
7．问四个车标中，不是轴对称图形的为（ ）
A．B．C．D．
8．不等式3（x﹣1）≤5﹣x的非负整数解有（ ）
A．1个 B．2个 C．3个 D．4个
9．如图，在△ABC中，∠A=60度，点D，E分别在AB，AC上，则∠1+∠2的大小为（ ）度.
A．140B．190C．320D．240
10．化简的结果是（ ）
A．1B．C．D．﹣
二、填空题(每小题3分,共24分)
11．对于实数，，定义运算“”如下：．若，则_____．
12．如图，在△ABC中，∠A＝70°．按下列步骤作图：①分别以点B，C为圆心，适当长为半径画弧，分别交BA，BC，CA，CB于点D，E，F，G；②分别以点D，E为圆心，大于DE为半径画弧，两弧交于点M；③分别以点F，G为圆心，大于FG为半径画弧，两弧交于点N；④作射线BM交射线CN于点O．则∠BOC的度数是_____．
13．关于x,y的方程组的解是，其中y的值被盖住了．不过仍能求出m，则m的值是___．
14．如图，在平面直角坐标系中，有一个正三角形，其中，的坐标分别为和．若在无滑动的情况下，将这个正三角形沿着轴向右滚动，则在滚动过程中，这个正三角形的顶点，，中，会过点的是点__________．
15．的3倍与2的差不小于1，用不等式表示为_________．
16．已知的两条边长分别为4和8，第三边的长为，则的取值范围______．
17．小明同学在百度搜索引擎中输入“中国梦，我的梦”，引擎搜索耗时0.00175秒，将这个数用科学记数法表示为____．
18．纳米是一种长度单位，1纳米=米，已知某种植物花粉的直径约为46 000纳米，用科学记数法表示表示该种花粉的直径为____________米．
三、解答题(共66分)
19．（10分）教材呈现：下图是华师版八年级上册数学教材第94页的部分内容．
定理证明：请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．
定理应用：
（1）如图②，在中，直线分别是边的垂直平分线，直线m、n交于点，过点作于点．
求证：．
（1）如图③，在中，，边的垂直平分线交于点，边的垂直平分线交于点．若，则的长为__________．
20．（6分）小山同学结合学习一次函数的经验和自己的思考，按以下方式探究函数的图象与性质，并尝试解决相关问题．
请将以下过程补充完整：
（1）判断这个函数的自变量x的取值范围是________________；
（2）补全表格：
（3）在平面直角坐标系中画出函数的图象：
（4）填空：当时，相应的函数解析式为___（用不含绝对值符合的式子表示）；
（5）写出直线与函数的图象的交点坐标．
21．（6分）下面是某同学对多项式（x2-4x+2）（x2-4x+6）+4进行因式分解的过程．
解：设x2-4x=y，
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2-4x+4）2（第四步）
（1）该同学第二步到第三步运用了因式分解的______．
A．提取公因式
B．平方差公式
C．两数和的完全平方公式
D．两数差的完全平方公式
（2）该同学因式分解的结果是否彻底？______．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果______．
（3）请你模仿以上方法尝试对多项式（x2-2x）（x2-2x+2）+1进行因式分解．
22．（8分）我市为创建省文明卫生城市，计划将城市道路两旁的人行道进行改造，经调查可知，若该工程由甲工程队单独来做恰好在规定时间内完成；若该工程由乙工程队单独完成，则需要的天数是规定时间的2倍，若甲、乙两工程队合作8天后，余下的工程由甲工程队单独来做还需3天完成．
（1）问我市要求完成这项工程规定的时间是多少天？
（2）已知甲工程队做一天需付给工资5万元，乙工程队做一天需付给工资2万元．两个工程队在完成这项工程后，共获得工程工资款总额65万元，请问该工程甲、乙两工程队各做了多少天？
23．（8分）为响应国家的号召，减少污染，某厂家生产出一种节能又环保的油电混合动力汽车，既可以用油做动力行驶，也可以用电做动力行驶．这种油电混合动力汽车从甲地行驶到乙地，若完全用油做动力行驶，费用为118元；若完全用电做动力行驶，费用为36元，已知汽车行驶中每千米用油的费用比用电的费用多1．6元．
（1）求汽车行驶中每千米用电的费用和甲、乙两地之间的距离．
（2）若汽车从甲地到乙地采用油电混合动力行驶，且所需费用不超过61元，则至少需要用电行驶多少千米？
24．（8分）（1）如图，已知的顶点在正方形方格点上每个小正方形的边长为1．写出各顶点的坐标
（2）画出关于y轴的对称图形
25．（10分）解方程组：
（1）
（2）．
26．（10分）一辆货车从甲地匀速驶往乙地，到达乙地停留一段时间后，沿原路以原速返回甲地．货车出发一段时间后，一辆轿车以的速度从甲地匀速驶往乙地．货车出发时，两车在距离甲地处相遇，货车回到甲地的同时轿车也到达乙地．货车离甲地的距离、轿车离甲地的距离分别与货车所用时间之间的函数图像如图所示．

（1）货车的速度是______，的值是______，甲、乙两地相距______；
（2）图中点表示的实际意义是：______．
（3）求与的函数表达式，并求出的值；
（4）直接写出货车在乙地停留的时间．
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、B
4、C
5、B
6、C
7、C
8、C
9、D
10、C
二、填空题(每小题3分,共24分)
11、
12、125°
13、
14、C
15、
16、4＜＜1
17、
18、4.6×10-1
三、解答题(共66分)
19、证明见解析；（1）证明见解析；（1）2．
20、（1）全体实数；（2）见解析；（3）见解析；（4）；（5）
21、（1）C；（2）不彻底，（x-2）1；（3）（x-1）1
22、（1）15天；（2）甲工程队做了5天，乙工程队做了20天
23、（1）汽车行驶中每千米用电的费用是元，甲、乙两地之间的距离是121千米；（2）至少需要用电行驶81千米．
24、（1）A（-2，2），B（-3，-1），C（-1，1）；（2）见解析
25、（1）；（2）
26、（1） 80；9；400 ；（2）货车出发后，轿车与货车在距甲地处相遇；（3） ；（4）货车在乙地停留．
节水量（）
0.2
0.3
0.4
0.5
0.6
家庭数（个）
1
2
2
4
1
1．线段垂直平分线
我们已经知道线段是轴对称图形，线段的垂直平分线是线段的对称轴，如图，直线是线段的垂直平分线，是上任一点，连结．将线段沿直线对折，我们发现与完全重合．由此即有：
线段垂直平分线的性质定理线段垂直平分线上的点到线段两端的距离相等．
已知：如图，垂足为点，点是直线上的任意一点．
求证：．
分析图中有两个直角三角形和，只要证明这两个三角形全等，便可证得．