2023-2024学年甘肃省兰州市数学八年级第一学期期末学业质量监测试题含答案

这是一份2023-2024学年甘肃省兰州市数学八年级第一学期期末学业质量监测试题含答案，共9页。
学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
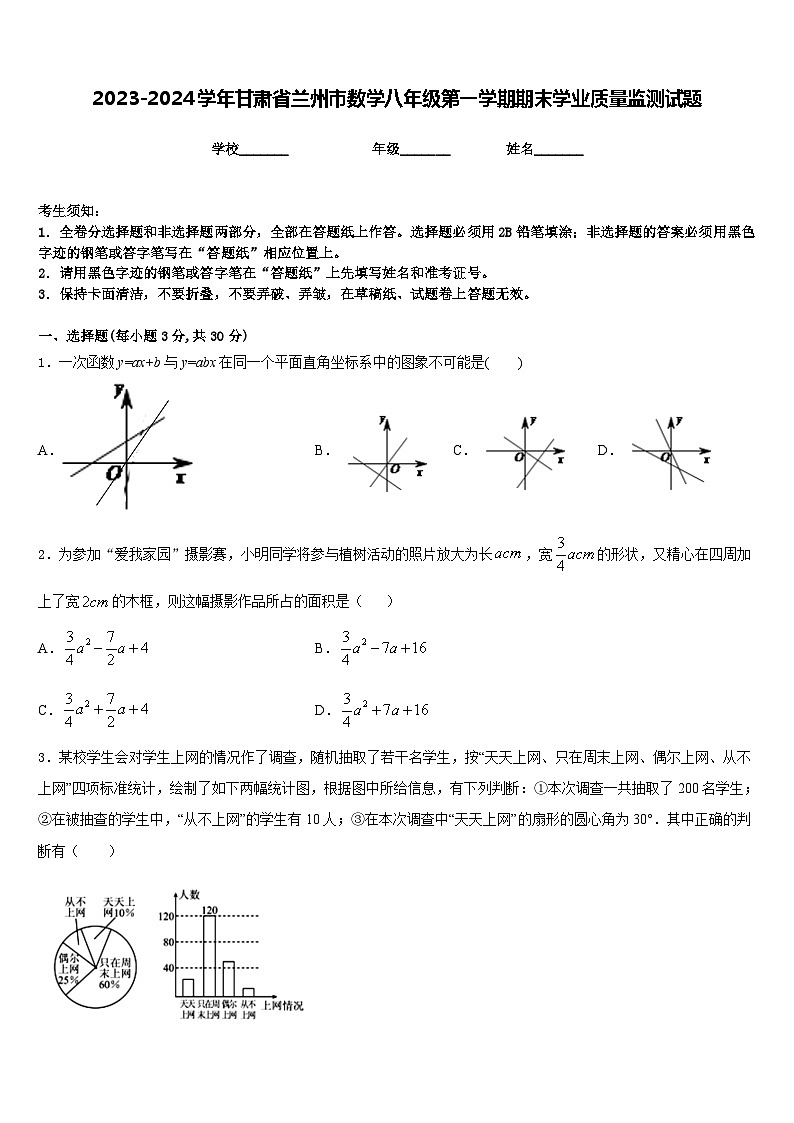
1．一次函数y=ax+b与y=abx在同一个平面直角坐标系中的图象不可能是( )
A．B．C．D．
2．为参加“爱我家园”摄影赛，小明同学将参与植树活动的照片放大为长，宽的形状，又精心在四周加上了宽的木框，则这幅摄影作品所占的面积是（ ）
A．B．
C．D．
3．某校学生会对学生上网的情况作了调查，随机抽取了若干名学生，按“天天上网、只在周末上网、偶尔上网、从不上网”四项标准统计，绘制了如下两幅统计图，根据图中所给信息，有下列判断：①本次调查一共抽取了200名学生；②在被抽查的学生中，“从不上网”的学生有10人；③在本次调查中“天天上网”的扇形的圆心角为30°．其中正确的判断有（ ）
A．0个B．1个C．2个D．3个
4．两张长方形纸片按如图所示的方式叠放在一起，则图中相等的角是（ ）
A．与B．与C．与D．三个角都相等
5．如果某多边形的每个内角的大小都是其相邻外角的3倍，那么这个多边形是（ ）
A．六边形B．八边形C．正六边形D．正八边形
6．如图，在△ABC，∠C＝90°，AD平分∠BAC交CB于点D，过点D作DE⊥AB，垂足恰好是边AB的中点E，若AD＝3cm，则BE的长为（ ）
A．cmB．4cmC．3cmD．6cm
7．江永女书诞生于宋朝，是世界上唯一一种女性文字，主要书写在精制布面、扇面、布帕等物品上，是一种独特而神奇的文化现象．下列四个文字依次为某女书传人书写的“女书文化”四个字，基本是轴对称图形的是( )
A．
B．
C．
D．
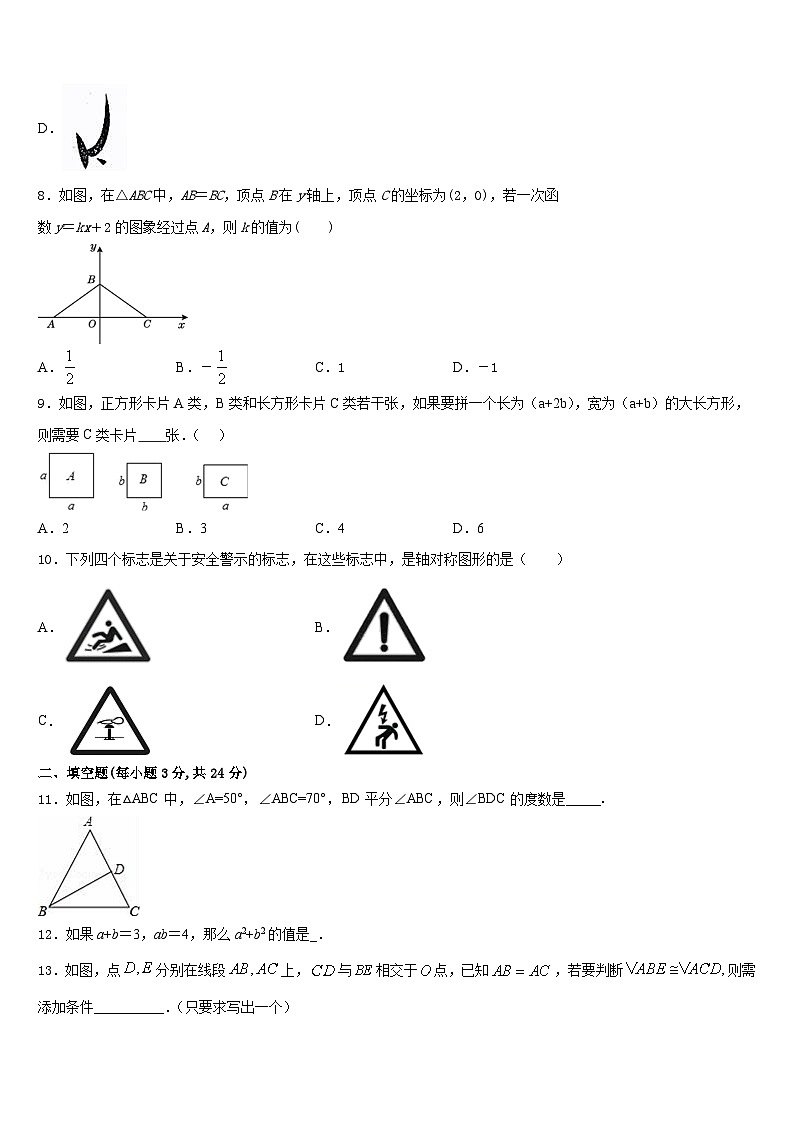
8．如图，在△ABC中，AB＝BC，顶点B在y轴上，顶点C的坐标为(2，0)，若一次函
数y＝kx＋2的图象经过点A，则k的值为( )
A．B．－C．1D．－1
9．如图，正方形卡片A类，B类和长方形卡片C类若干张，如果要拼一个长为（a+2b），宽为（a+b）的大长方形，则需要C类卡片 张．（ ）
A．2B．3C．4D．6
10．下列四个标志是关于安全警示的标志，在这些标志中，是轴对称图形的是（ ）
A．B．
C．D．
二、填空题(每小题3分,共24分)
11．如图，在△ABC中，∠A=50°，∠ABC=70°，BD平分∠ABC，则∠BDC的度数是_____．
12．如果a+b＝3，ab＝4，那么a2+b2的值是_．
13．如图，点分别在线段上，与相交于点，已知，若要判断则需添加条件__________．（只要求写出一个）
14．如图，ΔABC与ΔA′B′C′关于直线l对称，则∠B的度数为____．
15．等腰三角形的一条高与一腰的夹角为40°，则等腰三角形的一个底角为_____．
16．如图，在长方形ABCD中，按以下步骤作图：①分别以点A和C为圆心，以大于AC的长为半径作弧，两弧相交于点M和N；②作直线MN交CD于点E．若DE=3，CE=5，则AD的长为__________.
17．计算的结果是___________
18．中，，，点为延长线上一点，与的平分线相交于点，则的度数为__________．
三、解答题(共66分)
19．（10分）如图，Rt△ABC中，∠ACB=90°，AC=BC，点D在斜边AB上，且AD=AC，过点B作BE⊥CD交直线CD于点E．
（1）求∠BCD的度数；
（2）求证：CD=2BE．
20．（6分）把两个含有角的直角三角板和如图放置，点在同一直线上，点在上，连接，，的延长线交于点．猜想与有怎样的关系？并说明理由．
21．（6分）在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.
（1）求每台电脑、每台电子白板各多少万元?
（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低.
22．（8分）阅读下面材料：
小明遇到这样一个问题：
如图1，在中，平分，．求证：
小明通过思考发现，可以通过“截长、补短”两种方法解决问题：
方法1：如图2，在上截取，使得，连接，可以得到全等三角形，进而解决问题
方法二：如图3，延长到点，使得，连接，可以得到等腰三角形，进而解决问题
（1）根据阅读材料，任选一种方法证明
（2）根据自己的解题经验或参考小明的方法，解决下面的问题：如图4，四边形中，是上一点，，，，探究、、之间的数量关系，并证明
23．（8分）如图，在由6个大小相同的小正方形组成的方格中，设每个小正方形的边长均为1.
（1）如图①，，，是三个格点（即小正方形的顶点），判断与的位置关系，并说明理由；
（2）如图②，连接三格和两格的对角线，求的度数（要求：画出示意图，并写出证明过程）.
24．（8分）八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．
（探究与发现）
（1）如图1，是的中线，延长至点，使，连接，写出图中全等的两个三角形______
（理解与应用）
（2）填空：如图2，是的中线，若，，设，则的取值范围是______．
（3）已知：如图3，是的中线，，点在的延长线上，，求证：．
25．（10分）阅读下面的解题过程，求的最小值．
解：∵=，
而，即最小值是0；
∴的最小值是5
依照上面解答过程，
（1）求的最小值；
（2）求的最大值．
26．（10分）如图，M、N两个村庄落在落在两条相交公路AO、BO内部，这两条公路的交点是O，现在要建立一所中学C，要求它到两个村庄的距离相等，到两条公路的距离也相等．试利用尺规找出中学的位置（保留作图痕迹，不写作法）．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、D
3、C
4、B
5、D
6、A
7、A
8、C
9、B
10、B
二、填空题(每小题3分,共24分)
11、85°．
12、1．
13、答案不唯一，如
14、100°
15、50°或65°或25°
16、1
17、
18、15°
三、解答题(共66分)
19、（1）22.5°；（2）见解析
20、AD=BE，AD⊥BE
21、（1）每台电脑0.5万元，每台电子白板1.5万元（2）见解析
22、（1）证明见解析；（2），证明见解析
23、（1），理由见解析；（2），理由见解析.
24、（1）；（2）；（3）见解析
25、（1）2019；（2）1．
26、作图见解析.