2023-2024学年衡水市重点中学数学八上期末学业质量监测模拟试题含答案

这是一份2023-2024学年衡水市重点中学数学八上期末学业质量监测模拟试题含答案，共7页。试卷主要包含了已知，如图所示，下列各数中，无理数的是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
1．已知，则M等于（ ）
A．B．C．D．
2．如图，在中，AB=8，BC=6，AB、BC边上的高CE、AD交于点H，则AD与CE的比值是（ ）
A．B．
C．D．
3．已知：如图，四边形中，，．在边上求作点，则的最小值为（ ）
A．B．C．D．
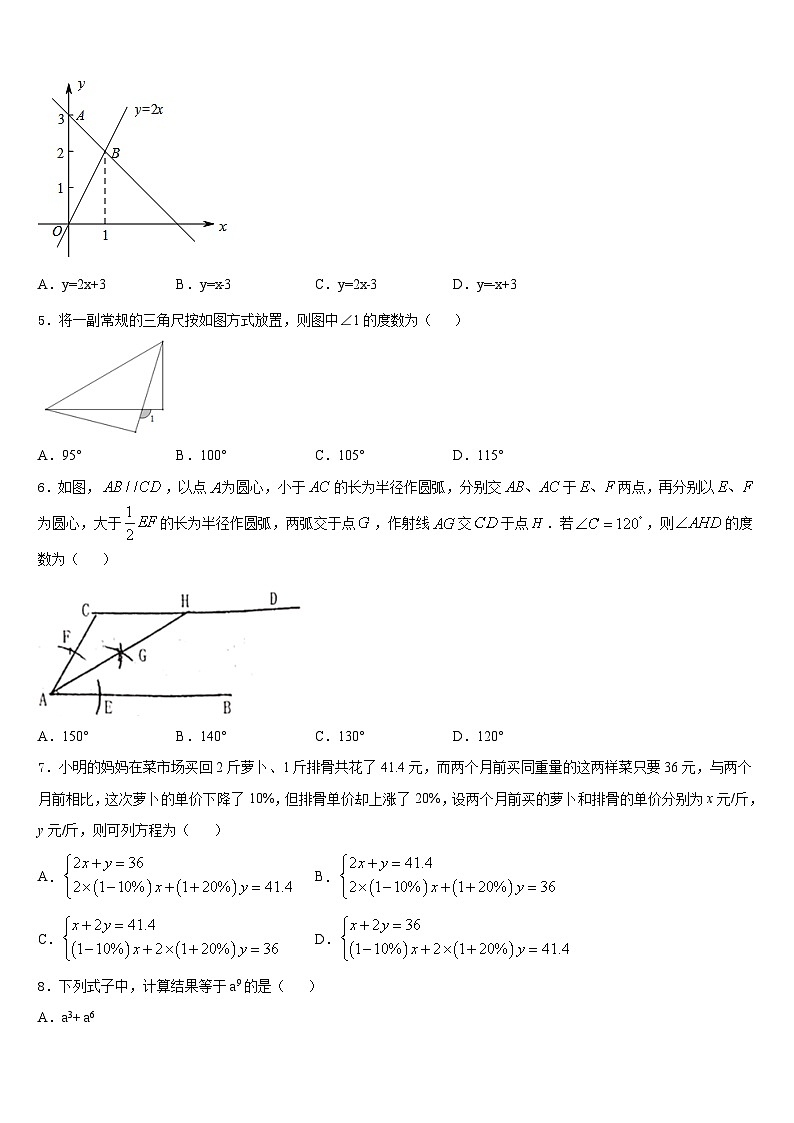
4．如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（ ）
A．y=2x+3B．y=x﹣3C．y=2x﹣3D．y=﹣x+3
5．将一副常规的三角尺按如图方式放置，则图中∠1的度数为（ ）
A．95°B．100°C．105°D．115°
6．如图，，以点为圆心，小于的长为半径作圆弧，分别交于两点，再分别以为圆心，大于的长为半径作圆弧，两弧交于点，作射线交于点．若，则的度数为（ ）
A．150°B．140°C．130°D．120°
7．小明的妈妈在菜市场买回2斤萝卜、1斤排骨共花了41.4元，而两个月前买同重量的这两样菜只要36元，与两个月前相比，这次萝卜的单价下降了10%，但排骨单价却上涨了20%，设两个月前买的萝卜和排骨的单价分别为x元/斤，y元/斤，则可列方程为（ ）
A．B．
C．D．
8．下列式子中，计算结果等于a9的是（ ）
A．a3+ a6
B．a1．a
C．(a6) 3
D．a12÷a2
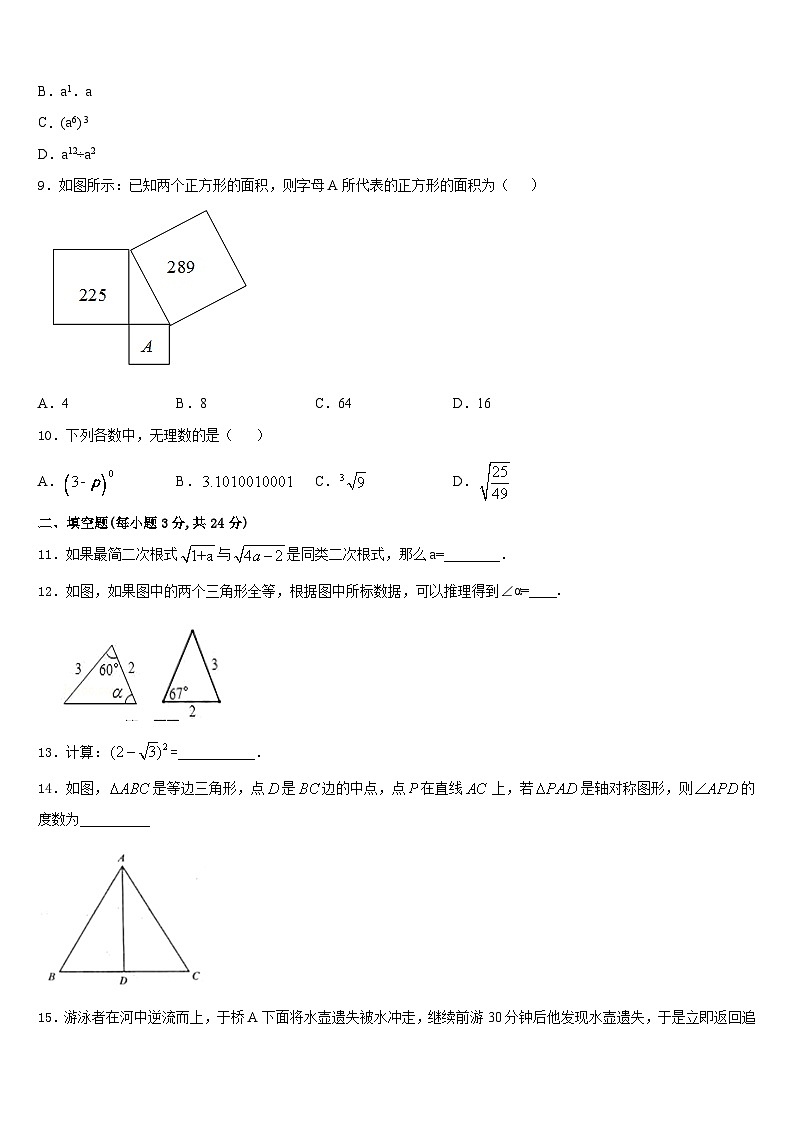
9．如图所示：已知两个正方形的面积，则字母A所代表的正方形的面积为（ ）
A．4B．8C．64D．16
10．下列各数中，无理数的是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．如果最简二次根式与是同类二次根式，那么a=________．
12．如图，如果图中的两个三角形全等，根据图中所标数据，可以推理得到∠α=____．
13．计算：=___________．
14．如图，是等边三角形，点是边的中点，点在直线上，若是轴对称图形，则的度数为__________
15．游泳者在河中逆流而上，于桥A下面将水壶遗失被水冲走，继续前游30分钟后他发现水壶遗失，于是立即返回追寻水壶，在桥A下游距桥1.2公里的桥B下面追到了水壶，那么该河水流的速度是_________．
16．A，B两地相距48千米，一艘轮船从A地顺流航行至B地，又立即从B地逆流返回A地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则可列方程____________．
17．因式分解：（a+b）2﹣64＝_____．
18．面试时，某人的基本知识、表达能力、工作态度的得分分别是80分、70分、85分，若依次按30%、30%、40%的比例确定成绩，则这个人的面试成绩是____________．
三、解答题(共66分)
19．（10分）已知：如图，在中，是的平分线交于点，垂足为.
(1)求证：.
(2)若，求的长.
20．（6分）先化简，再求值：b（b﹣2a）﹣（a﹣b）2，其中a＝﹣3，b＝﹣．
21．（6分）如图，是上一点，与交于点，，．线与有怎样的数量关系，证明你的结论．
22．（8分）如图，直线l1：y1=x和直线l2：y2=-2x+6相交于点A，直线l2与x轴交于点B，动点P沿路线O→A→B运动．
（1）求点A的坐标，并回答当x取何值时y1＞y2？
（2）求△AOB的面积；
（3）当△POB的面积是△AOB的面积的一半时，求出这时点P的坐标．
23．（8分）如图，已知，为线段上一点，为线段上一点，，设，．
①如果，那么_______，_________；
②求之间的关系式．
24．（8分）如图，已如是等边三角形，于点，于点，，求证：
（1）≌；
（2）是的垂直平分线．
25．（10分）过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE，CF．
（1）求证：四边形AECF是菱形；
（2）若AB＝6，AC＝10，EC＝，求EF的长．
26．（10分）八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．
（探究与发现）
（1）如图1，是的中线，延长至点，使，连接，写出图中全等的两个三角形______
（理解与应用）
（2）填空：如图2，是的中线，若，，设，则的取值范围是______．
（3）已知：如图3，是的中线，，点在的延长线上，，求证：．
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、B
4、D
5、C
6、A
7、A
8、B
9、C
10、C
二、填空题(每小题3分,共24分)
11、1
12、67°
13、7-4.
14、15°或30°或75°或120°
15、0.01km/min
16、
17、（a+b﹣8）（a+b+8）
18、79分
三、解答题(共66分)
19、 (1)证明见详解；(2)CD=2.
20、﹣a2，﹣1
21、,证明详见解析
22、（1）当x＞2时，y1＞y2；（2）3；（3）P（1，1）或（，1）．
23、①20，10；②α=2β
24、（1）见解析；（2）见解析
25、（1）证明见解析；（2）.
26、（1）；（2）；（3）见解析